Multiplicand|Definition & Meaning

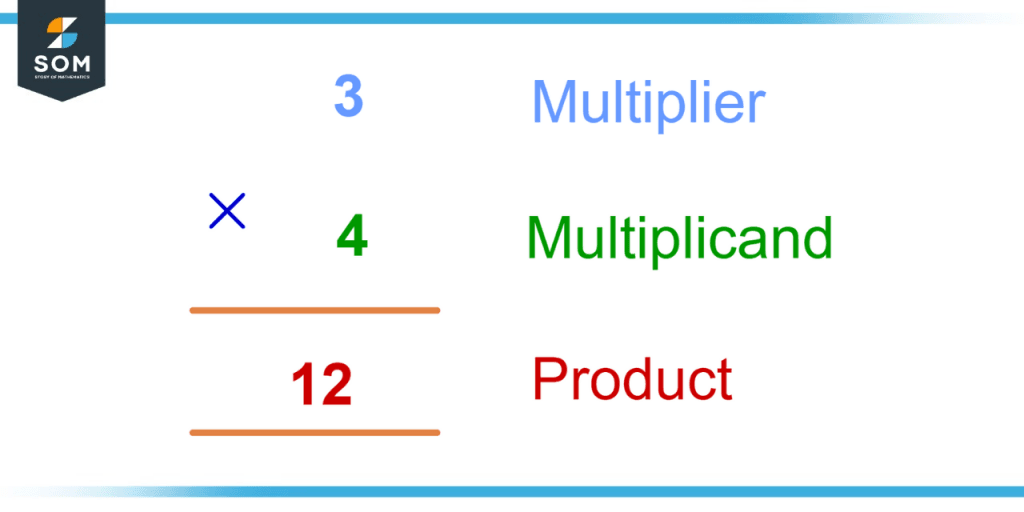
Figure 1: 4 is the multiplicand in the multiplication of 3 and 4. 

Let us take a deeper look into the operation of multiplication to get a better understanding of the multiplicand. 

Multiplication

Multiplication is one of the four fundamental arithmetic operations – the others being addition, subtraction, and division. Simply defined, multiplication is an extension of addition and represents the repeated addition of a number.  For example, the multiplication of 3 with 4 can be viewed as the addition of four threes. 

Multiplication can be performed between all the real numbers – integers, rational and irrational numbers – and complex numbers as well. Multiplication also exists for advanced mathematical structures such as matrices and sets. 

Notation

There are several notations of representing multiplication, some with special contexts, whereas others are used interchangeably.

• The most common notation used is the symbol $\times$ between the multiplier and the multiplicand called the multiplication sign. For example, 6 $\times$ 8. 
• Multiplication is also represented by the dot symbol between the operands in the middle position rather than the period. For example, 6 $\cdot$ 8. 
• Multiplication is mostly represented with an asterisk (*) symbol in computer programs. For example, 6 * 8. 
• It is also represented in the form of parentheses around the operands. For example, 6(8) or (6)(8) both represent the multiplication of 6 and 8. 
• Multiplication of variables is usually represented without any symbol and the variables are just written side by side. For example, the product of variables ‘a’ and ‘b’ would usually be written as ‘ab.’ Multiplication of a number with a variable is also written in the same way as the multiplication of ‘7’ and ‘y’ is written as ‘7y.’ 

Properties of Multiplication

Several common properties of multiplication are as follows:

• Commutative property holds for multiplication. This implies that the order of the operands has no effect on the resulting product. Formally, this is written as:

a + b = b + a

• Similar to the commutative property, associative property also holds for multiplication. By extension, multiplication is independent of order for any number of operands. 
• Multiplication is distributive over addition and subtraction. This is represented as:

a (b ± c) = ab ± ac 

• Multiplication of any number with 1 results in the product being equal to the same number. For this reason, 1 is called the identity element for multiplication. Formally:

x $\cdot$ 1 = x

• Multiplication of any number with 0 results in the product being equal to 0. This is written as:

x $\cdot$ 0 = 0

• For every non-zero number, say a, the inverse of the number exists given by 1/a such that the product of the number and its inverse results in the product being 1:

a $\cdot$ 1/a = 1

• Multiplication of a number with itself can be represented in the form of an exponential of the number. Formally, the multiplication of ‘a’ with itself for ‘n’ times is represented in the form of exponential as aⁿ. 
• An extension of the above property results in the addition of exponents when numbers with the same bases are multiplied. This can be expressed as:

(aⁿ) x (a^m) = a^{(n + m)}

Method of Computation

The most common method of multiplication is called the “long multiplication” method which builds on the multiplication tables of single-digit numbers and can be used to multiply two numbers of any digit length. For simplicity, the method is illustrated for 2 numbers ab and cd – each 2 digit. 

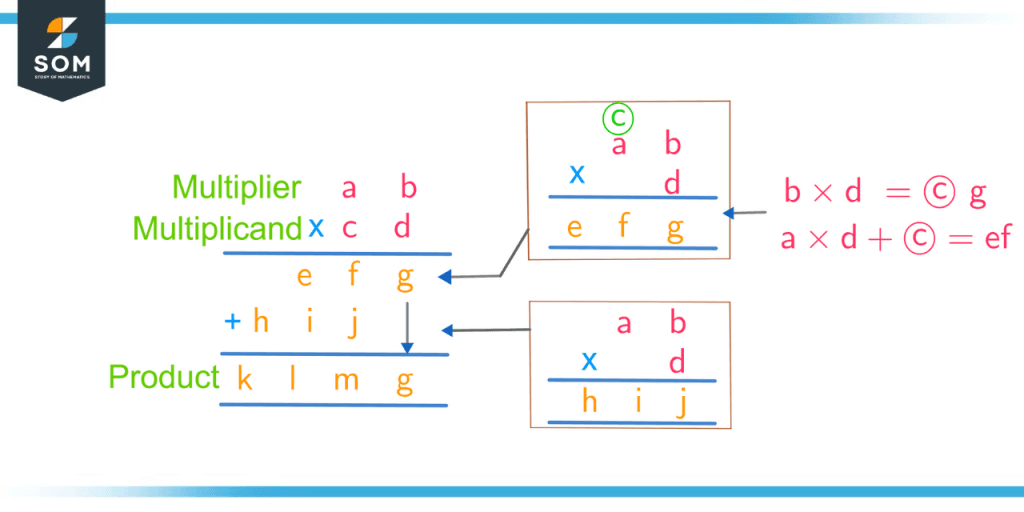
Figure 2: Multiplication of 2-digit numbers by the process of long multiplication.

In the first step, the multiplier ab is multiplied by the units place digit of multiplicand d. This can be further broken into the multiplication of units digit of multiplier b with d producing g and a carry c. Then a is multiplied with d and the carry is added from previous step to produce ef. 

Using the same procedure, the multiplier is then multiplied with the digit in tens place of the multiplicand and the result is shifted one place to the left. In the end, the byproducts are added to produce the final product. 

Special Multiplication Cases

• Multiplication of integers requires consideration of the sign of the multiplier and the multiplicand. Since each operand can either be positive or negative, this results in four cases which are shown in the figure below along with the sign of the product. 

Figure 3: Sign of product based on signs of multiplier and multiplicand.

• Multiplication of fractions is quite simple as the numerators of multiplier and multiplicand are multiplied with each other and denominators are multiplied with each other. This is given by:

(a / b) x (c / d) = ac / bd

• Multiplication of complex numbers with both a real and imaginary part uses the distributive property of addition and subtraction over multiplication along with basic complex algebra to simplify the result. This is expressed as:

(a + bi) (c + di) = ac + adi + bci + bdi²

• • Since i² = -1, hence:

(a + bi) (c + di) = ac + adi + bci + bd(-1)

(a + bi) (c + di) = ac + adi + bci – bd

• • This can be expressed in the general form of complex numbers as:

(a + bi) (c + di) = ac – bd + (ad + bc)i 

An Example of Multiplication

John goes to the store to buy some grocery items. Each item costs 38 dollars. Compute the cost of buying 12 items. 

Solution

The total cost will be the product of the cost of one item and the total number of items. 

Total cost = cost of one item x total items

Total cost = 38 x 12

The product can be evaluated by using the method of long multiplication as shown below.

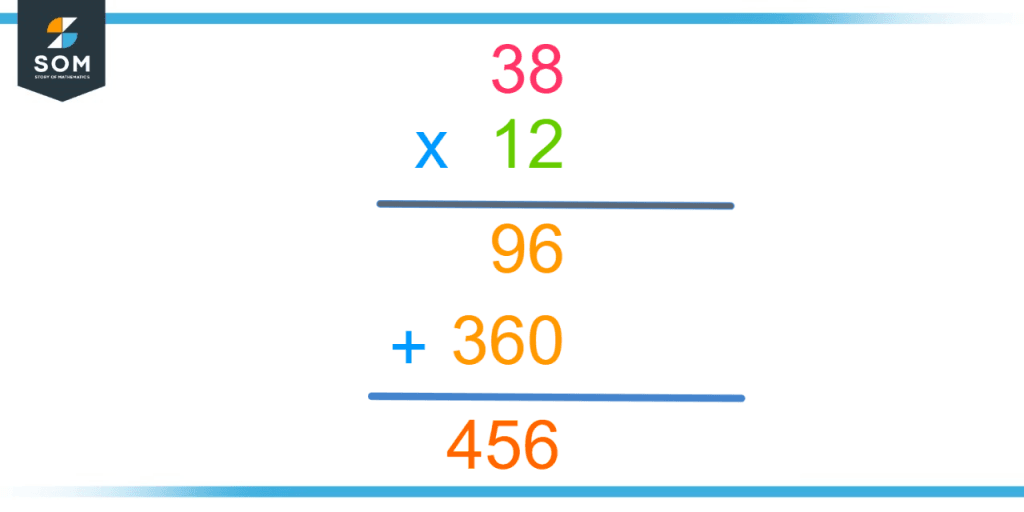
Figure 4: Multiplication of 38 and 12 through long multiplication.

Hence the total cost of the items will be 456 dollars. 

All images/mathematical drawings were created with GeoGebra.

Multiple Definition < Glossary Index > Multiplication Tables Definition