Multiplication Tables|Definition & Meaning

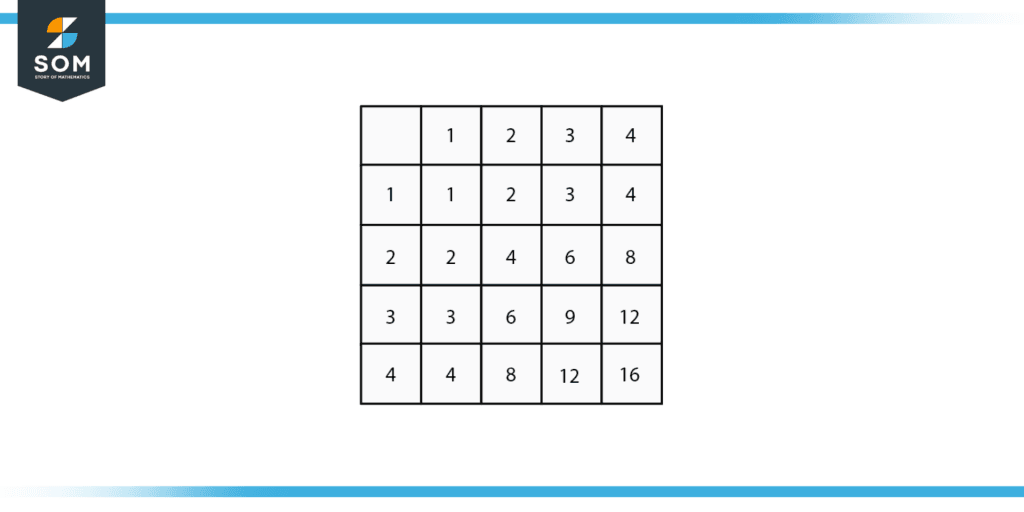
Figure 1: A multiplication table of 4. 

A table that displays the results of multiplying two integers is a multiplication chart. It is standard to write one set of numbers in the left column and the other set in the top row. An array of integers in a rectangle shape is used to list the products. Repeated addition is known as multiplication.

What Is Multiplication?

The most effective technique to explain multiplication is to use “groups of” rather than “times.” Multiplication is the process of adding sets of numbers together. Now suppose you have divided your students into 4 groups, and each group has 2 students. The total number of students would be:

Since there are s 4 groups of 2. So 2 times 4 make:

2 x 4 = 8

or

4 + 4 = 8

It is simpler to multiply groups of integers than to add them all together.

How To Use a Multiplication Table?

First, take a glance at the rows and columns in the following illustration that are shaded in grey.

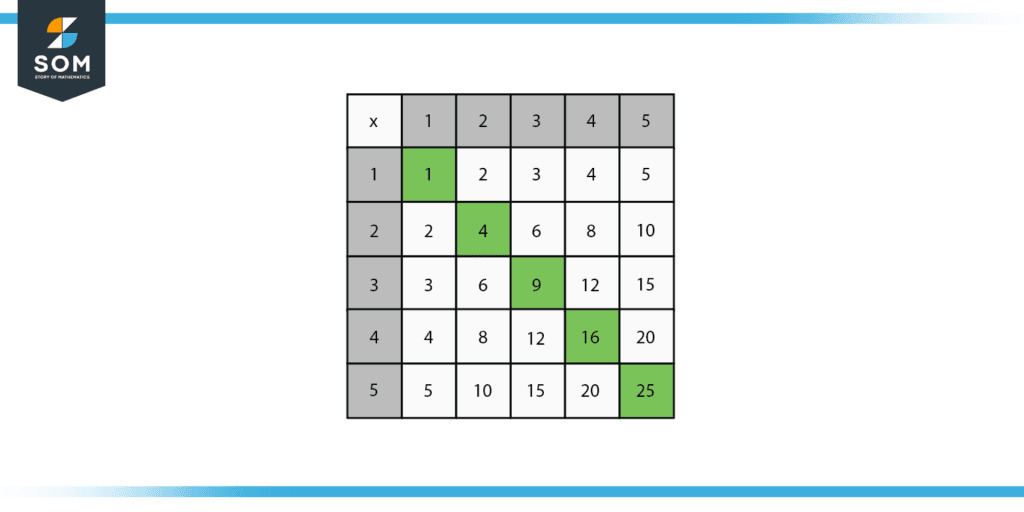
Figure 2: A multiplication table of 5.

Although columns are viewed vertically from top to bottom, rows are interpreted horizontally from left to right. On the diagram, the squares of the numbers, such as 1 x 1 = 1, 2 x 2 = 4, 3 x 3 = 9, etc., are represented by the green diagonal.

To comprehend how to analyze the multiplication chart, use the green diagonal. The value on the green diagonal is the product of the values in the grey-aligned columns and rows. For instance, the result of 4 and 4 is 16. 15 is obtained by multiplying 3 by 5, 5 by 3, etc.

To utilize the multiplication chart, select the two numbers you wish to multiply from the grey row and column, and then calculate the point at where an imaginary horizontal and vertical line—drawn from the grey column and row, respectively—would cross to yield the product of the two values.

Analyzing a Multiplication Table

The following steps are required to analyze a multiplication table:

• The first step entails picking the top row’s second number and the first number from the leftmost column’s list of numbers.
• The second step involves moving the first number down a column and the second number along a row. The result is found in the cell in which the two numbers intersect.
• For instance, 5 is along the row while 6 is in the column. Hence, 5 × 6 = 30.

Understanding Multiplication Table

There are two sections to a multiplication chart: the lower times table and the higher times table.

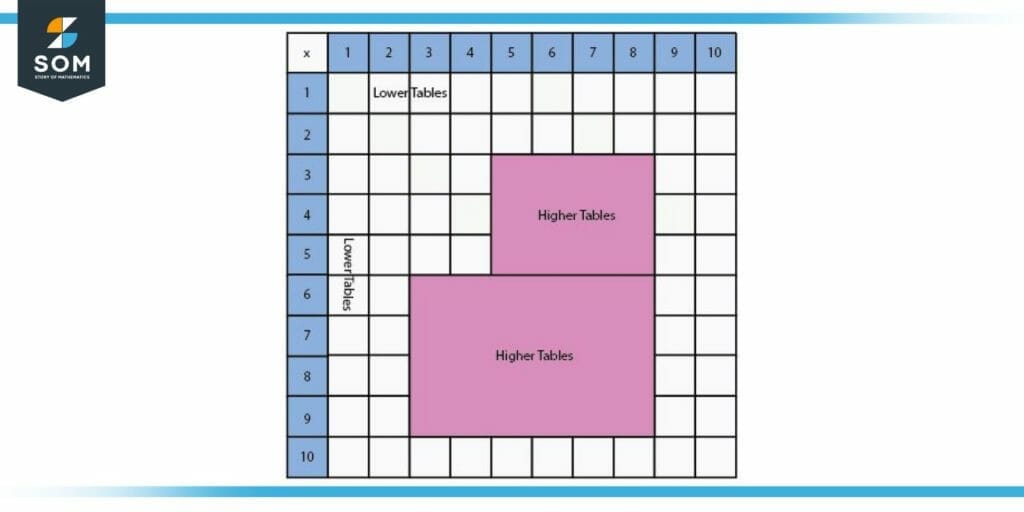
Figure 3: Sections of a multiplication table.

Because they have a pattern, the multiplication tables for 1, 2, 5, and 10 are simpler to memorize.

• The number itself is the product of any number and 1. For example, 3 multiplied by 1 will still be 3.
• Any integer is doubled when it is multiplied by 2. For instance, 4, when multiplied by 2 gets doubled, i.e., 8.
• In the multiplication table for five, the ones digit shift between 0 and 5. 
• The fact that zero is always the digit in the ones spot makes it simple to memorize the table of 10.

Lower time tables refer to those areas of the multiplication chart that are simple to remember. The upper time table refers to the remaining portion of the table.

The upper time table can also be memorized through exercise and repetitive addition.

The fact that the product is unaffected by the sequence in which any two numbers are multiplied is a crucial aspect of multiplication.

In a multiplication table, you may therefore obtain the same value for any product with the statement’s numbers reversed.

There are several blocks that are identical but in a transposed way.

Memorizing the Multiplication Table

When learning multiplication for the first time, memorizing 100 facts could seem like a lot of information to retain, but by making use of specific multiplication properties, the quantity of information that must be retained can be minimized.

Using Commutative Property To Memorize Multiplication Table

The order of multiplication is irrelevant, according to the commutative property of multiplication. Two numbers, a and b, are given. According to the commutative property of multiplication:

a x b = b x a

This is supported by the multiplication chart, which shows that the answer is always 15 whether we use the multiplication facts 3 x 5 = 15 or 5 x 3 = 15. For anything being multiplied, this is true. We only truly need to memorize the numbers below or above (and including) the diagonal line displayed in green on the chart because the sequence doesn’t matter. The number of multiplication facts we need to remember is practically reduced by half as a result of this property.

Using Identity Property To Memorize Multiplication Table

According to the identical property of multiplication, any number a multiplied by 1 equals a:

1 × a = a

Since 1 multiplied by any number equals that number, it is not required to remember the first row or column of the multiplication table as long as we are aware of this property.

Examples Using the Multiplication Table

Example 1

Check the multiplication table to see if the results of 7 x 3 and 3 x 7 are the same.

Solution

In order to determine 3 x 7, first find the row containing all multiples of 3. Next, locate the column that has multiples of 7. You can find out the value of the product of 3 and 7  is 21, which is in the cell where they overlap.

Find the row containing all the multiples of 7 before attempting to find 7 x 3. Next, look for the column that has multiples of 3. You can determine the product of 7 and 3 to get 21 by looking at the cell where they intersect.

Consequently, the results of 3 x 7 and 7 x 3 are the same.

Example 2

How do you use a multiplication table to find 4 multiplied by 2?

Solution

We must locate the row that displays the 4 time tables and the column which displays the table of 2 in order to determine 4 x 2. The next step is to locate the region where they cross. They cross over at 8.

Therefore, we can conclude by making use of the multiplication table that 4 x 2 = 8.

All images/mathematical drawings were created using GeoGebra.

Multiplicand Definition < Glossary Index > Multiplicative Identity Definition