Multiplier|Definition & Meaning

What Is a Multiplier?

A multiplier is a number or function used to scale or multiply a quantity in mathematics. Multiplication is also included as an arithmetic operation, along with addition, subtraction, and division. They are used in many branches of mathematics, from basic arithmetic to advanced abstract algebra and number theory.

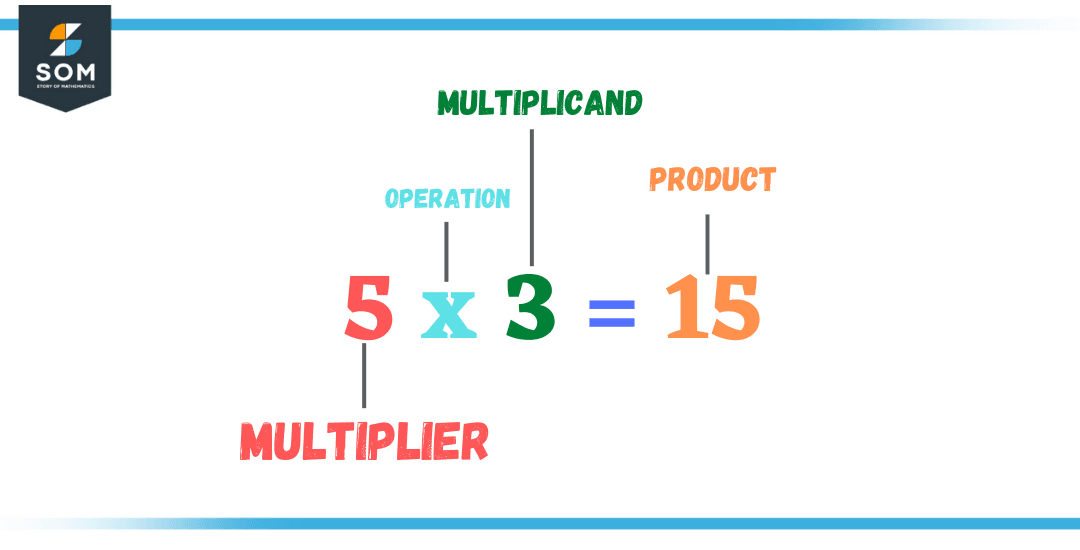
Figure 1 – Multiplier, multiplicand, and product

Notation

They are represented using various notations, including the symbol “x” or “*” exponents and factors. It plays an important role in many mathematical concepts. Multiplication can also be represented using the notation of exponents, such as 2³ = 8, where the base is 2, and the exponent is 3.

The Multiplier in Basic Arithmetic

When we multiply two numbers, one number is known as the multiplier, and the other is known as the multiplicand. For example, in the expression:

2 x 3 = 6

2 is the multiplier, and 3 is the multiplicand. The result of the multiplication, 6, is also known as the product.

Multipliers can also be represented using the notation of exponents. For instance, let’s say a and b are two arbitrary numbers; the product of a and b can be written as a$^1$.b$^1$, or simply as a . b. However, if we want to represent the product of a and itself b times, we can use the notation a$^b$, which is called “a raised to the power of b” and is equivalent to a multiplied by itself b times.

This notation can also be used to represent the product of more than two numbers, such as a².b³.c⁴, which is equivalent to (a.a).(b.b.b).(c.c.c.c).

In basic arithmetic, multipliers are also used to find the product of a number and 10, 100, 1000, etc. This process is called “scaling” and is used to represent numbers in different forms, such as decimals and scientific notation. For example, the number 5 can be scaled to 50 by multiplying it by 10 and to 500 by multiplying it by 100.

Multipliers can also be used to find the product of a number and a fraction. In this case, the number is multiplied by the numerator of the fraction, and the result is divided by the denominator. For example, to find the product of 5 and 1/2, we multiply 5 by 1 and divide by 2, resulting in 2.5.

The Multiplier in Basic Algebra

In basic algebra, a multiplier is a number or a variable that is used to scale or multiply a variable or an expression. Multipliers are used in algebraic equations and expressions to represent repeated addition or scaling of a variable or expression.

Figure 2 – A basic quadratic equation

One of the most common uses of multipliers in basic algebra is in linear equations. In a linear equation, the variable is multiplied by a constant coefficient, also known as a multiplier, to represent the slope of the line. For example, in the equation:

y = 2x + 3

The multiplier is 2, which represents the slope of the line. The variable x is the multiplicand, and the constant coefficient 3 is the y-intercept.

Another common use of multipliers in basic algebra is in solving equations. They are used to cancel out or eliminate a variable or term on one side of an equation. For example, in the equation:

2x + 3 = 5x – 1

We can multiply both sides of the equation by 2 in order to eliminate the x term on the left side. This results in:

4x + 6 = 10x – 2

which can then be simplified to 6 = 6x, and then x = 1.

In polynomials, multipliers are used to represent the degree of a term, which is the exponent of the variable. For example, in the polynomial 3x² + 2x -1, the multipliers are 3, 2, and -1, and the multiplicands are x², x, and 1. The degree is defined as the largest exponent in the whole polynomial; in this matter, 2.

Multipliers are also used in basic algebra for factoring polynomials, which is the process of finding the common factors of the terms of a polynomial. For example, in the polynomial 6x² + 9x – 3, we can factor out the common factor of 3x to get 3x(2x + 3) – 1. This process is useful in solving equations and simplifying expressions.

The Multiplier in Calculus

In calculus, multipliers are numbers or functions that are used to scale or multiply a quantity. They are used in various concepts, such as derivatives and integrals.

In derivatives, multipliers are used to find the product of a function and its derivative. For instance, in the product rule, the first function and its derivative are products that make up the derivative of the product of two functions, plus the product of the second function and its derivative.

For illustration, the product rule frames that if two functions f(x) and g(x) are given as a product with the whole derivative, then:

(f(x)g(x))’ = f'(x).g(x) + f(x).g'(x)

In this case, the multiplier is the derivative of the function, f'(x) and g'(x).

The Multiplier in Number Theory

In number theory, multipliers are used to find the product of integers. They are used in various concepts such as prime numbers, greatest common divisor and least common multiple, and modular arithmetic.

In the analysis of prime numbers, it is an integer that is more significant than 1 and is divisible by only 1 and itself. In this context, a prime number can be considered as a multiplier of itself and 1. For instance, the process of prime factorization of 12 is 2² * 3, where 2 and 3 are multipliers.

In greatest common divisor (GCD) and least common multiple (LCM), using multipliers can help us find a number that is the greatest common factor of two or more entities.

The GCD can be defined as the most significant number that divides each of the integers without a remainder, whereas the LCM is described as the least significant number that is a multiple of each of the integers. For illustration, the GCD of 12 and 8 is 4, and the LCM is 24.

In modular arithmetic, multipliers are used to find the product of a number within a certain modulus. For example, in the expression (5 x 3) mod 7, the product of 5 and 3 is 15, but since we are working in modulus 7, the result is 15 mod 7 = 1. In this context, 5 and 3 can be considered multipliers, and 7 is the modulus.

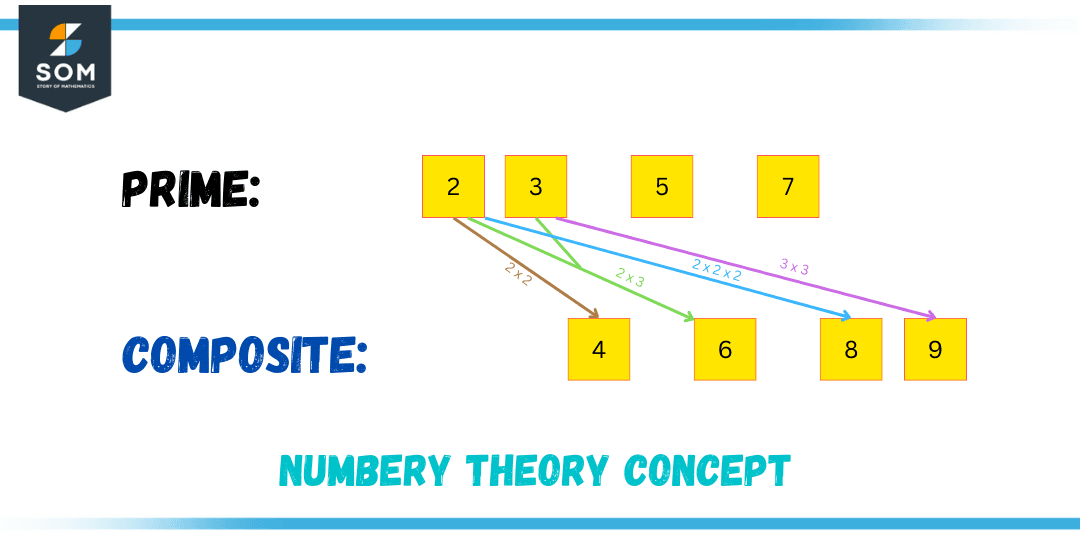
Figure 3 – A concept of Number theory

Solved Example of an Equation Involving Multipliers

Solve the equation:

3x² + 2x – 6 = 0

Solution

One way to solve this equation is by factoring the polynomial on the left side. To do this, we look for a common factor among the terms of the polynomial. In this case, we can factor out a -2 from the first two terms:

3x² + 2x – 6 = -2(x² + x/2 – 3)

Next, factor it using the difference of squares:

x² + x/2 – 3 = (x² – 9) + x/2 = (x + 3)(x – 3) + x/2

Now we can see that the equation becomes:

-2(x + 3)(x – 3) + x/2 = 0

Now, set each factor equal to zero and solve for x:

x + 3 = 0 x = -3

x – 3 = 0 x = 3

The solutions of the equation are x = -3 and x = 3. These are the values of x that make the equation true.

We can also combine the solutions in order to get the general solution of the equation:

x = -3, 3

So, in this example, we used multipliers -2 and 1/2 and factored out a common factor of -2 from the polynomial equation in order to solve for the roots. The solution of the equation is x = -3, 3.

All images are created using GeoGebra.

Multiplicative Identity Definition < Glossary Index > Multiply Definition