Multiply|Definition & Meaning

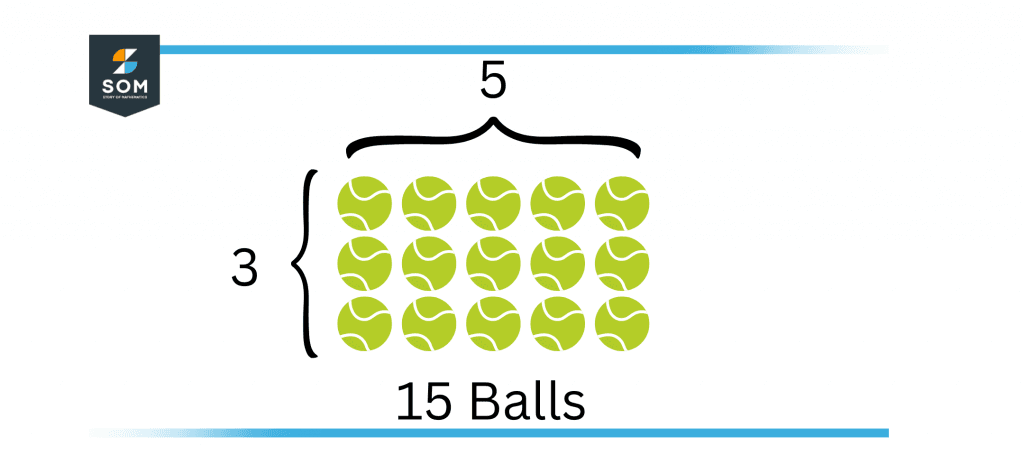
Figure 1 – Multiplying the number of rows with the number of columns gives the total number of balls

The process of multiplication has a minimum of three elements, which include two factors and a product. The product comes when the first factor is added into itself a certain number of times, in our case, the second factor. The number of factors goes on increasing as per the problem you come across.

What Is Multiplication?

To better understand, let’s take an example where we are to multiply the number of oranges contained in the two crates.

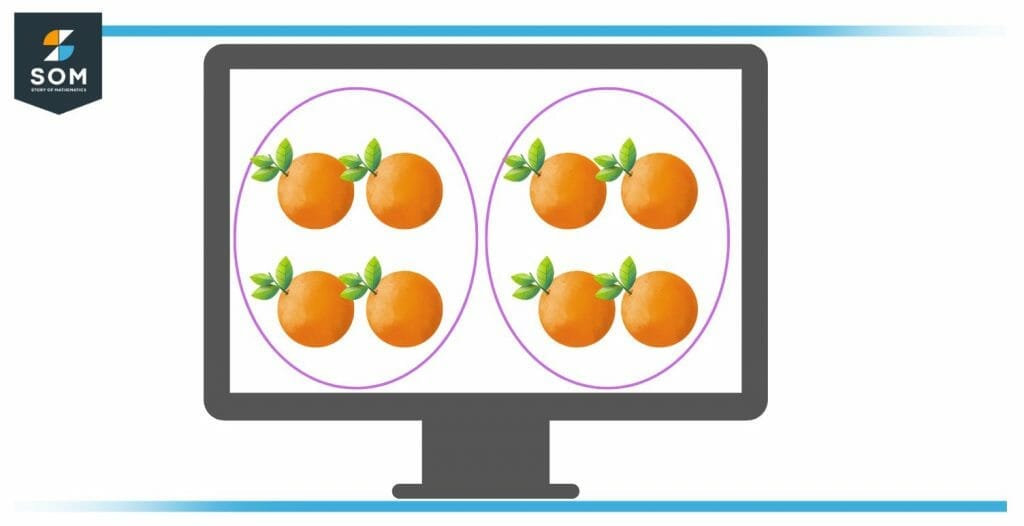
Figure 2 – Two baskets containing 4 oranges each

As per the figure, there are two crates each having 4 oranges in them, the crates are known as groups and thus there are two such groups.

If we make an addition here, the total number of oranges becomes:

4 + 4 = 8

However, since we have added the two groups of 4 oranges each, therefore we have multiplied four oranges by the value of two. So, we can also write is as:

2 x 4 = 6

This gives us a clear idea that addition and multiplication are very closely related to each other, and also 4 + 4 comes to be the same as 2 x 4. When we multiply any two numbers, the resulting number is called a product. The total number of elements in an individual group is known as a multiplicand, whereas the total number of the same groups is known as a multiplier. In our event, 4 stands to be the multiplicand, 2 comes to be the multiplier and 8 is the result of that multiplication known as the product.

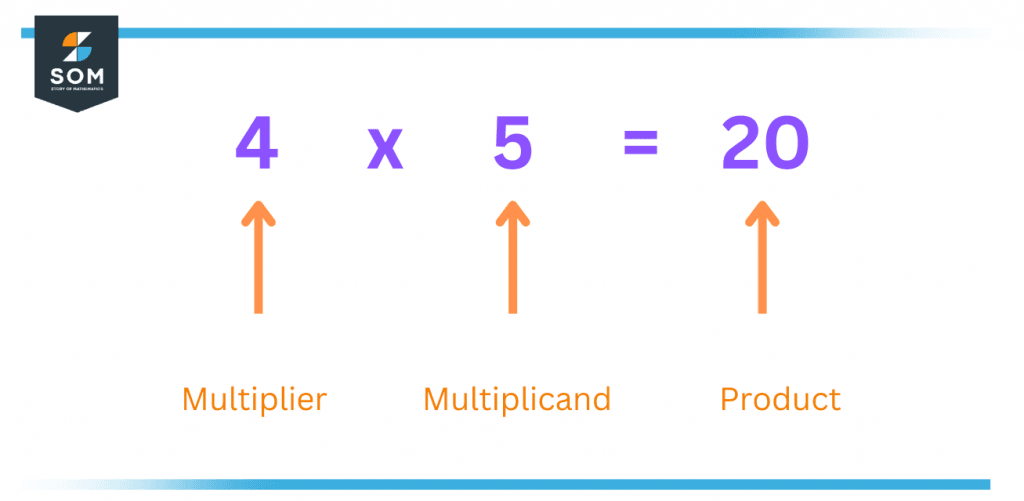
Figure 3 – Multiplier, Multiplicand, and the Product

There are several possible ways to deliver an equation that includes multiplication.

For instance, 2 x 4 = 8. It can be delivered as,

• Two multiplied by four is eight.
• Two times four is eight.
• Two fours are eight.

Symbols of Multiplication

Every piece of writing has its own way of representing multiple symbols. Some common symbols for multiplication are a cross (×), an asterisk (*), or a dot (·).

Usually, when we are writing in our notebooks, we most commonly use the cross sign as it is easier to draw and thus read. The other two symbols (asterisk and dot) are more commonly used in computer languages and higher mathematics, such as algebra and calculus.

A better visual of these symbols can be illustrated in the below figure.

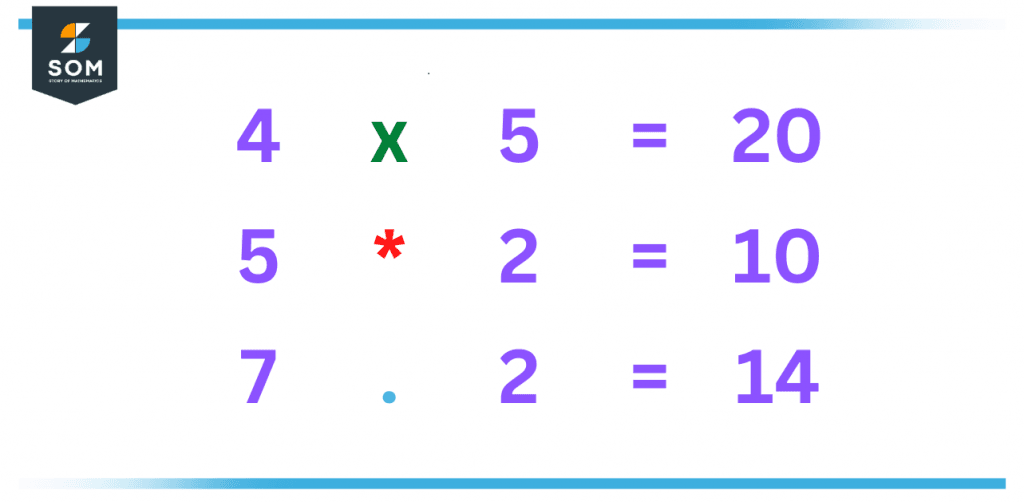
Figure 4 – Different symbols of multiplication

How To Multiply Integers?

Integers can be positive as well as negative, so when multiplying two integers, we need to be careful about the signs they are carrying. There can be three possible scenarios,

Multiplication of Two Positive Integers

When two positive Integers are multiplied, the product will always be a positive number.

For instance, 2 x 4 = 8.

Multiplication of One Positive Integer and One Negative Integer

When one positive and one negative integer are multiplied, the product will always be a negative number. Here the position of the negative sign has no effect on the overall result.

For instance, (–2) x 4 = (-8).

Multiplication of Two Negative Integers

When two negative Integers are multiplied, the product will be a positive number, as minus signs will cancel out each other.

For instance, (–2) x (-4) = 8.

How To Multiply Fractions and Decimals?

Fractions are a combination of two numbers sitting on top of each other. The upper one is known as the numerator, and below the numerator lies the denominator. To multiply a pair of fractions, we just simply multiply the numerators with numerators and denominators with denominators, such that

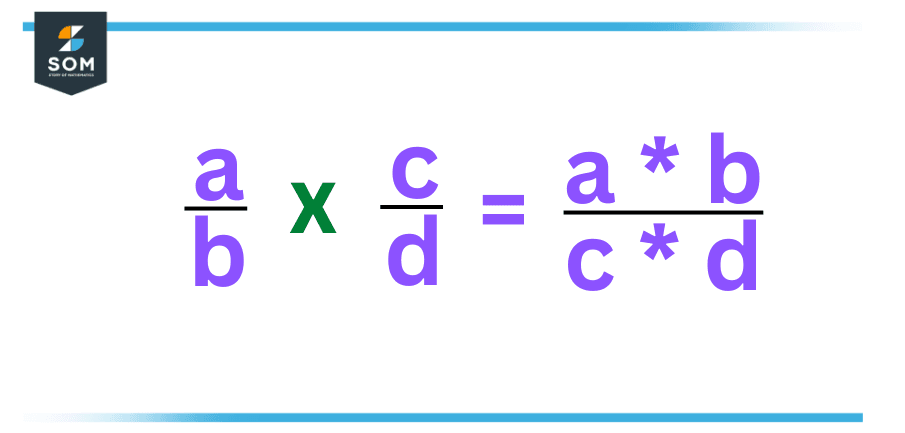
Figure 5 – Multiplying two fractions

Let’s say we have two fractions $\dfrac{1}{2}$ and $\dfrac{3}{4}$, then,

\[ \dfrac{1}{2} * \dfrac{3}{4} = \dfrac{1*3}{2*4} = \dfrac{3}{8} \]

Decimals can be multiplied in the same way as multiplying integers.

104 x 56 = 5824

Let’s say we have two decimals, 10.4 and 5.6. Multiplying these two decimals as whole numbers to see the result,

10.4 x 5.6 = 58.24

Now since the product is of two decimal point numbers, the product will have a decimal point add up to two places starting from the right, such that

Multiplying Numbers With Powers

In mathematics, powers represent the relation of a number to itself, defined by a base raised to an exponent. The exponent tells us how many times the number is being multiplied by itself concurrently, e.g., $2^2,\, (-5)^6$.

• If the bases are the same but the powers are different.
  • The powers add up, whereas the bases merge to become one common base. i.e. $x^m \times x^n = x^{m+n}$.
    For instance, $2^2 \times 2^4 = 2^{2+4} = 2^6 = 64$

• If the exponents are the same, but the bases are different.
  • The two different bases are multiplied, whereas the powers merge to become one common exponent. i.e. $x^m \times y^m = (xy)^m$.
    For instance,$2^2 \times 3^2 = 6^{2} = 36$

• If the bases and powers are different.
  • Since nothing is common here, each expression is first evaluated before being multiplied by each other. i.e. $x^m \times y^n = x^m y^n$.
    For instance,$2^2 \times 3^3 = (2)^2 (3)^3 = 4 \times 27 = 108$

Some Common Properties When Using Multiplication

Multiplication also follows the same pattern as an addition when it comes to having a set of properties, which are given as follows,

Commutative Property of Multiplication

The commutative property tells us that when two Integers are multiplied, the order of the factors will have no effect on the final product. Two multiplied by three is the same as multiplying three by two,

2 x 3 = 3 x 2

Associative Property of Multiplication

This Associative property says that if three or more numbers are multiplied one after, then their position will have no effect on the result, even if they are shuffled back and forth.

2 x (3 x 6) = 36

(2 x 3) x 6 = 36

Distributive Property of Multiplication

The Distributive property says that if there lies a sum of two numbers and we are to multiply another number with them, then the product will be the same as if we were to multiply those two numbers separately. For instance, if the sum of numbers is (2 + 4) and we multiply this sum by 6, we get:

6 x (2 + 4) = 36

• We can add 2 and 4 to get 6. Therefore, 6 multiplied by 6 gives 36.
• If we multiply 6, individually with each number, 6 x 2 = 12 + 6 x 4 = 24,
• We get the sum equal to 36. Hence, the distributive property is proven to be true.

An amazing thing about multiplication is that if you multiply any number in the universe by 1, you will get the exact number as the product. Also, if you multiply any number in the universe by 0, the end result will always be a 0, no matter how large the number might be.

Multiplication is a fun tool to learn despite being an arithmetic headache sometimes.

Solved Example

Find the solution of the following equation, also figure out which property is being used.

y = (3 x 6)(2+4)

Solution

First, compute the sum inside the braces (2+4) = 6.

Next, multiply the next closest digit to the sum, which is 6:

y = 3 x 3 x 6

y = 3 x 36

Now finally, multiply the remaining two digits to get the final product:

y = 108

The property used here is the distributive property of multiplication.

All images/mathematical drawings were created with GeoGebra.

Multiplier Definition < Glossary Index > Nano Definition