Natural Logarithm|Definition & Meaning

Figure 1 shows the demonstration of the natural logarithm of x. 

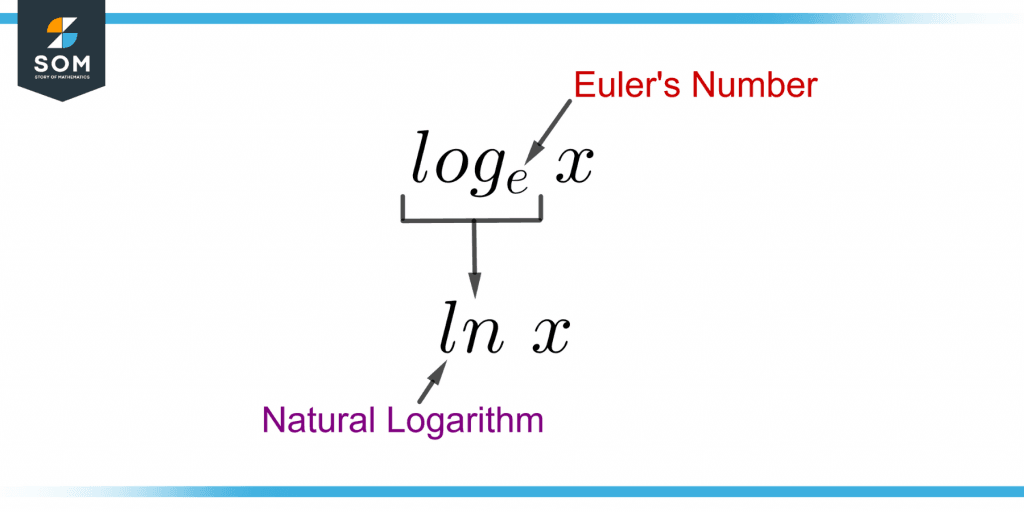
Figure 1 – Demonstration of Natural Logarithm and the Base “e” (Euler’s Number)

The natural logarithm of a number x defines how many times “e” is used in multiplication to get the given number x. It is the power of e to which it would be raised to become equal to the number x.

For example, the natural logarithm of 8.5 is 2.14006. This means that the number e is multiplied 2.14006 times to get 8.5. So, both can be written as:

ln(8.5) = 2.14006

e$^{2.14006}$ = 8.5

Logarithms can have any positive base other than 1, which will be its constant multiplier. In natural logarithms, the constant multiplier is e, as its base is e.

Concept of the Number “e”

To understand the natural logarithm, one must understand its base “e.” It is an irrational number as it is non-recurring and non-terminating. It can be written to a million decimal places, and so on, but it won’t have a repetitive pattern.

It was used by a scientist named Leonhard Euler, who derived its concept based on the different exponential growths happening in the universe.

Jacob Bernoulli discovered the constant e and formed the following equation:

\[ \lim_{ n \to \infty } { \Big( 1 + \frac{1}{n} \Big) }^{n} = e \]

The concept of “e” also comes from compound interest, as it also refers to the exponential growth of money.

Graphical Analysis of the Exponential function

An exponential function has the variable x as the exponent.  Mathematically, it is:

f(x) = b$^x$

Where b is a positive number except 1.

The most common exponential function is the function with the base “e.”

Figure 2 shows the graph for the exponential function:

f(x) = e$^x$

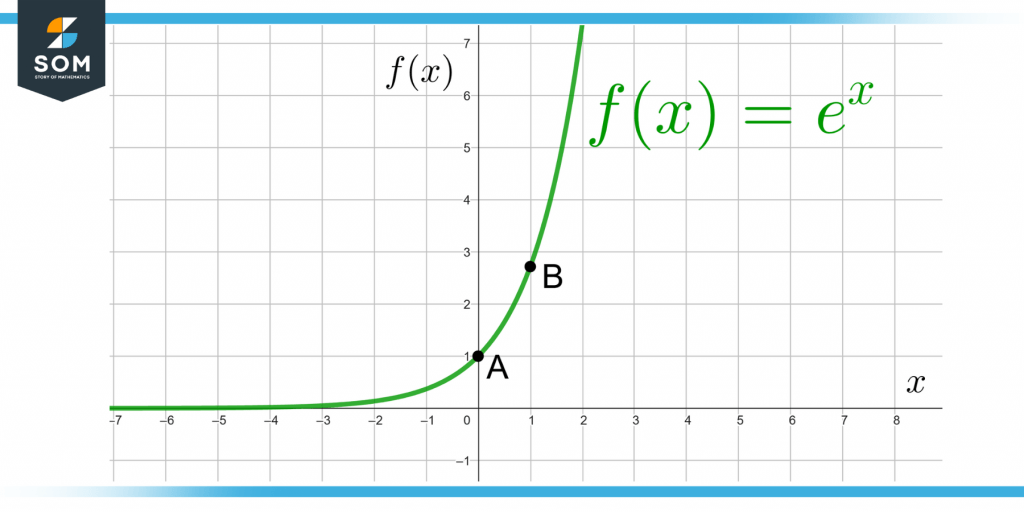
Figure 2 – Graph of an Exponential Function

The graph starts from negative infinity and goes to positive infinity. Point A represents the coordinates (0, 1), and point B as (1, e).

This exponential function is a very special function in mathematics because of its following properties.

Slope

The graph of the exponential function y = e$^x$ is a curve. It has a different slope at each point on the curve. If a tangent is drawn at a point, then its slope will be the slope of the curve at that point.

If a tangent line is drawn at point B, then its slope comes out to be e which is the same as the value of the function f(x) at that point. Also, at point A, the slope is 1 same as the function’s value.

Turns out that the slope at each point on the curve is equal to the value of the function at that point. This unique behavior makes it a special function.

Hence, it can be stated that the slope of the exponential function y = e$^x$ at a point on the curve is equal to the value of the curve at that point.

Area

Another unique trait is the area under the curve of the exponential function. Let L be any point on the curve. The area under the curve from negative infinity to the point L on the curve equals the value of the function at L.

No such function has this behavior in terms of its area and slope. That is why it is considered a unique function.

Graphical Analysis of the Natural Logarithmic Function

Figure 3 shows the graph for the function:

f(x) = ln(x)

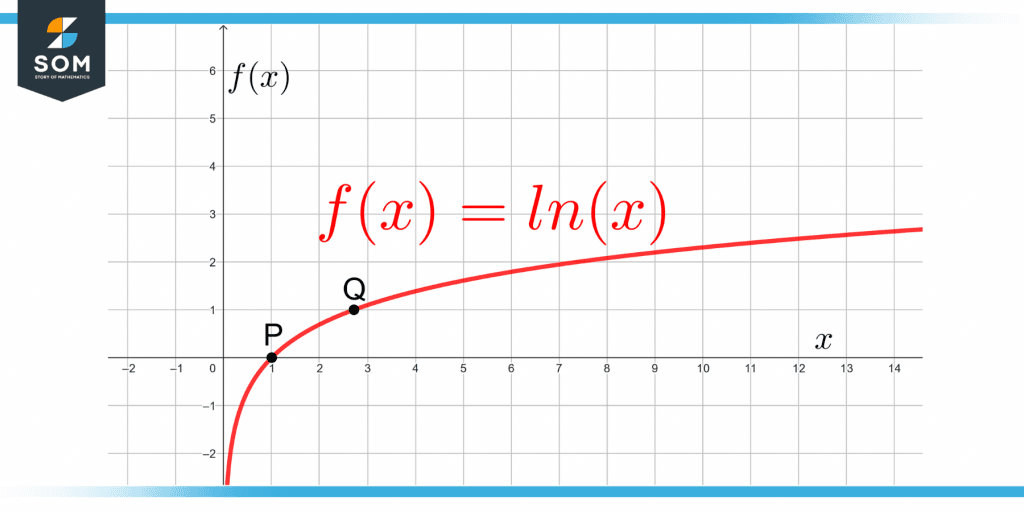
Figure 3 – Graph of the Natural Logarithmic Function ln(x)

Point P has the coordinates (1,0) and point Q has the coordinates (e,1). The unique properties of an exponential function make the logarithmic function also special. The base number “e” is common in both functions.

Relationship between Exponential and the Natural Logarithmic Function

The function ln(x) is the inverse of the function e$^x$, provided that the function ln(x) is a real-valued function of a positive variable. From this concept, the following identities are formed:

e$^{\ln (x)}$ = x

ln(e$^{x}$) = x

Figure 4 shows the exponential and the natural logarithmic function.

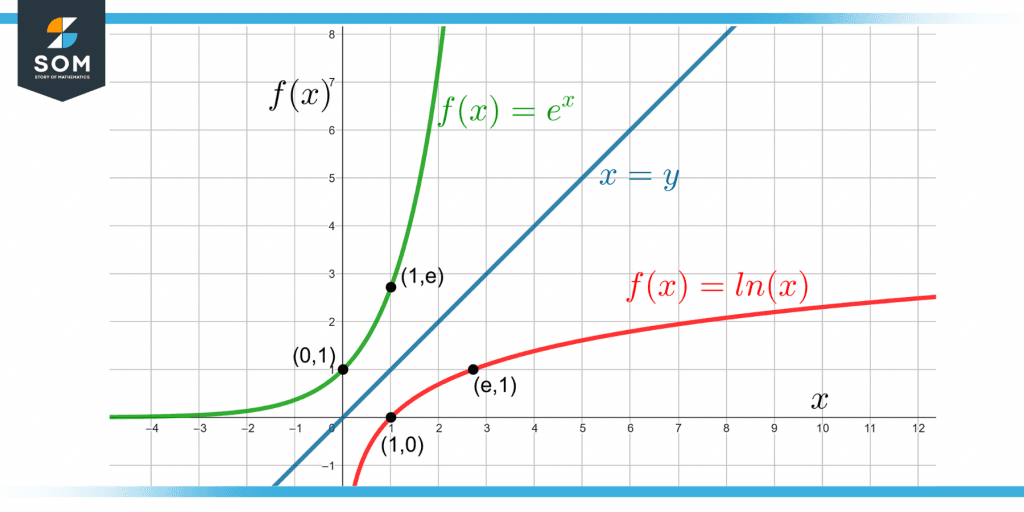
Figure 4 – Plot of the Natural Logarithmic Function and the Exponential Function as Inverses of Each Other

The function ln(x) is graphed by flipping the e$^x$ function over the line x = y.

Natural logarithms are used to solve equations in which the unknown variable is equal to an exponent of some other value. The problems of the decay constant and half-life are solved by using natural logarithms as they evolve exponentially.

Logarithms are used in solving problems related to compound interest.

Properties of Natural Logarithm

The following are the important properties of the natural logarithm:

ln(e) = 1

This is because e$^1$ = e.

ln(1) = 0

This is because e$^0$ = 1.

The multiplication of positive numbers x and y maps into addition in natural logarithms as:

ln(xy) = ln(x) + ln(y)

As for division:

ln(x/y) = ln(x) – ln(y)

The power y inside the ln function can be multiplied with the natural logarithm as:

ln (x$^{y}$) = y * ln(x)

Also, as x approaches the limit 0, the fraction ln(1 + x) / x becomes 1 as:

\[ \lim_{ x \to 0 } {\frac{\ln(1 + x)}{x} } = 1 \]

Differentiation of Natural Logarithmic Function

The differential of the function ln(x) is given as follows:

\[ \frac{d}{dx} \ln(x) = \frac{1}{x} \]

The differentiation of the function ln(ax), where a is a constant, is:

\[ \frac{d}{dx} \ln(ax) = \frac{d}{dx} [\ln(a) + \ln(x)] = \frac{d}{dx} \ln(a) + \frac{d}{dx} \ln(x)= \frac{1}{x} \]

Hence, the constant does not change the differential.

Integration of Natural Logarithmic Function

The integral of the function ln(x) is as follows:

\[ \int \ln(x) \ dx = x\ln(x) \ – \ x + c \]

Where c is a constant of integration.

Examples

Example 1

Solve e$^{7\ln(y)}$.

Solution

As:

7 * ln(y) = ln(y$^7$)

So:

e$^{7\ln(y)}$ = e$^{\ln(y^7)}$

The e and ln cancel to give the answer as:

e$^{7\ln(y)}$ = y$^7$

Example 2

Solve the equation:

2 * ln(x) – 3 * ln(1/x) = 10

Solution

As:

1 / x = x$^{-1}$

So:

2 * ln(x) – 3 * ln(x$^{-1}$) = 10

2 * ln(x) – 3(-1)ln(x) = 10

2 * ln(x) + 3 * ln(x) = 10

5 * ln(x) = 10

Dividing 5 on both sides gives:

ln(x) = 2

So, the final exact value is:

x = e$^2$

All the images are created using GeoGebra.

Nano Definition < Glossary Index > Natural Number Definition