JUMP TO TOPIC
Natural Number|Definition & Meaning
Definition
An integer greater than 0 is called a natural number. Natural numbers start at 1 and go up to infinity, like 1, 2, 3, 4, 5, etc.
A natural number is a number that is common and obvious in nature. It is a whole, positive number. The definition of natural numbers is exclusive of zero because counting starts with 1. This is how they look like in set notation and on a number line 1, 2, 3, 4, . . ., $\infty$
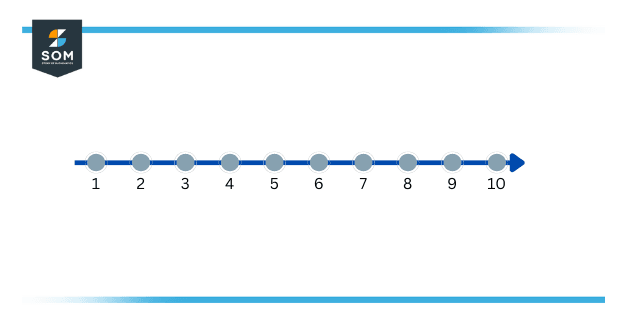
Figure 1 – Depiction of Natural Number
What Are Natural Numbers?
The numbers you use for counting are natural numbers, for example, its definition says that it includes all the positive numbers from 1 to infinity. These numbers are the fundamental bases of the number system and they occur in nature. Therefore, we see examples of natural numbers everywhere around us in the world.
Natural numbers are exclusive of fractions, decimals, zero, or negative values. They are tallies of occurrences, but they also order things on a number line. The smallest natural number is 1. The natural numbers set starts with 1 as its lowest or starting value, and 1 is also the smallest possible difference between any two given numbers. For example, the closest numbers to 5 are 4 and 6, one less and one more, respectively.
Natural numbers are countably infinite which means that you can count all the possible values, but they extend to infinity, just as the right arrow on the number line of natural numbers indicates.
Natural Number Examples
By definition, natural numbers are used in your daily lives whenever you start to count something. Natural numbers quantify and order the primary things in your life.
Natural numbers help you to count objects. For example, our office has two cafeterias. They also help you order things by putting them on the number line. For example, you can order a country’s population by the counts of the people living there.
The following are examples of natural numbers:
- The number of sandwiches you ate today.
- The number of steps you walked today.
- Comparing to see whether Drake or Bob walks more steps.
- The number of students in your class.
Comparison With Other Types of Numbers
Natural numbers are also sometimes called counting numbers and ordinal numbers. They are discrete numbers that perform in a contrast to continuous numbers. Discrete numbers are counted but continuous numbers are measured. Natural numbers are the basic foundation on which other number types build by extension.
Difference Between Natural Numbers and Whole Numbers
Natural numbers are generally defined as primary counting numbers. The natural numbers in set notation look like: {1, 2, 3, 4, 5, …..}. The letter that represents the Natural number is “N.” In natural numbers, the counting starts from the number 1. All natural numbers are whole numbers.
Whole numbers are defined as a set of natural numbers and an additional zero. The whole numbers in set notation look like: {0,1, 2, 3, 4, 5, ….}. The letter “W” represents the Whole numbers. With whole numbers, the Counting number begins from 0. It is said that all whole numbers are not natural numbers.
Whole numbers include all counting numbers or natural numbers and they add the zero, as shown in the Venn diagram. Whole numbers add zero. Zero is more of an advanced concept that mathematicians added to number theory relatively later.

Figure 2 – Venn Diagram
Difference Between Natural Numbers and Integers
Integers include all natural numbers, their negative values, and zero.
The sets below summarize and explain the various types of discrete numbers:
Natural Numbers = {1, 2, 3, 4, …, $\infty$}
Whole Numbers = {0, 1, 2, 3, 4, …, $\infty$}
Integers = {$- \infty$ , . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4, …, $\infty$}
Usage of Natural Numbers
Natural numbers are also known as “counting numbers” because they are in counting. For example, if you are counting something, you would use natural numbers (usually starting with 1). When writing down, natural numbers do not include decimal points (since they are integers), but the larger natural numbers might include commas, e.g. 20,000 and 127,567,100. Natural numbers can never include a minus symbol (-) because they are always positive.
In computer science, natural numbers are usually used in increasing values. For example, in a loop, the counter will usually be increased by one with each iteration of the loop. Once the counter reaches the limit (e.g., 5 in for (i=1; i<5; i++)), the loop ends and the code after the loop is executed.
Properties of Natural Numbers
Addition Property of Natural Numbers
The addition of two natural numbers results in a natural number only. Because Natural numbers are greater than 0 and the sum of anything greater than 0 will be greater than zero. For example:
30+43 = 73
When a natural number is added to a whole number the result will a natural number. For example:
0+30 = 30
Subtraction Property of Natural Numbers
When two Natural Numbers are Subtracted the result does not necessarily be a natural number. The reason is explained in the below examples.
11 – 6 = 5
In the above example the result is 5 which is a natural number, now look at the example below,
6 – 11 = -5
The result is -5 which is not a natural number so in this case, the subtraction of two natural numbers is not a natural number.
Multiplication Property of Natural Numbers
When a natural number is multiplied by the natural number the result will also be a natural number because when two numbers are multiplied and both are greater than 1 the result is also greater than 1. For example:
5 \times 4 = 20
Which is a natural number.
Division Property for Natural Numbers
Natural numbers do not hold the division property because division can produce numbers in decimals that are not natural numbers. For example:
12/3 = 4
A result is a natural number in this case but in the below case:
15/2 = 7.5
Which is not a natural number.
Solved Example of Identifying Natural Numbers
From the series of numbers given in the figure below, find natural numbers.

Figure 3 – A sequence of numbers; find the natural ones
Solution
Natural Numbers from the above-given list are 45, 7, and 80.
All images/mathematical drawings were created with GeoGebra.
