JUMP TO TOPIC
Negative|Definition & Meaning
Definition
A number is considered negative if its value is always below zero and it is preceded by the symbol for the negative sign (-) symbol.
What Are Negative Numbers?
A minus sign serves as a prefix for a number to indicate that it is a negative number. They may be written in integer, decimal, or even fractional forms. As an illustration, the digits –4, -15, -4/5, and -0.5 are examples of what are known as negative numbers.
What Are Negative Integers?
Numbers that have a value that is less than zero are considered to be negative integers. They do not contain any fractions or decimals in their totals. Negative integers include the numbers -7 and -10, for instance.
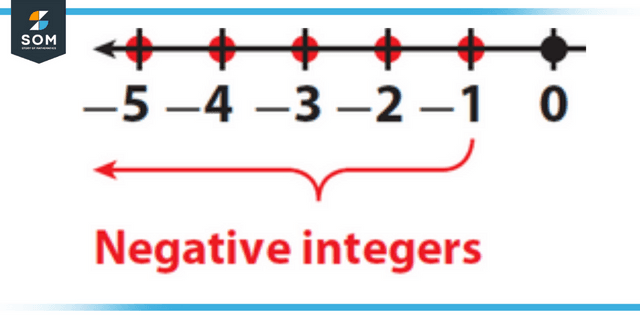
Figure 1: Representation of negative integers.
Formulas and Guidelines for Negative Numbers
When performing the four fundamental arithmetic computations of addition, subtraction, multiplication, and division on negative numbers, one must adhere to a predetermined set of guidelines.
- A negative number is obtained by adding two other negative numbers. For instance, -5 plus (-1) equals -6.
- The difference between two numbers can be calculated by adding positive and negative numbers. The sign of the absolute value with the greater magnitude comes before the outcome. For instance, -9 plus 3 equals -6.
- When a ‘-‘ number is multiplied by a positive one, you get another negative one. For instance, -9 multiplied by 2 equals -18.
- A positive number is produced when two negative numbers are multiplied For instance, -6 over -3 equals 18
- When splitting negative numbers, the result is positive if the signs of the numbers being divided are the same. For instance, -56 divided by -7 equals 8.
- If you divide negative integers and the results are still negative, check to be sure that the signs are the same. For instance, -32 divided by 4 equals -8.
Calculating Negative Numbers by Adding and Subtracting
We must commit the following rules to memory to successfully add and subtract negative numbers.
Addition of Numbers With a Negative Sign
Case 1
When adding a negative number to another negative number, we must add the two numbers together and include the negative sign in the solution. For instance, -7 plus (- 4) equals -7 minus 4, which equals -11. To put it another way, whenever you add two negative integers, you get another negative number.
Case 2
When adding a positive number to a negative number, we calculate the difference between the two numbers. Then we utilise the sign of the more excellent absolute value in the response. For instance, -9 plus (5) equals -4. The answer is -4 since the sign of the more excellent absolute value is being used in this calculation.
A number line is a helpful tool to grasp this concept better. The rule for using the number line states that when adding a positive number, one must travel to the right along the line.
Subtracting Negative Numbers
The process of subtracting negative numbers from positive numbers is similar to addition. Said, we need to keep in mind a rule that states:
The Subtraction Rule Is as Follows: Alter the sign of the second number that follows and the operation, which should be changed from subtraction to addition.
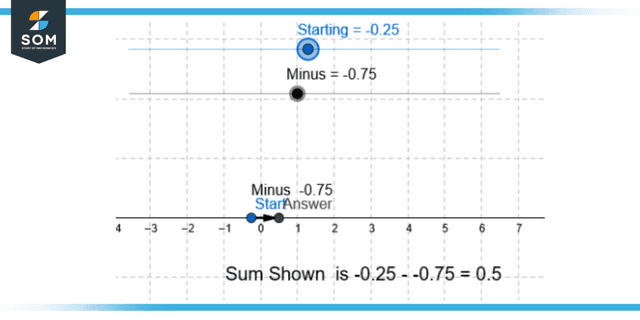
Figure 2: Representation of subtraction of two negative numbers.
Case 1
When we have to subtract a positive number from another positive integer, we use the formula for subtraction that was presented earlier in this paragraph. For instance, 5 – (+6) becomes 5 + (-6), 5 – 6, which equals -1.
Case 2
When we have to subtract a positive number from a negative number, we will stick to the same rule of subtraction that we used in the previous example, which states:
The Subtraction Rule Is As Follows: Alter the sign of the second number that follows and the operation, which should be changed from subtraction to addition. For instance, the expression -3 minus (+1) will yield -3 plus (-1). It can be concluded by saying that -3 minus -1 equals -4.
Case 3
The following rule of subtraction will guide us when we need to subtract a ‘-‘ number from another negative number:
The Subtraction Rule Is As Follows: Alter the sign of the second number that follows and the operation, which should be changed from subtraction to addition.
For instance, -9 minus (-12) multiplied by -9 plus 12 is 3. Because of this, 12 is now in the positive. We use the sign of the absolute value with the greater magnitude of 12, even if the answer is 3.
Performing Multiplications Using Positive and Negative Numbers
Rule 1 states that the outcome will be negative whenever the signs of the numbers being added together are different. (-) × (+) = (-) . (-). When we ‘x’ a negative number by a positive one, the result is always negative. In other words, the product is always a negative number. Consider the following: -3 times 6 is -18.
Rule 2 states that the result will be positive whenever the signs of the numbers are the same. (-) × (-) = (+); (+) × (+) = (+). To put it another way, regardless of whether the numbers being multiplied are positive or negative, the product of such a multiplication is always positive. For instance, -3 multiplied by -6 equals 18.
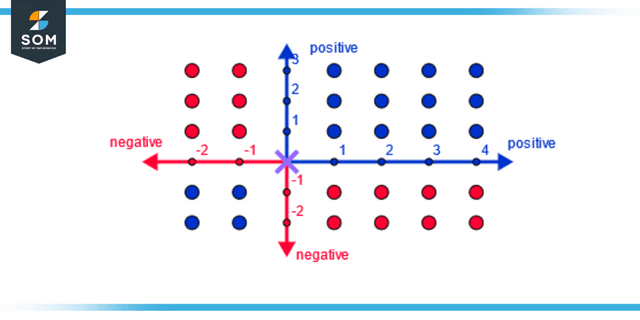
Figure 3: Multiplication of positive and negative numbers.
Calculating Differences Between Positive and Negative Numbers
Rule 1 states that the outcome of dividing a – number by a number is always going to be a negative number. (-) ÷ (+) = (-). For instance, (-36) divided by (4) equals (-9).
Rule 2 states that the answer to dividing a negative number by another negative number will always be positive. (-) ÷ (-) = (+). (-24) divided by (-4), for instance, equals 6.
Example 1
What is the sum of the following equation:
(-2) + (-3) + (-1) = ?
Solution
We know that when negative numbers are added, we get a negative number. So,
(-2) + (-3) + (-1) = -6
Example 2
What is the product of -5 and -6?
Solution
We know that the product of two negative numbers is a positive number. So,
-5 * -6 = 30
All images/graphs are created using GeoGebra.
