Number Line|Definition & Meaning

Our ability to perform basic arithmetic operations on numbers is greatly enhanced when we write them out on a number line. 

Overview 

Generally speaking, zero is taken as the origin or starting point of the number line. The origin divides the number line into two portions left portion and the right portion. The left portion represents the numbers that are less than zero. In other words, all the negative numbers. The right portion of the number line represents the numbers that are greater than zero, in other words, all the positive numbers.

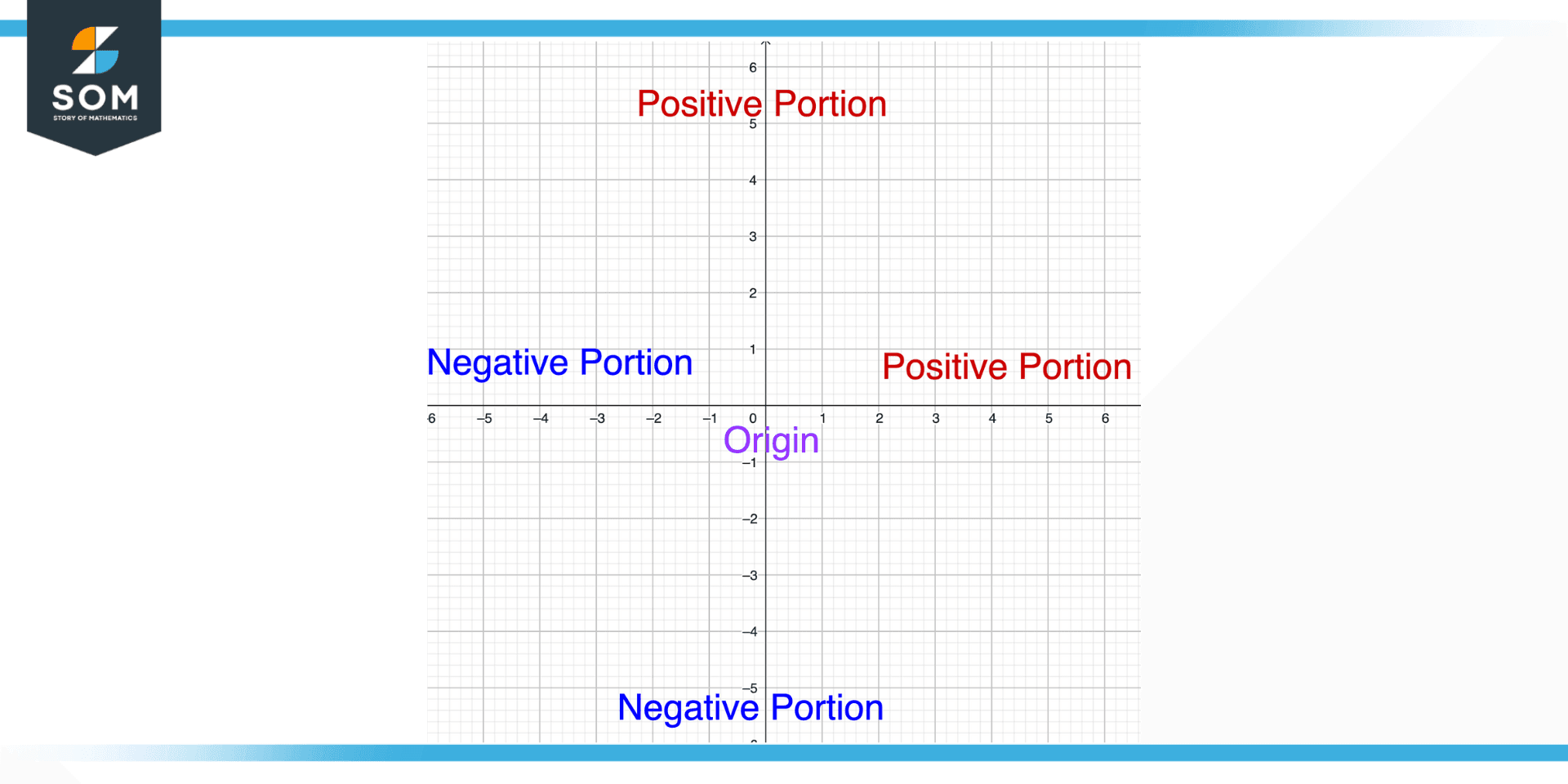
Figure 1 – Components of Number Line

The importance of a number line is to give a graphical representation and visualization of numbers that help in various applications related to probability, stochastic systems, and other statistical systems.

Components of Number line

We can divide the number line from Figure 1 into three parts: origin, negative area, and positive area. We will discuss them one by one.

Origin

The midpoint of the number line is known as the origin and it is denoted as “o.” Further, it divides the number line into two equal parts.

Positive Area

The right portion or right side of the origin is known as the positive area. All the numbers lying in this region are positive. The range of this portion is from natural numbers varying from greater than zero to positive infinity.

Negative Area

The left portion or left side of the origin is known as the Negative area. All the numbers lying in this region are negative. The range of this portion is from natural numbers varying from less than zero to negative infinity.

Procedure for Sketching Number Line

Step 1

Draw a line, either horizontal or vertical, according to the given specification. Often it’s our choice to draw a horizontal or vertical line that best suits the given visualization.

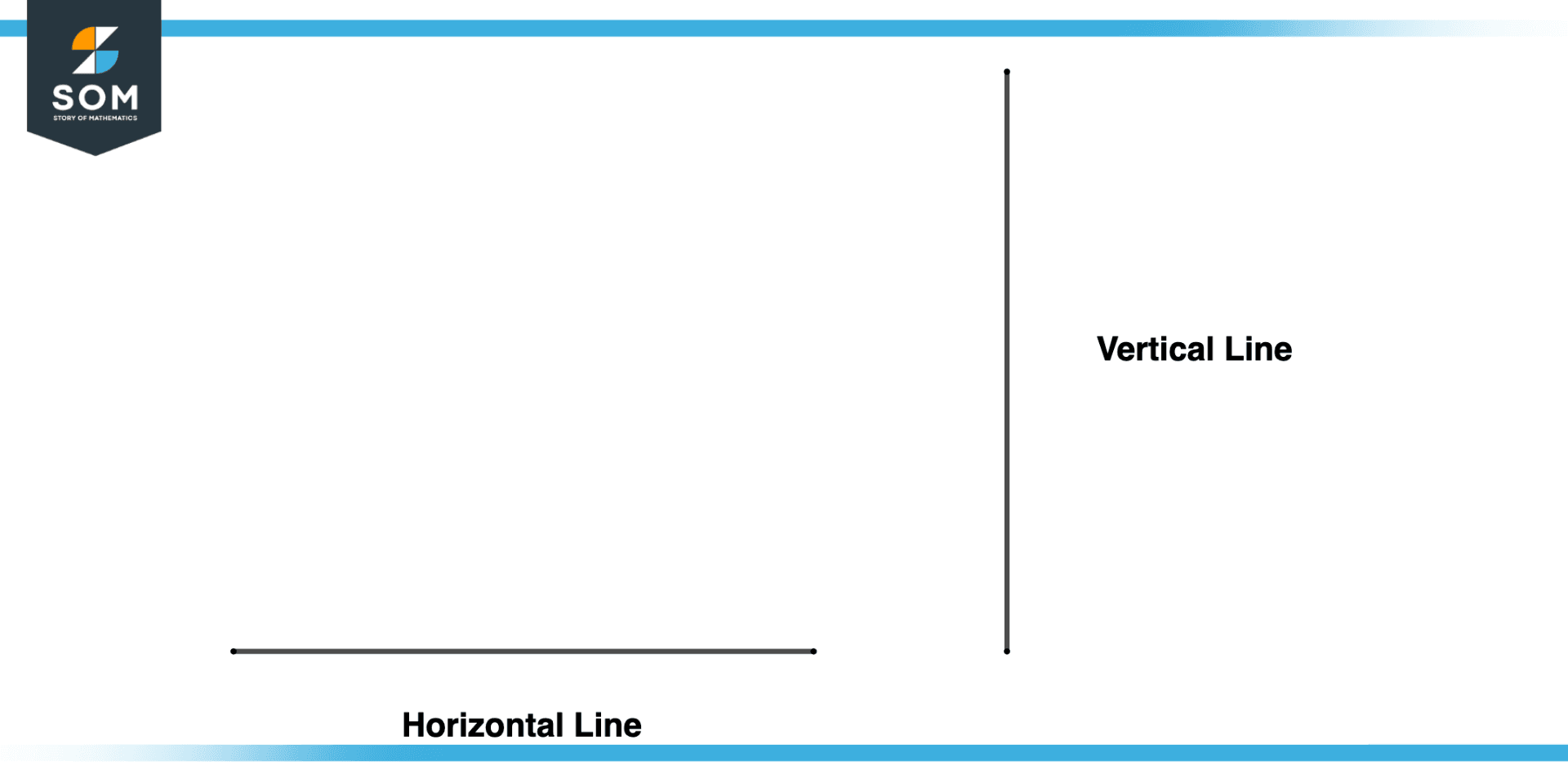
Figure 2 -Sketching Number Line First Step

Step 2

The second step is to select an appropriate scale according to the given problem. Suppose we want to plot 3; we can select a scale of 1. If we want to plot the number 10, we can select a scale of 2, and if we want to plot some greater number, then we will increase the scale factor accordingly. For example, to plot the number 30, we can take a scale of 5.

The reason for selecting scale is that while plotting numbers on the number line on a page or graph paper, there is limited space, so we have to choose the scale that can best plot in a given limited space.

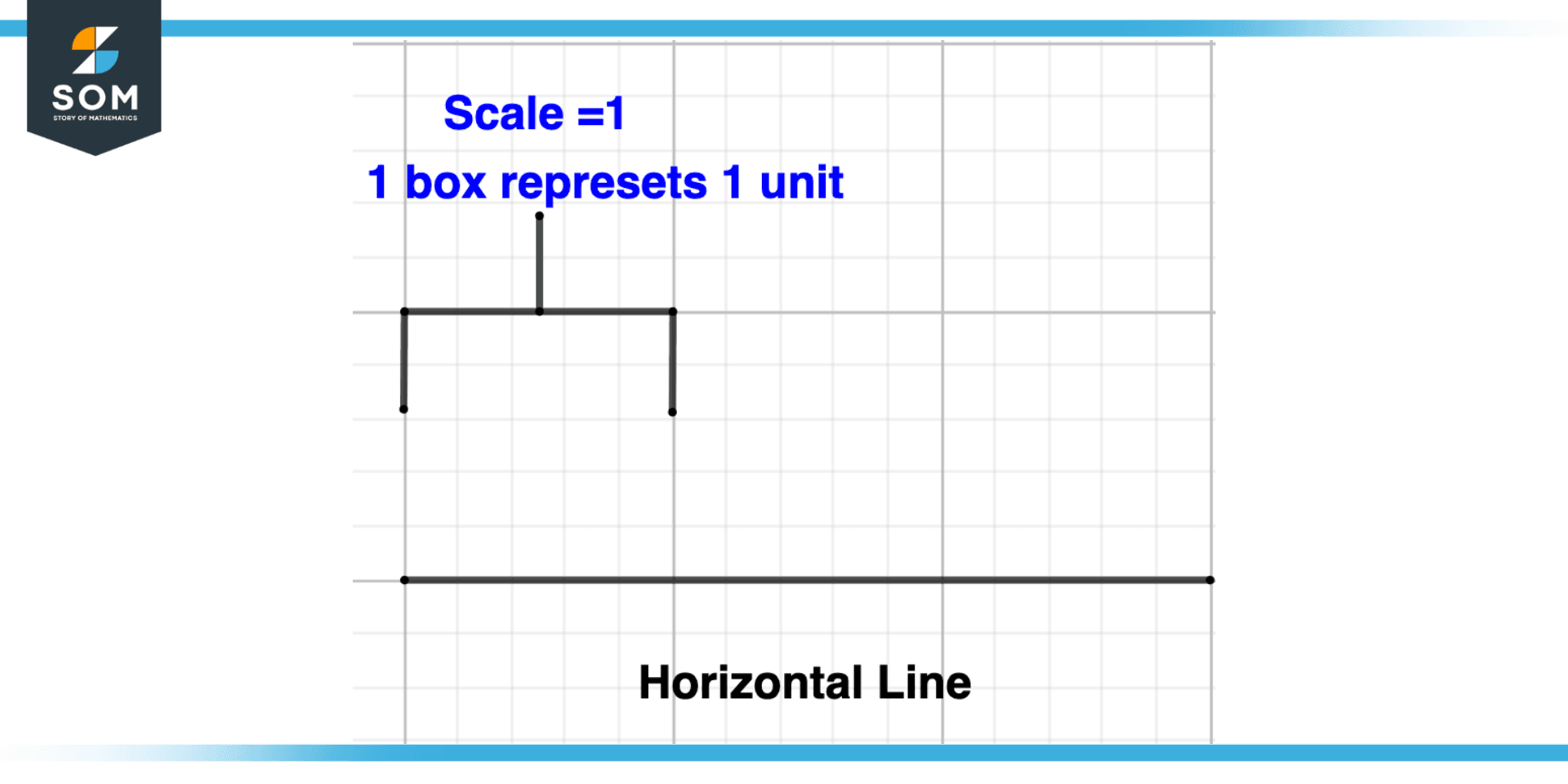
Figure 3 – Sketching Number Line Second Step

Step 3

The third step is to label the number line according to the selected scale. For instance, if we want to plot number 5 and we have chosen the scale as 1, then starting from origin 0, we will label the number line after every 1 unit space as we will mark the scale as 0, 1, 2, 3, 4, 5.

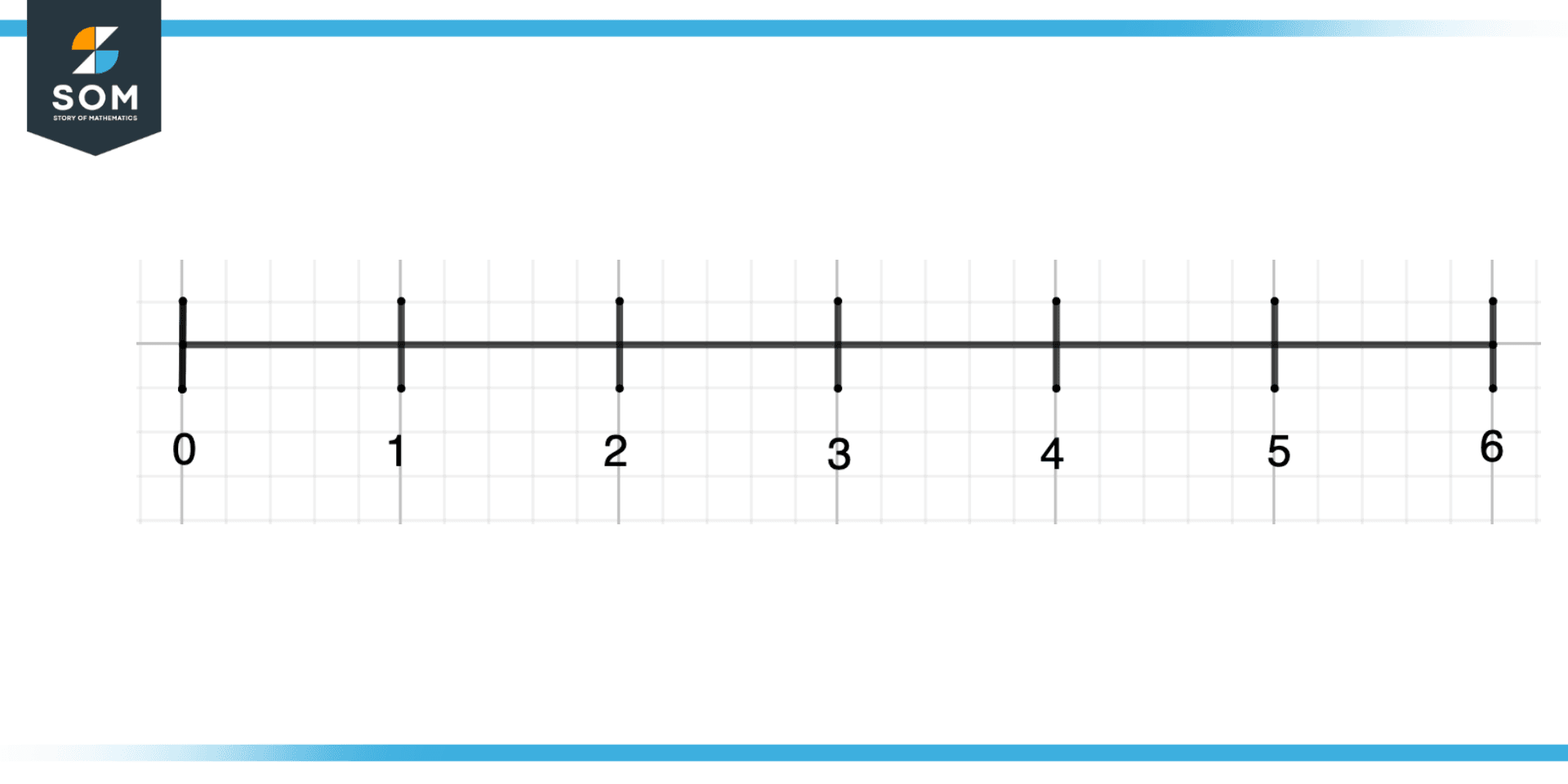
Figure 4 – Sketching Number Line Third Step

Step 4

After sketching the number line, the last step is to plot the number. For plotting the number, find the position of that number on a number line and highlight using either a dot or a cross.

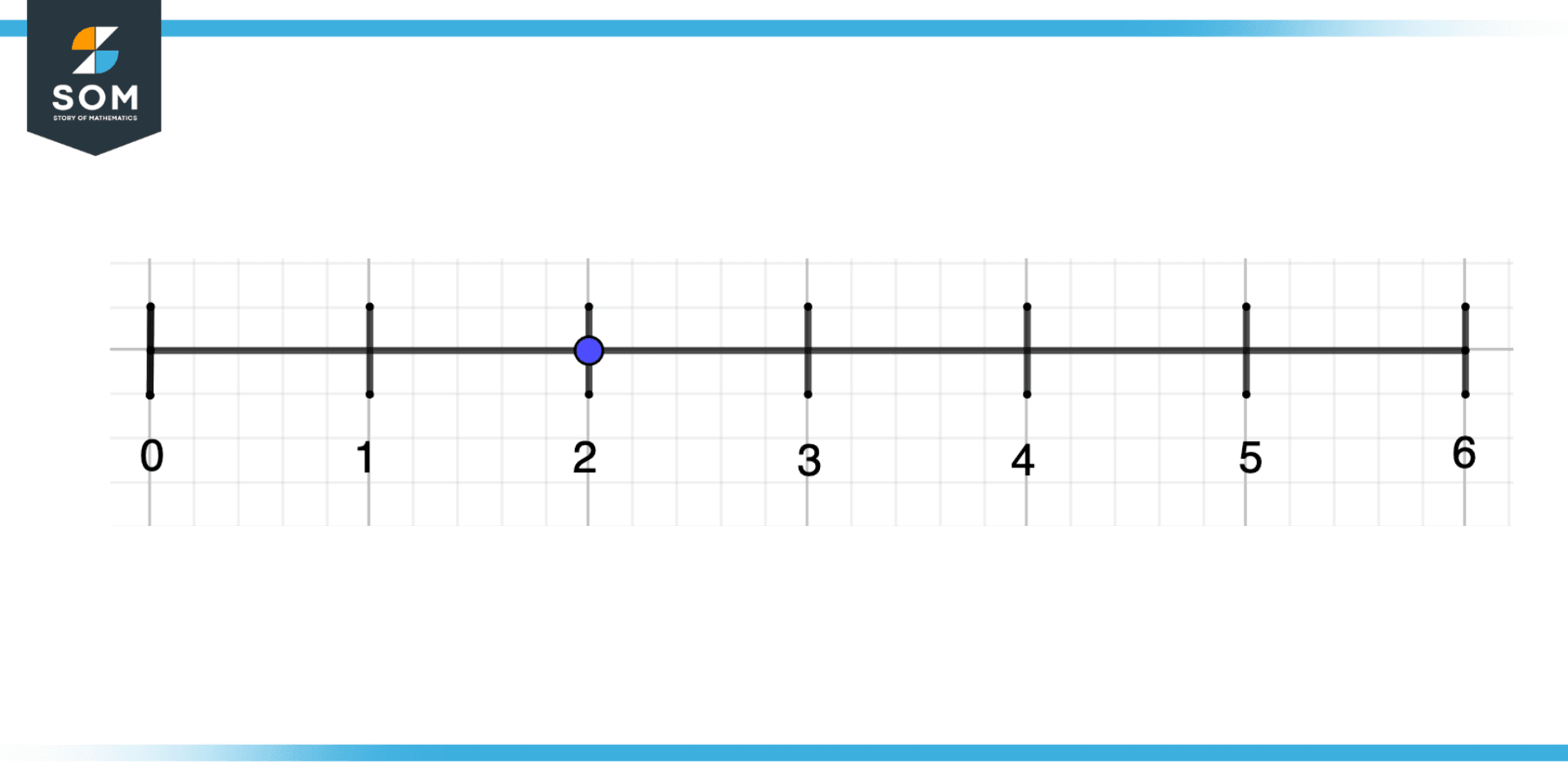
Figure 5 – Sketching Number Line Fourth Step

Addition of Positive Numbers on the Number Line

Suppose there are two numbers, 5 and 3, and we want to add them. First, we will sketch a number line with a scale of 1. Then, from the location of number 3 on the number line, we will move 5 steps towards the right side. The point where we stop will be the result of the addition of these two numbers. This is shown in the illustration shown below.

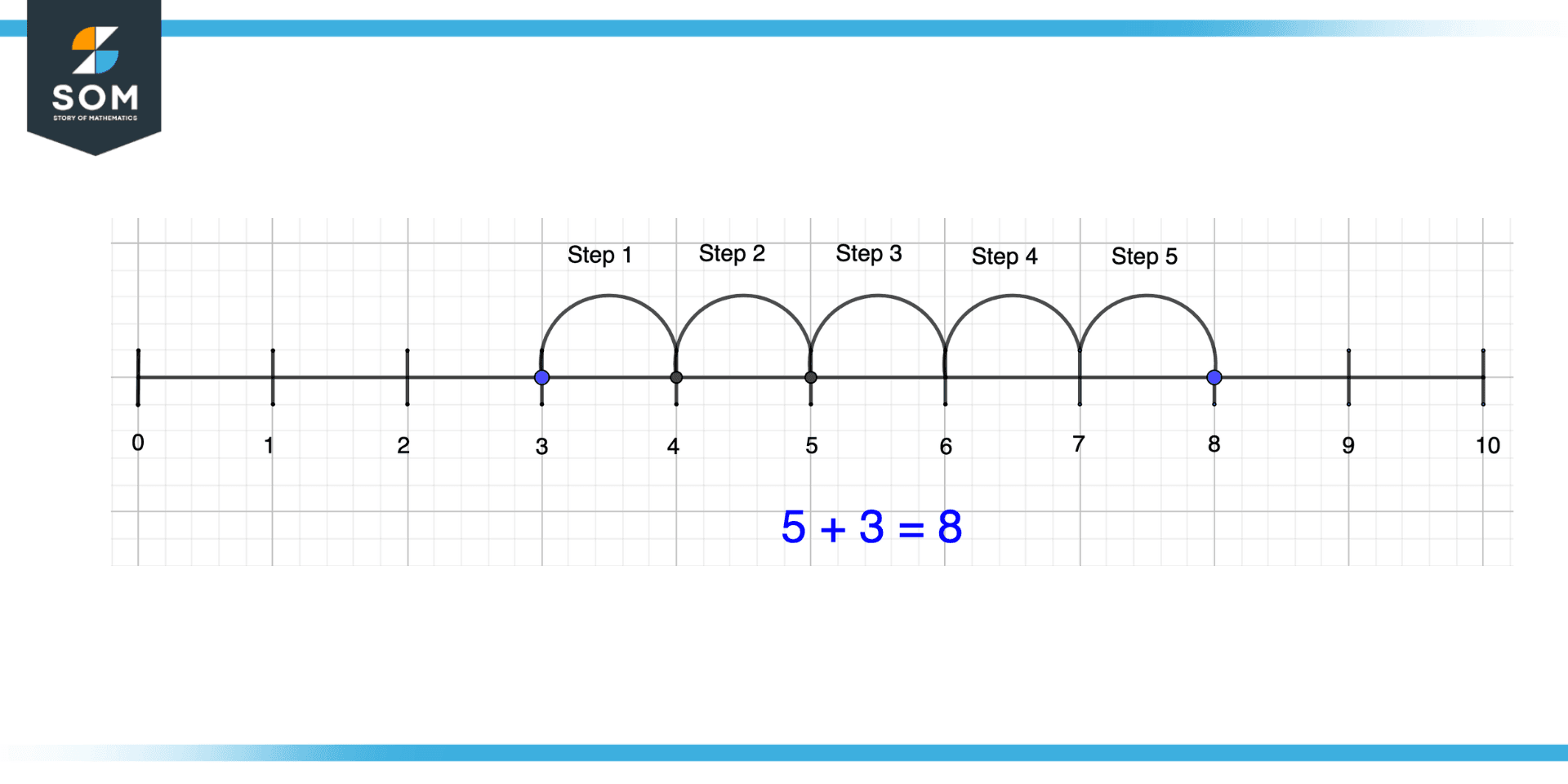
Figure 6 – Addition of Positive Numbers on Number Line

Subtraction of Positive Numbers on the Number Line

Consider two numbers 6 and 3 that we want to subtract. First of all sketch a number line with a scale of 1. Then, from the location of 6 on the number line, move 3 units backward. The position that we get after doing so will be the result of subtraction. This is shown in the illustration below.

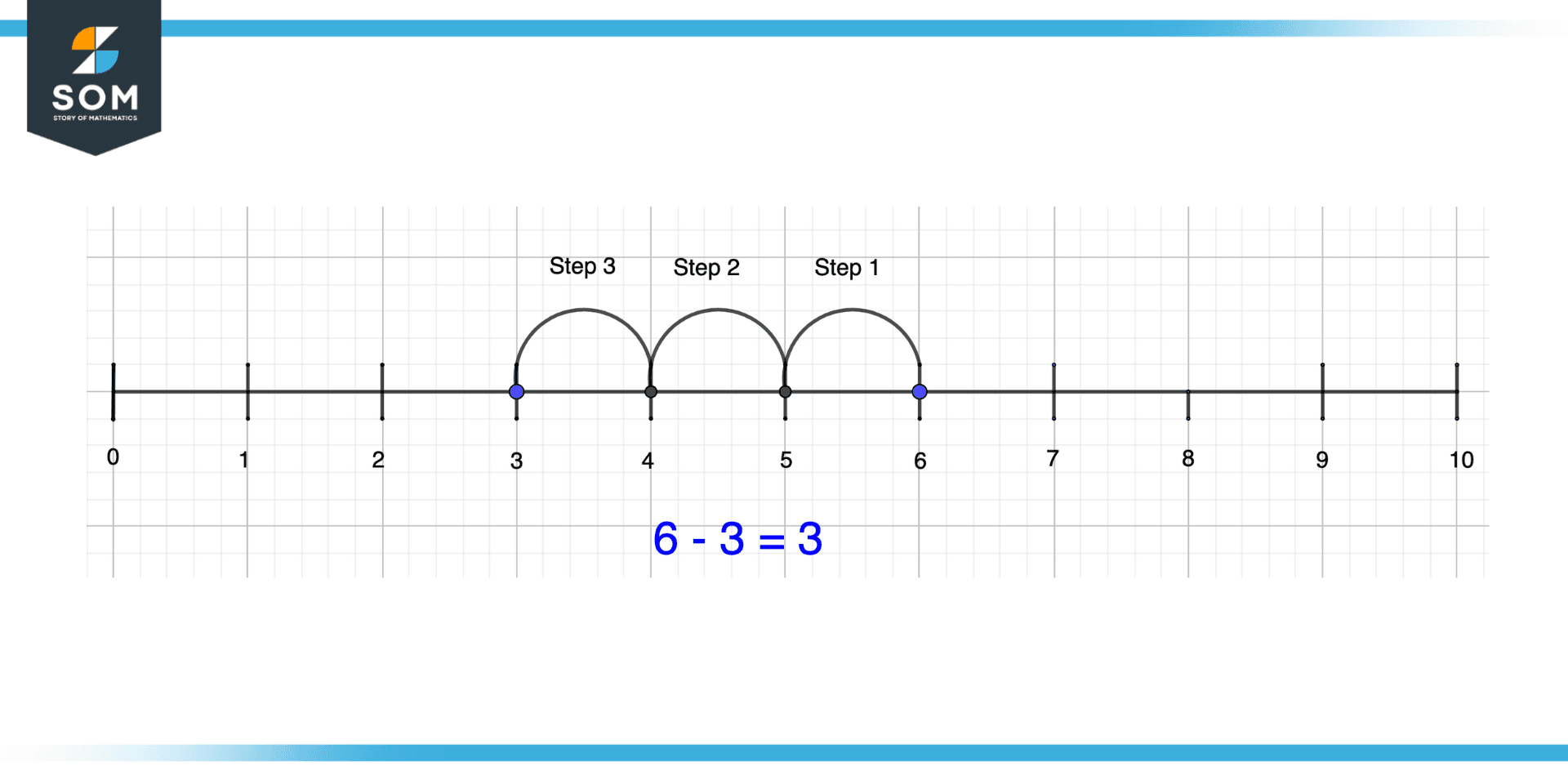
Figure 7 – Subtraction of Positive Numbers on Number Line

The Direction of Movement for Addition and Subtraction of Positive Numbers

For the addition of two numbers, we will move toward the right side while for the subtraction of two numbers, we will move toward the left side. Keep in mind the fact that the number line increases as we move toward the right side, and decreases as we move toward the left.

Addition of Negative Numbers on the Number Line

The concept of adding a negative number is the same as that of a positive number but with the change that the negative number will be dealt in the left side of the origin i.e. in their domain.

Suppose we have to add -5 and -3. On the number line, we will first plot -3 which would be toward the left of the origin, and from -3, we will take 5 steps towards the left side. The position we end up in will be the result of the addition.

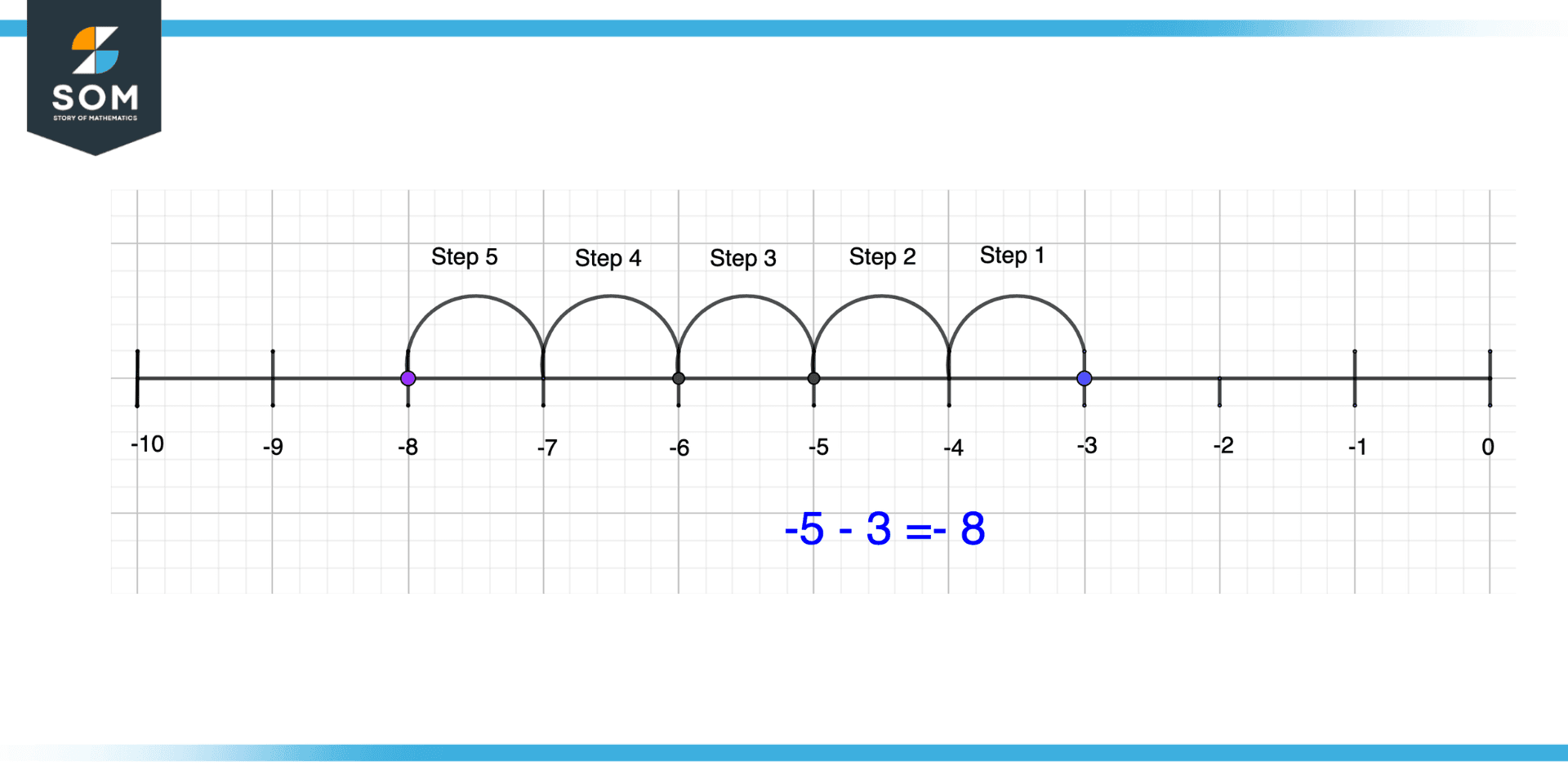
Figure 8 – Addition of Negative Numbers on Number Line

Subtraction of Negative Numbers on the Number Line

For the subtraction of two numbers -6 and -3, we will first plot the -6 number. Then, from the position of -6, we will take three steps toward the right side, and this position will be the result of the subtraction of these two numbers.

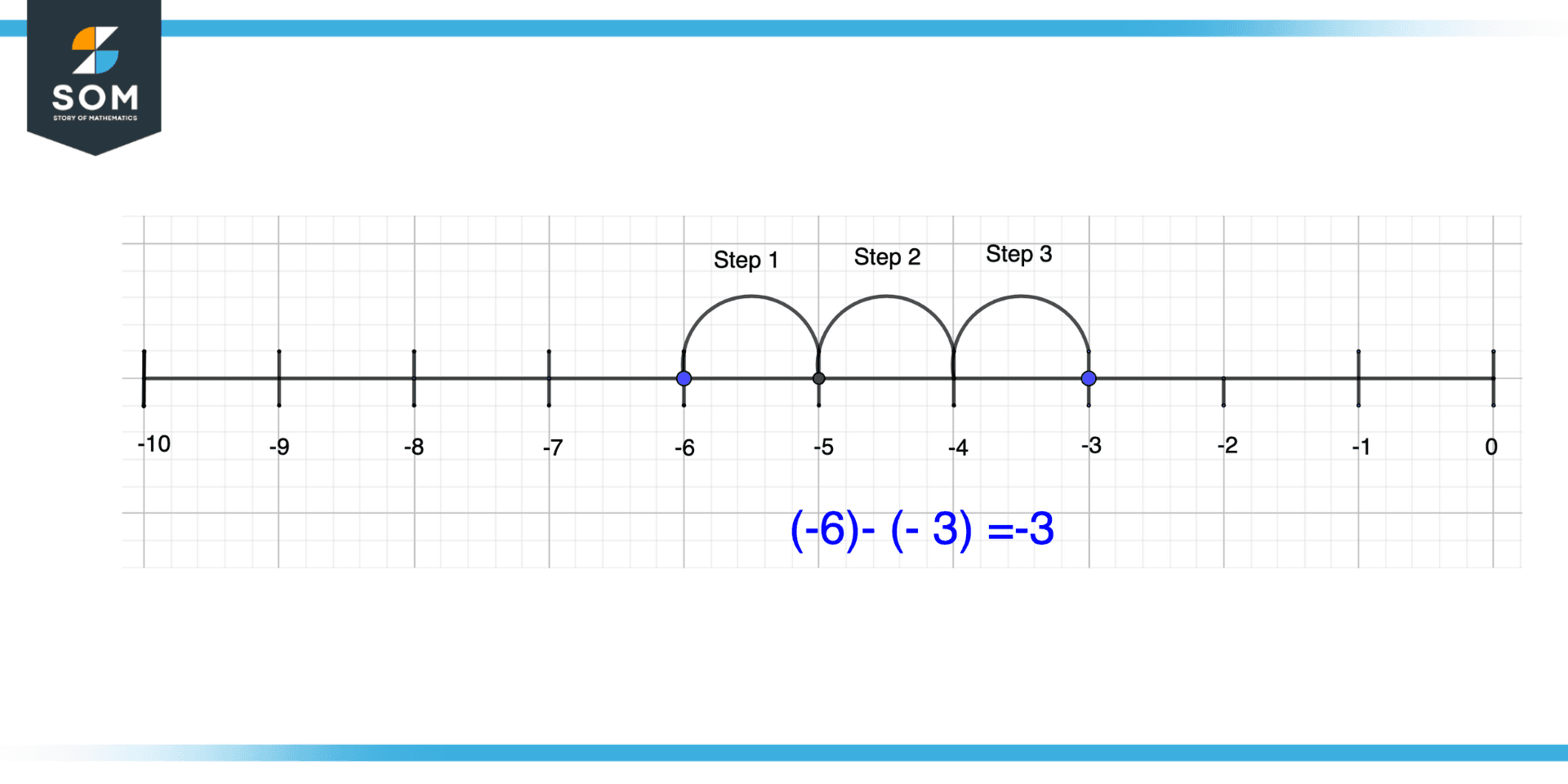
Figure 9 – Subtraction of Negative Numbers on Number Line

The Direction of Movement for Addition and Subtraction of Negative Numbers

For the addition of two negative numbers, we will move toward the left side, while for the subtraction of two negative numbers, we will move toward the right side. The interesting point to be noted here is that the direction of movement for negative numbers is opposite to the direction of positive numbers that we dealt with earlier.

A Solved Example Using the Number Line

Solve the following arithmetic problems graphically.

• 3+2
• 5-2
• (-3)+(-2)
• (-5)-(-2)

Solution

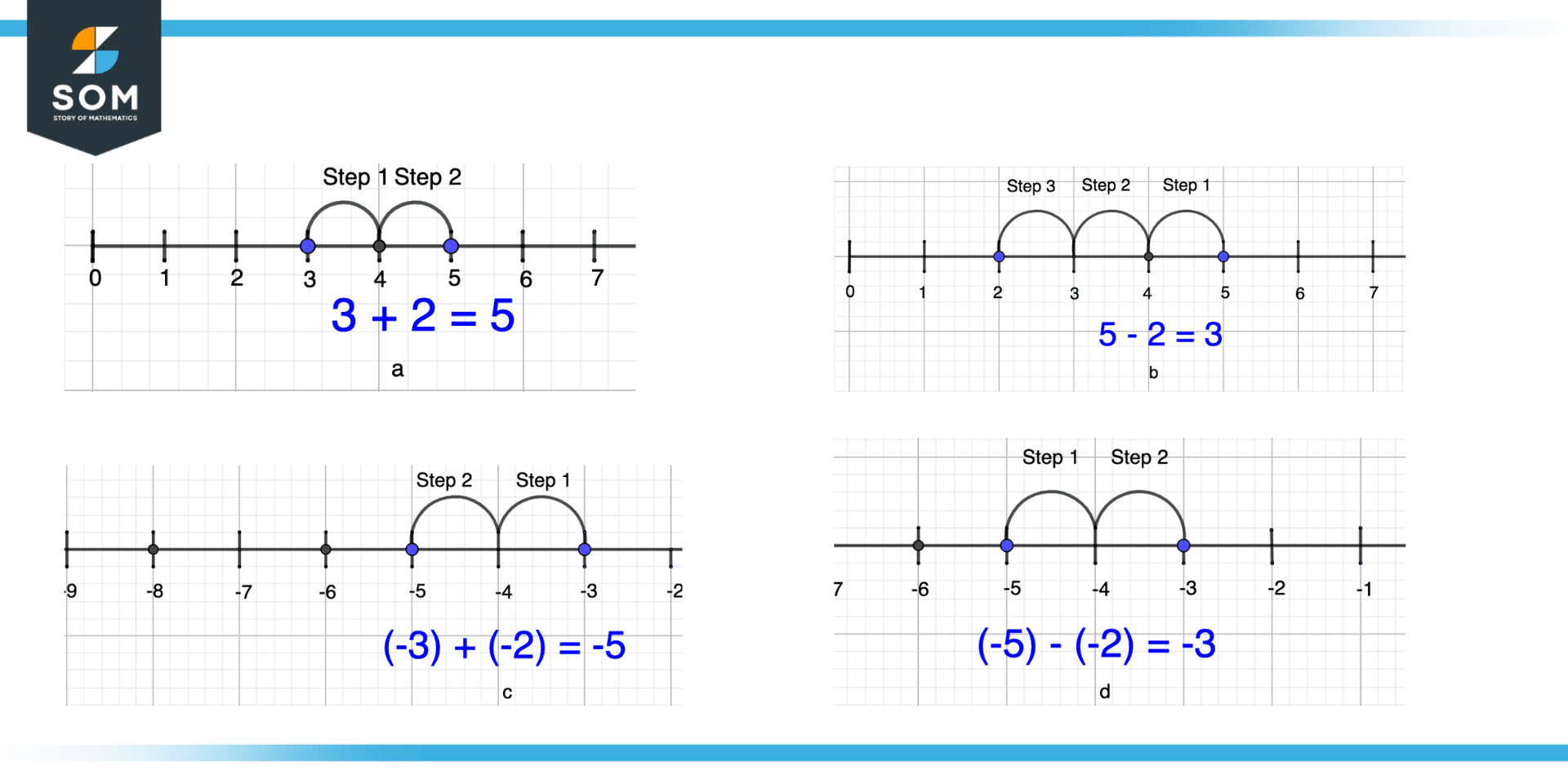
Figure 10 – Example of Number Line

All mathematical drawings and images were created with GeoGebra.

Notation Definition < Glossary Index > Numerator Definition