Notation|Definition & Meaning

What Is a Notation? 

It is more acceptable to communicate the lay of the field to someone who needs to navigate around regions. They are unaware of creating a map rather than using text because it is easier to understand.

Notation practice is based on the idea that symbols should represent particular concepts to facilitate clear and accurate communication. As an illustration, let’s look at the following two statements. The expressions ‘There are only four ways!’ and ‘The number of ways is only four!’ have entirely different meanings.

The first phrase needs to be clarified since there are four factorials (8!). Notation notes can be created more quickly than ever before.

Types of Notation

Words, characters, figures, and signs are the primary components that make up notation. The notation may use symbols, letters solely, numbers exclusively, or a combination of the two, such as the factorial symbol (n!). First, let’s have a look at some basic notation.

Notation Based on Counting

In your study of mathematics, you will most likely get familiar with the notation n! This is an illustration of the factorial.

n! = 1 if n = 0

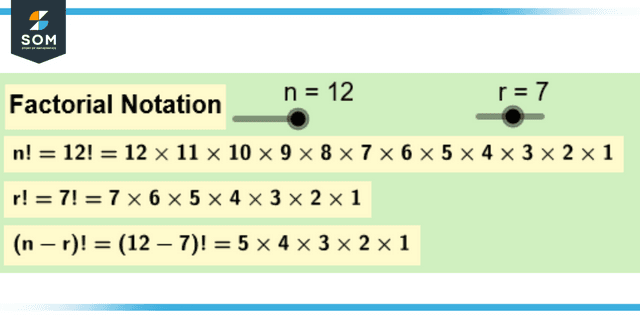
Figure 1: Representation of factorial notation.

Otherwise, the amount of different ways that n separate things can be arranged is what n! Counts. There is only one possible way to organize zero (0) items, which is to take no action.

The binomial coefficient notation is something that is associated with factorials. The count of k subsets contained within an n-set can be expressed using the above formula. Therefore, for the sake of this discussion, we will refer to n as a positive integer and k as a positive integer that is either smaller than n or equivalent to it.

Set Notation

Symbols are used in this system to define the components and characteristics of sets. We record our sets using the element notation and enclose them in curly brackets. For instance, declaring that 1, 2, and 3 are components of a set (S) whose elements are listed within curly brackets can be done by writing S = 1, 2, 3>, where the constituents of S are listed within the brackets.

Another possibility is that S equals 1, 2, 3,……, n. in this scenario version.

Alternatively, you may express the same idea as S = x |.

In the first phase, it is stated that the range of numbers from 1 to n is contained within a group known as S.

According to the second expression, a group known as S is equivalent to the members of x in such a way that x can take any value between 1 and n. The second expression does not contribute to understanding the number progression. The value of the variable x might be any number between 1 and n, such as 1.5. However, in the previous example, 1.5 is not a member of the list because it jumps directly from 1 to 2.

Therefore, the expression “member an exist or is a component or the collection / set A” is represented by the symbol “A.”

Various other items besides numbers can be included in sets as elements. You can chat about anything you would like to hear. For instance, if the set A is defined as “a, b, and c,” then the notation “an A” can be used to indicate that “a” is a component of “A.” Sets can be included as components in other sets. The fact that a. B is included in A can be denoted as a subset of A by using the notation a, b A.

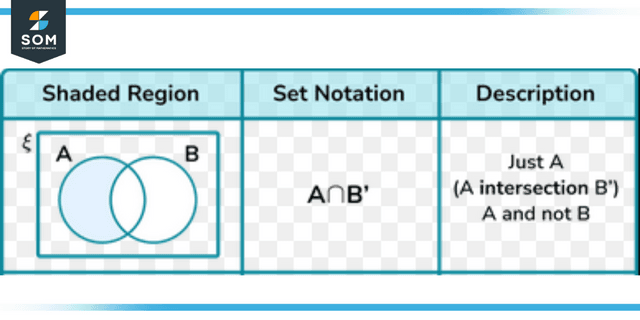
Figure 2: Representation of set notation.

Notation for Summarizing

A handy way to express lengthy sums is using summation notation. One possible representation of the mathematical expression 1 + 2 + 3 + 4 + 5 is the word. This indicates that we are adding up all of the different values of I, beginning with I = 1 and continuing until we reach I = 5, which is the point at which we stop.

Notation Using an Index

In mathematics, this type of notation is used to represent the representation of figures that multiply themselves a certain number of times.

By Using index notation 3, the number 3 can be written as, which is the same as the number 9. It can also be read as three raised to the power of two. When you hear the phrase “the number that is raised to the power of X,” the number X indicates the value of times that the base number doubles itself.

When it comes to expressing enormous numbers, index notation can also be helpful.

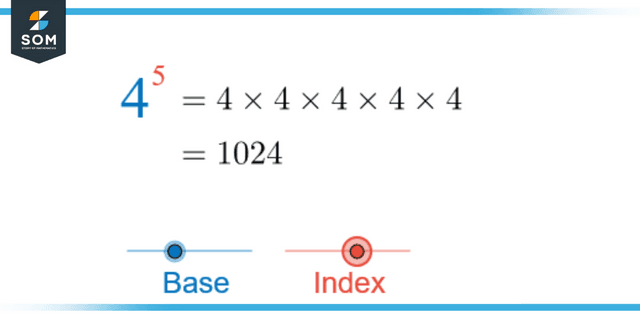
Figure 3: Representation of Index notation.

The Characteristics of the Notations

Notations need to have a few critical characteristics for them to be helpful.

• Uniqueness is a quality that establishes that a single notation can only ever stand for a single instance of something. This eliminates the possibility of harm caused by analogies and ambiguities in discrete mathematics.
• Clarity of notation is what we mean when we talk about expressivity. The correct notation needs to include all pertinent information written out in the precise manner in which it should be used. For instance, an index notation can be stated as the same as writing down the product of four times four. Writing the notation but omitting the power does not make it the same as the expression 4 multiplied by itself.
• The notations are as condensed and uncomplicated as humanly practical while maintaining their clarity. When writing lengthy ones, there is a greater likelihood of errors. Due to the high level of accuracy that is necessary for them to be considered genuine, it is imperative that they be simple to read, pronounce, and write.

Example 1

If (1/7!) + (1/8!) = (x/9!), find x.

Solution

(1/7!) + [1/(8*7!)] = [x/(9*8*7!)]

[(8+1)/(8*7!)] = [x/(9*8*7!)]

x = 81

Example 2

What is the intersection of the given sets?

U = {1,2,3,…,10}

A = {1,2,4,6}

B = {1,3,6,9}

Solution

A∩B = {1,6}

All images/graphs are created using GeoGebra.

Not Equal Definition < Glossary Index > Number Line Definition