Not Equal|Definition & Meaning

When a number does not have an equivalent in another number, we refer to that relationship as not equal. It is denoted by the symbol $\neq$, which consists of two horizontal lines that are parallel to one another and are cut by such an inclined vertical line. 

Explanation of Not Equal

Not equal is simple to understand because it represents a comparison of two numbers or quantities that are not equal. In everyday situations, we use them everywhere.

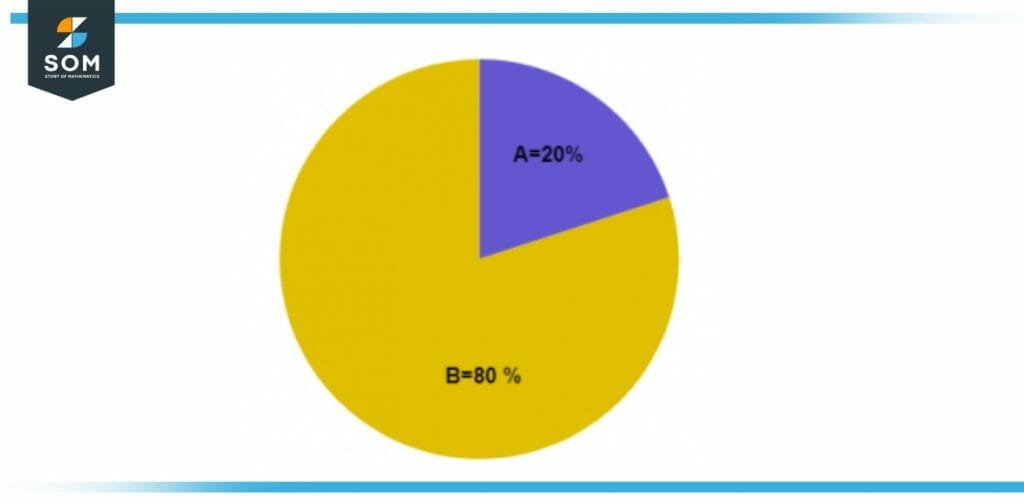
Figure 1 – Image of a circle split into two different unequal portions

The not equal term has a lot of applications in real-life scenarios. For example, John visited a fruit vendor in order to purchase 4 pounds of oranges. The fruit seller put them on his scale to see how much they weighed and he found that the weight of the orange was 8 pounds which is not equal to 4 pounds. Therefore  4 pounds are not equal to 8 pounds

Another situation where the use of not equal can be seen is if Alia needs to calculate the areas of squares with sides that are 2 inches and 5 inches long. She calculates the area of each square using the square formula, arriving at the conclusion that a square has a surface area of 4 square inches for sides that are 2 inches long and 25 square inches for sides that are 5 inches long. As a result, it can be that the two given squares do not have the same size.

Thus, you can now easily find the comparison between the two quantities or numbers which are not equal. The following figure represents the visual representation of not equal.

Visual Representation of Not Equal

We use the circle-based diagram below to illustrate the idea of not equal:

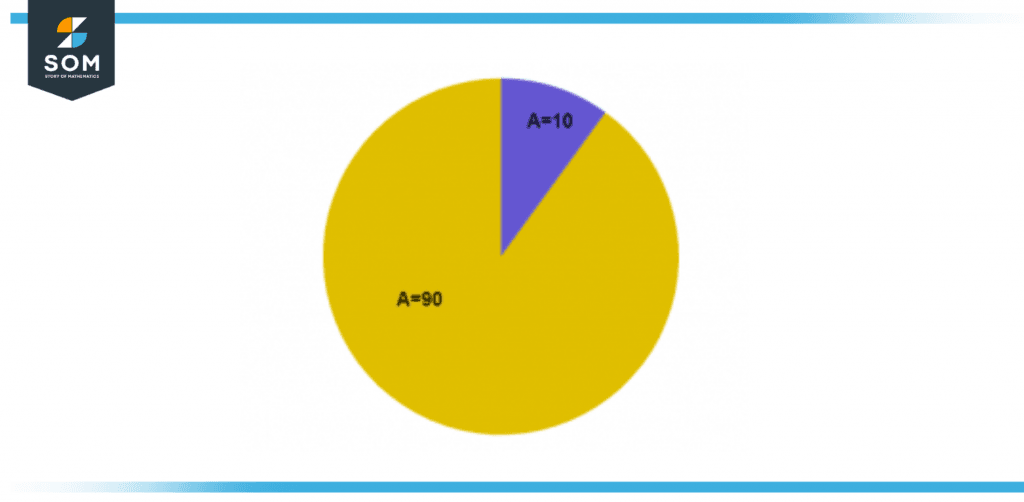
Figure 2 – Circle image split into two unequal portions

Suppose we have a circle and we split it into two unequal parts. The two unequal portions of A and B with values of 10 and 90, respectively, are depicted in the circle in Figure 2.

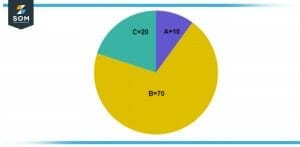
Figure 3 – Image of a circle split into three different unequal portions.

The circle in the above illustration is the result of splitting the circle into three unequal pieces. Three unequal portions of A, B, and C, with values of 10,70, and 20, respectively, are depicted in the circle in Figure 3.

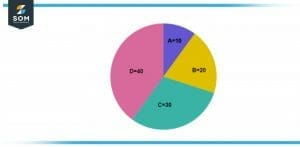
Figure 4 – Image of a circle split into four different unequal portions.

If we split the same circle with different values or unequal values of A, B, C, and D. We get a circle which is represented in figure 3. The values of A and B in this scenario are 10 and 20 respectively while the values of C and D are 30 and 40 respectively.

Numerical Example of Not Equal

The teacher of Adnan asked him to solve the two equations which are  4a+60 = 80, 5a +90=120, 5a + 90 = 140, 5a + 90 = 150, and 5a + 90 = 160. Determine whether or not an is equal to 2.

Solution

First, we have to find the value of a for the first equation. We are given  that:

4a + 60 = 80

So, we have to find the value of a. Subtracting 60 from both sides results in:

4a + 60 – 60 = 80 – 60

4a  = 80 – 60

4a = 20

Dividing 4 on both sides results in the following:

4a/4 = 20/4

a = 20/4

a=5

Therefore, it is concluded that the value of a is not equal to the given value of a. Thus 2 is not equal to 5.

Now, we have to find the value of a for the 2nd equation. We are given  that:

5a + 90 = 120

So, we have to find the value of a. Subtracting 90 from both sides results in:

5a + 90 – 90 = 120 – 90

5a  = 120 – 90

5a = 30

Dividing 5 on both sides results in the following:

5a/5 = 30/5

a = 30/5

a=6

Therefore, it is concluded that the value of a is not equal to the given value of a. Thus 2 is not equal to 6.

Now, we have to find the value of a for the 3rd equation. We are given  that:

5a + 90 = 140

So, we have to find the value of a. Subtracting 90 from both sides results in:

5a + 90 – 90 = 140 – 90

5a  = 140 – 90

5a = 50

Dividing 5 on both sides results in the following:

5a/5 = 50/5

a = 50/5

a=10

Therefore, it is concluded that the value of a is not equal to the given value of a. Thus 2 is not equal to 10.

Now, we have to find the value of a for the 4th equation. We are given  that:

5a + 90 = 150

So, we have to find the value of a. Subtracting 90 from both sides results in:

5a + 90 – 90 = 150 – 90

5a  = 150 – 90

5a = 60

Dividing 5 on both sides results in the following:

5a/5 = 60/5

a = 60/5

a=12

Therefore, it is concluded that the value of a is not equal to the given value of a. Thus 2 is not equal to 12.

Now, we have to find the value of a for the 5th equation. We are given  that:

5a + 90 = 160

So, we have to find the value of a. Subtracting 90 from both sides results in:

5a + 90 – 90 = 160 – 90

5a  = 160 – 90

5a = 70

Dividing 5 on both sides results in the following:

5a/5 = 70/5

a = 70/5

a=14

Therefore, it is concluded that the value of a is not equal to the given value of a. We can easily say that the two numbers are not equal. Thus 2 is not equal to 14.

All mathematical drawings and images were created with GeoGebra.

Normal Distribution Definition < Glossary Index > Notation Definition