JUMP TO TOPIC
Oblique Prism|Definition & Meaning
Definition
The word “oblique” means “slanting”. An oblique prism is a type of prism based on its alignment. It is a slanted or tilted prism as its bases are not perfectly aligned. Its lateral faces are parallelograms that do not form 90° angles with its base. The height of an oblique prism is measured externally and is not the height of the lateral face.
Figure 1 shows an oblique prism with height h which is the perpendicular length.
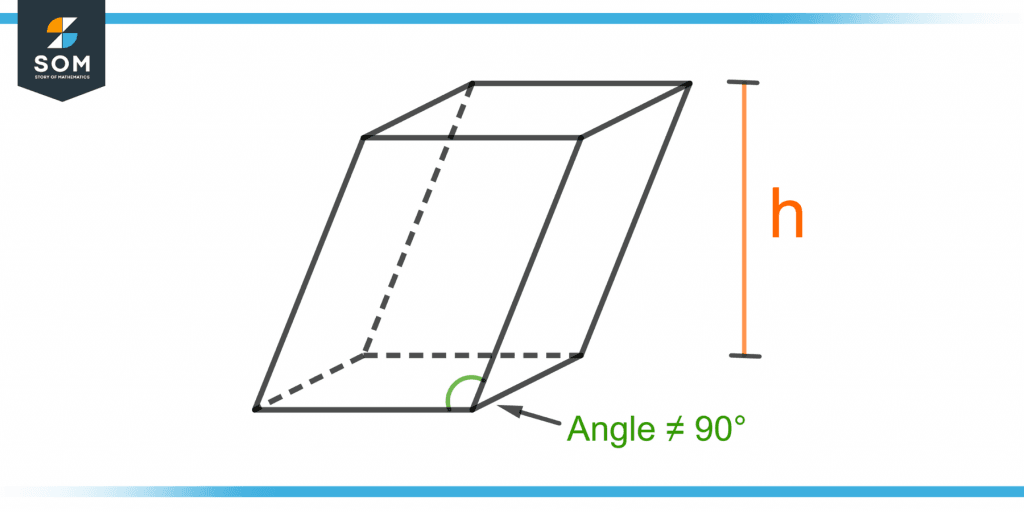
Figure 1 – An Oblique Prism with Height h
To understand an oblique prism comprehensively, first, we need to know about the “prism.”
Prism
A three-dimensional object with two same ends is known as a prism. It is a polyhedron with flat faces, straight edges, and sharp vertices. It has equal cross-sections with identical bases. The edges of a prism are parallel to each other, extending from one base to the other.
Base
The two bases are the two unique sides of a prism which defines the type of prism according to its shape. These bases are parallel to each other regardless the prism is right or oblique.
For example, a pentagonal prism has two pentagons as bases on each end of the prism.
Lateral Faces
A prism’s lateral faces are the faces that are on its sides instead of its top and bottom. The faces or sides of the oblique prism are parallelograms which is a four-sided polygon with parallel opposite sides.
Figure 2 shows a hexagonal oblique prism with a demonstration of its bases and lateral faces.
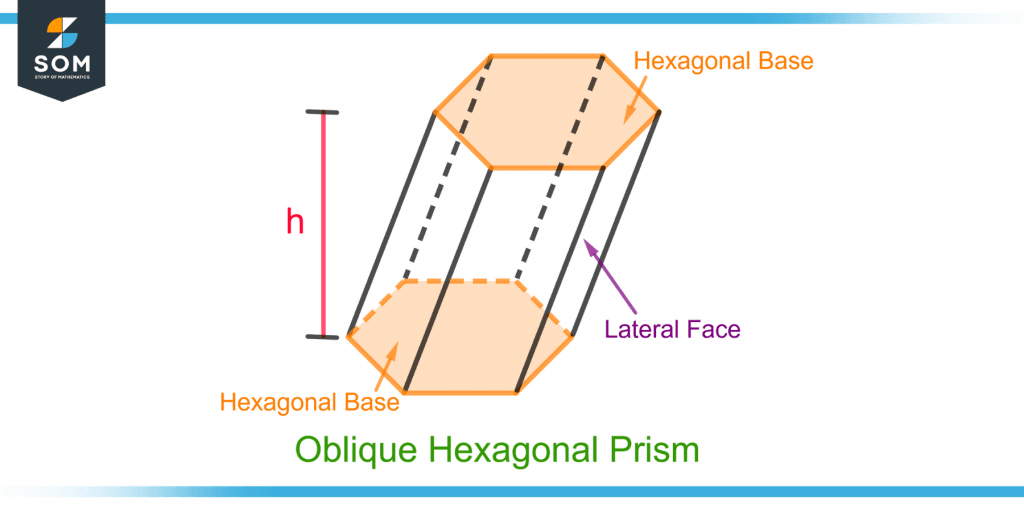
Figure 2 – Demonstration of the Bases and Lateral Faces of an Oblique Hexagonal Prism
Right Prism
A right angle is a 90° angle. A right prism is a type of prism in which the two bases and the lateral faces are joined by perpendicular lines. The base and the face form a 90° angle with each other. If a prism is not right, then it is oblique.
Figure 3 compares a pentagonal right prism and an oblique prism.
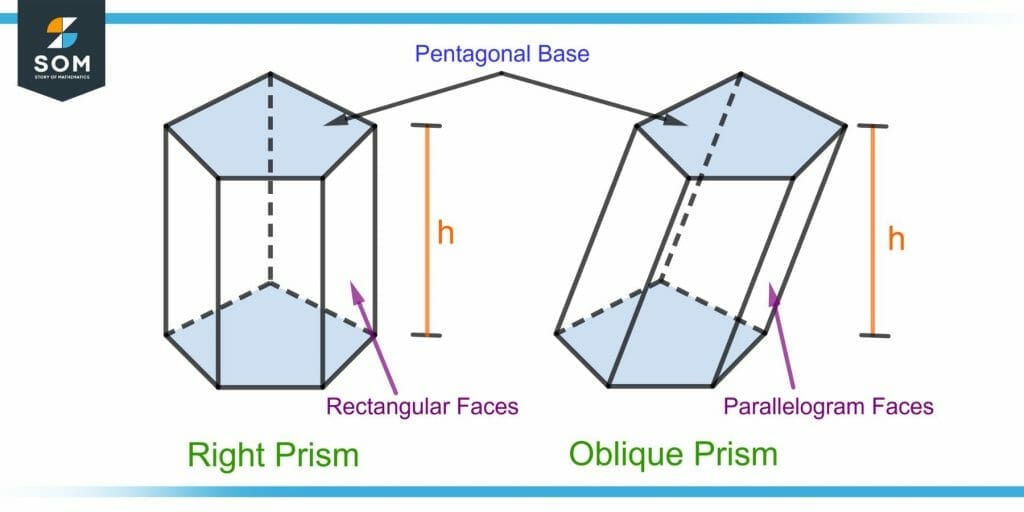
Figure 3 – Comparison of an Oblique and Right Pentagonal Prism
The bases of an oblique and a right pentagonal prism are the same; what’s different is the alignment of the two bases with each other. A right prism has rectangular faces, whereas an oblique prism has lateral faces as parallelograms.
Notice that the height of a right prism is the same as the height of an oblique prism. To understand this, consider two decks of the same number of cards.
One deck aligned perfectly, and the other slightly tilted. Both piles of cards will have the same height. Hence, the height of an oblique prism is the perpendicular length, not the slanting one.
Surface Area of a Prism
A prism’s surface area is the area of the outer part of a prism. Its formula is:
Surface Area = 2(B) + P(l)
Where P is the base perimeter, B is the base area, and l is the prism’s length or height. The base area, base perimeter, and length of a rectangular prism are illustrated in figure 4.
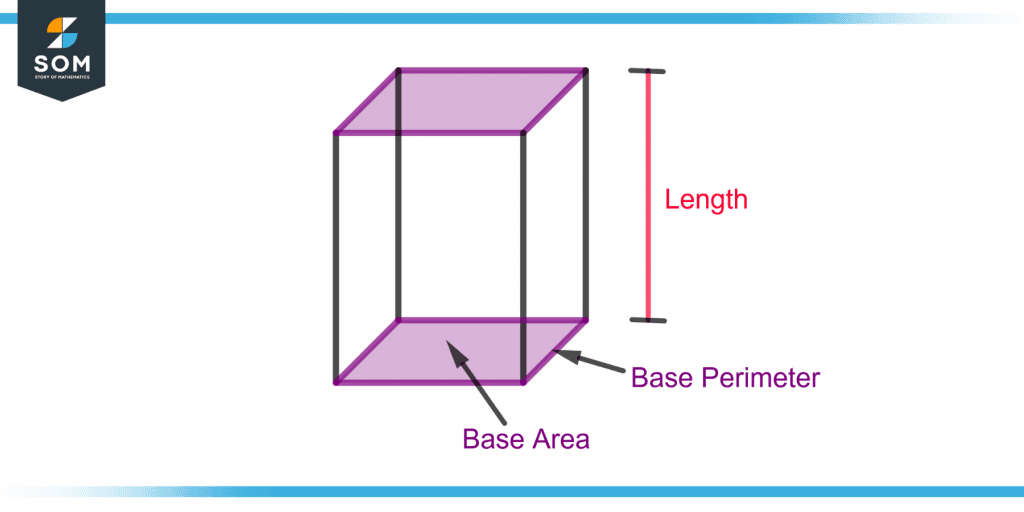
Figure 3 – Illustration of Length, Base Area and Base Perimeter of a Rectangular Prism for Surface Area
The surface area of an oblique prism is not easy to calculate. It is not common practice to calculate the surface area of an oblique prism as there is no direct formula.
Volume of an Oblique Prism
The volume is the space occupied by a solid object. The formula for a prism’s volume is as follows:
Volume of Prism = h.B
Where h is the height and B is the Area of the base of the prism. The SI unit of volume is cubic meters.
An oblique prism’s volume is equal to the volume of a right prism if both have the same bases. This is because both have the same perpendicular height.
Volume of Different Types of Oblique Prisms
Different types of prisms have different bases and hence have different base areas. By knowing the base area, one can calculate the volume. The volume of different kinds of oblique prisms is discussed below:
Square Prism
A square prism has a square as its base which has four equal sides. A cube is also a form of a square prism. The Base Area of a square prism is given by:
Base Area = s ✕ s = $s^2$
Where s is the length of the side of the square base.
The volume of an oblique and non-oblique square prism is:
Volume = $s^2$ ✕ h
Rectangular Prism
A rectangular prism has a rectangular base. A rectangle is a quadrilateral having equal opposite sides. If the length of the rectangle is L and the width is W, then its base area is given as:
Base Area = L ✕ W
So, a rectangular prism’s volume will be:
Volume = L ✕ W ✕ h
Triangular Prism
A triangular prism has a triangle as its base. A triangle is a three-sided polygon whose three angles sum to 180°. If the base of the triangle is B and the height is H, then its base area is:
Base Area = B.H / 2
Then, the triangular prism’s volume will be:
Volume = (B.H ✕ h) / 2
Figure 5 shows oblique square, rectangular and triangular prisms with their dimensions.

Figure 5 – Different Types of Oblique Prisms and Illustration of their Dimensions
Examples
Example 1
Find the volume of an oblique, rectangular prism of height 16 cm. The length of the rectangular base is 10 cm, and its width is 6 cm.
Solution
A rectangular prism’s volume is given as:
Volume = L ✕ W ✕ h
An oblique, rectangular prism has the same volume as a right rectangular prism. Here:
L = 10 cm, W = 6 cm, h = 16 cm
Putting the values in the above equation gives:
Volume = 10 ✕ 6 ✕ 16
V = 960 cm$^3$
So, the volume of the oblique, rectangular prism is 960 cubic centimeters.
Example 2
The volume of an oblique, triangular prism is 400 cubic meters, and its height is 16 m. If the length of the triangular base is 10 m, what is the height of its base?
Solution
The volume for an oblique, triangular prism is given as:
V = (B.H ✕ h) / 2
Multiplying 2 on both sides gives:
2V = B.H ✕ h
Dividing B.h on both sides gives the equation for the height of the triangular base H as:
H = 2V / B.h
Here:
V = 400 cubic meters, B = 10 m, h = 16 m
Putting the values in the above equation gives:
H = 2(400) / 10(16)
H = 800 / 160
H = 5 m
So, the height of the triangular base of an oblique prism is 5 m.
All the images are created using GeoGebra.
