JUMP TO TOPIC
Oblique Pyramid|Definition & Meaning
Definition
An oblique pyramid is a pyramid with an oblique base and one whose apex is not parallel to the base. To put it another way, the base is angled or inclined with respect to the apex. This indicates that the pyramid’s sides are not parallel to its base and do not intersect at a straight angle.
Overview of Pyramids
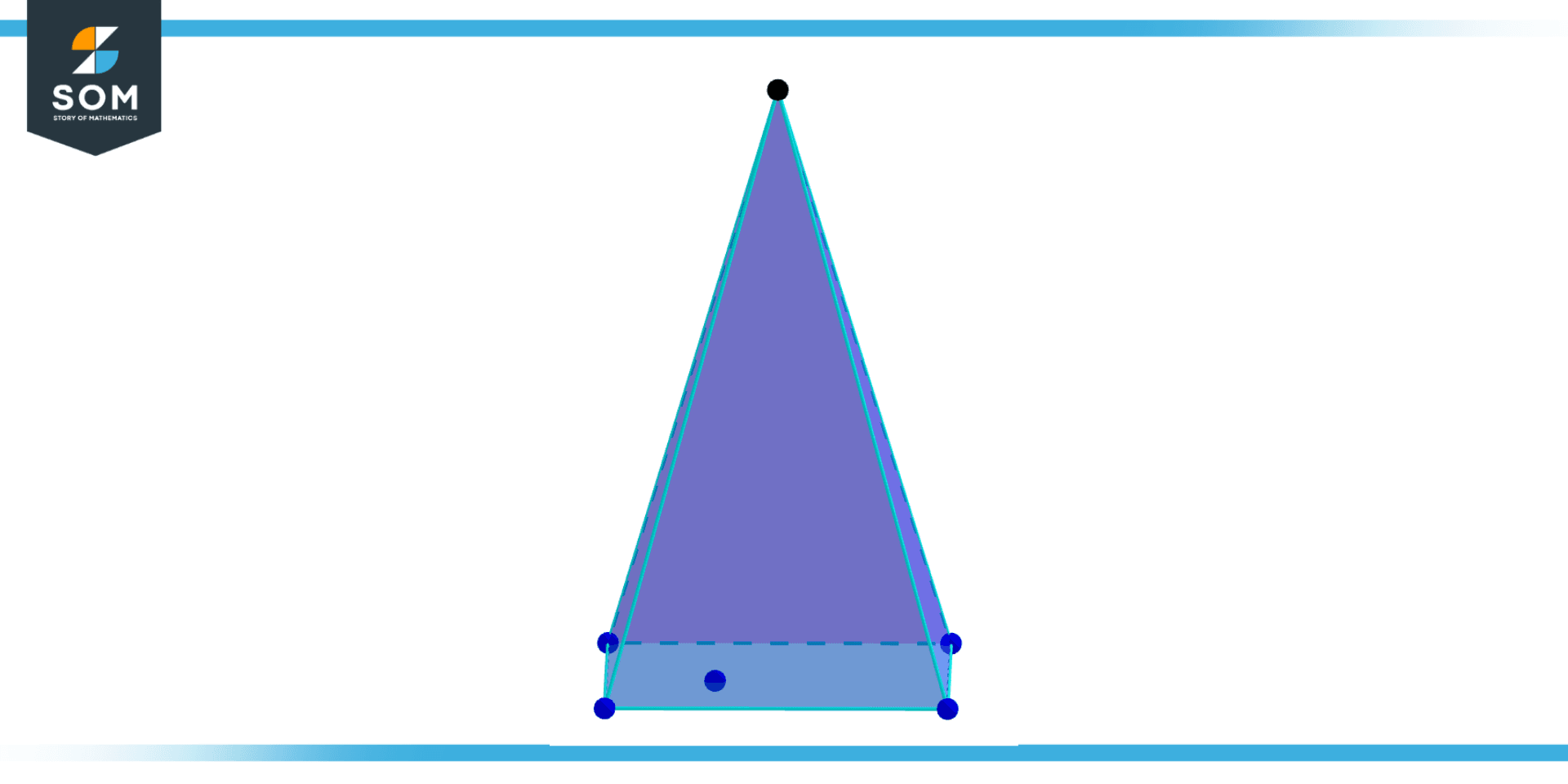
Figure 1 – Visualization of Pyramid
A pyramid is a three-dimensional geometric object having triangular sides meeting at a single point at the top, known as the apex, and a polygonal base. Any polygon can serve as a pyramid’s base, but triangles and quadrilaterals are the most frequent choices. Pyramids are given names based on the shape of their bases; for example, a triangular pyramid is known as such, whereas a quadrilateral pyramid has a foundation that is quadrilateral.
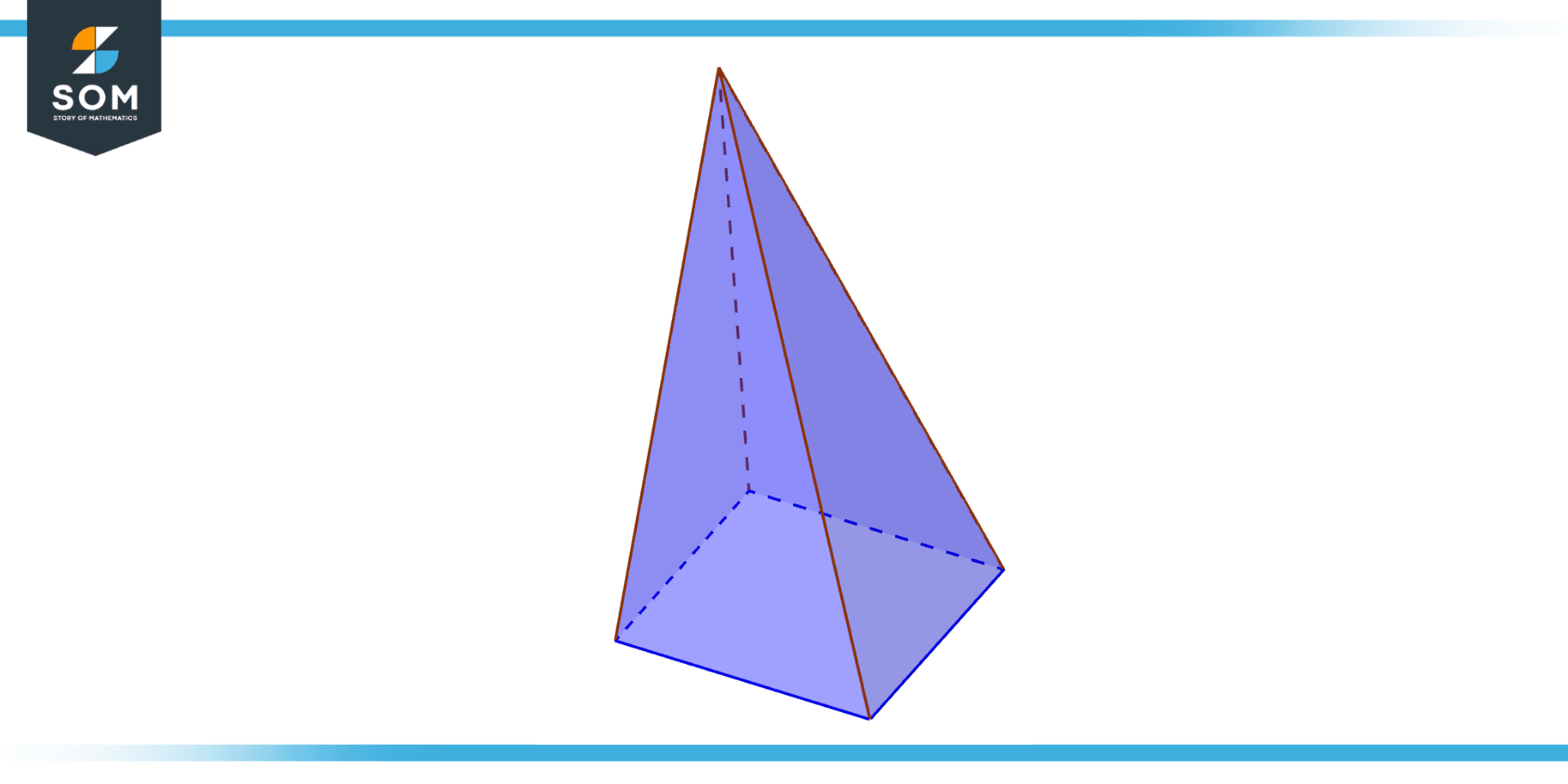
Figure 2 – Illustration of Oblique Pyramid
A pyramidal structure with a base that isn’t parallel to the ground is called an oblique pyramid. A pyramid turned on its side can be used to describe it. An oblique pyramid has a base that can be any quadrilateral shape, and its sides are triangles. The intersection of the sides forms the peak of an oblique pyramid.
Formulae for a Few Concepts in Oblique Pyramid
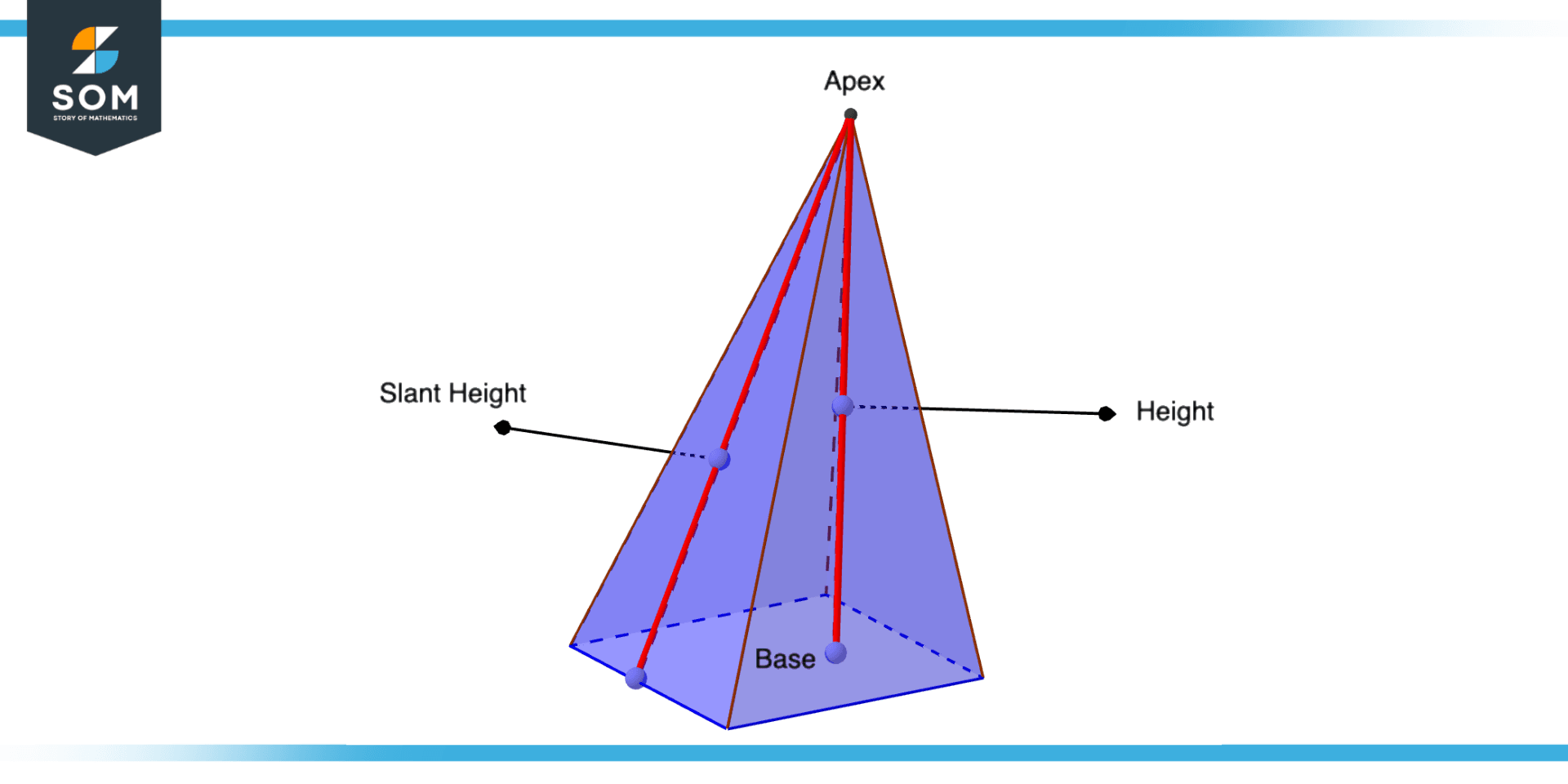
Figure 3 – Labelling of Oblique Pyramid
Volume
An oblique pyramid’s volume is given by the formula:
volume = $\dfrac{\text{base area} \times \text{height}}{3}$
Surface Area
By calculating the area of each of the triangular faces and then putting them together, one can determine the surface area of an oblique pyramid. The base is the area of the quadrilateral basis, whereas the lateral surface area is the area of all the triangular sides.
Lateral Area
The lateral area of an oblique pyramid is the sum of the areas of all the triangular faces. It can be calculated using the formula
lateral area = $\dfrac{\text{perimeter of base} \times \text{slant height}}{2 }$
where the slant height is the distance from the apex to the edge of the base.
Lateral Edge
The lateral edge of an oblique pyramid is the distance from the apex to the edge of the base(lateral faces). It can be calculated using the Pythagorean theorem
lateral edge = $\sqrt{(\text{height})^2 + (\text{base edge})^2}$
Slant Height
The slant height of an oblique pyramid is the distance from the apex to the edge of the base. It can be calculated using the formula
slant height = $\sqrt{(\text{lateral edge})^2-(\text{height})^2}$
Diagonal
The diagonal of an oblique pyramid is a line segment connecting two non-adjacent vertices of the base. It can be calculated using the Pythagorean theorem:
diagonal = $\sqrt{(\text{base edge})^2 + (\text{height})^2}$
Median
A median of an oblique pyramid is a line segment connecting a vertex of the base to the midpoint of the opposite edge. It can be calculated using the formula
median = $\dfrac{\sqrt{2(\text{base edge})^2 + (\text{height})^2}} { 2}$
The Angle Between the Lateral Edge and Base
The angle between the lateral edge and the base can be calculated using the formula
angle = $\arctan{\left(\dfrac{\text{height}}{\text{base edge}}\right)}$
The Angle Between the Lateral Face and Base
The angle between a lateral face and the base can be calculated using the formula
angle = $\arcsin{\left(\dfrac{\text{base edge}} {\text{lateral edge}}\right)}$
The Angle Between the Diagonal and Base
The angle between a diagonal and the base can be calculated using the formula
angle = $\arccos{\left(\dfrac{\text{base edge}} {\text{diagonal}}\right)}$
Properties of Oblique Pyramid
Some properties of the oblique pyramid are given below:
- The base of an oblique pyramid isn’t parallel to the ground.
- An oblique pyramid’s base can be any quadrilateral shape, but a rectangle is the most typical choice.
- An oblique pyramid has triangle sides that converge at a single point known as the apex.
- The perpendicular distance from an oblique pyramid’s apex to the base plane is how tall it is.
- The formula (base area * height) / 3 can be used to get the volume of an oblique pyramid.
- By calculating the area of each of the triangular faces and then putting them together, one can determine the surface area of an oblique pyramid. The base is the area of the quadrilateral basis, whereas the lateral surface area is the area of all the triangular sides.
- An oblique pyramid has vertices in the corners of the base and an apex.
- An oblique pyramid has triangles for its sides and a polygon for its base.
- The segments separating the vertices on an oblique pyramid are known as its edges.
- The faces of an oblique pyramid are flat surfaces with borders enclosing them.
- An oblique pyramid’s face count is influenced by the base’s side count.
Difference Between Oblique Pyramid and Right Pyramid
Here are the main differences between an oblique pyramid and a right pyramid.
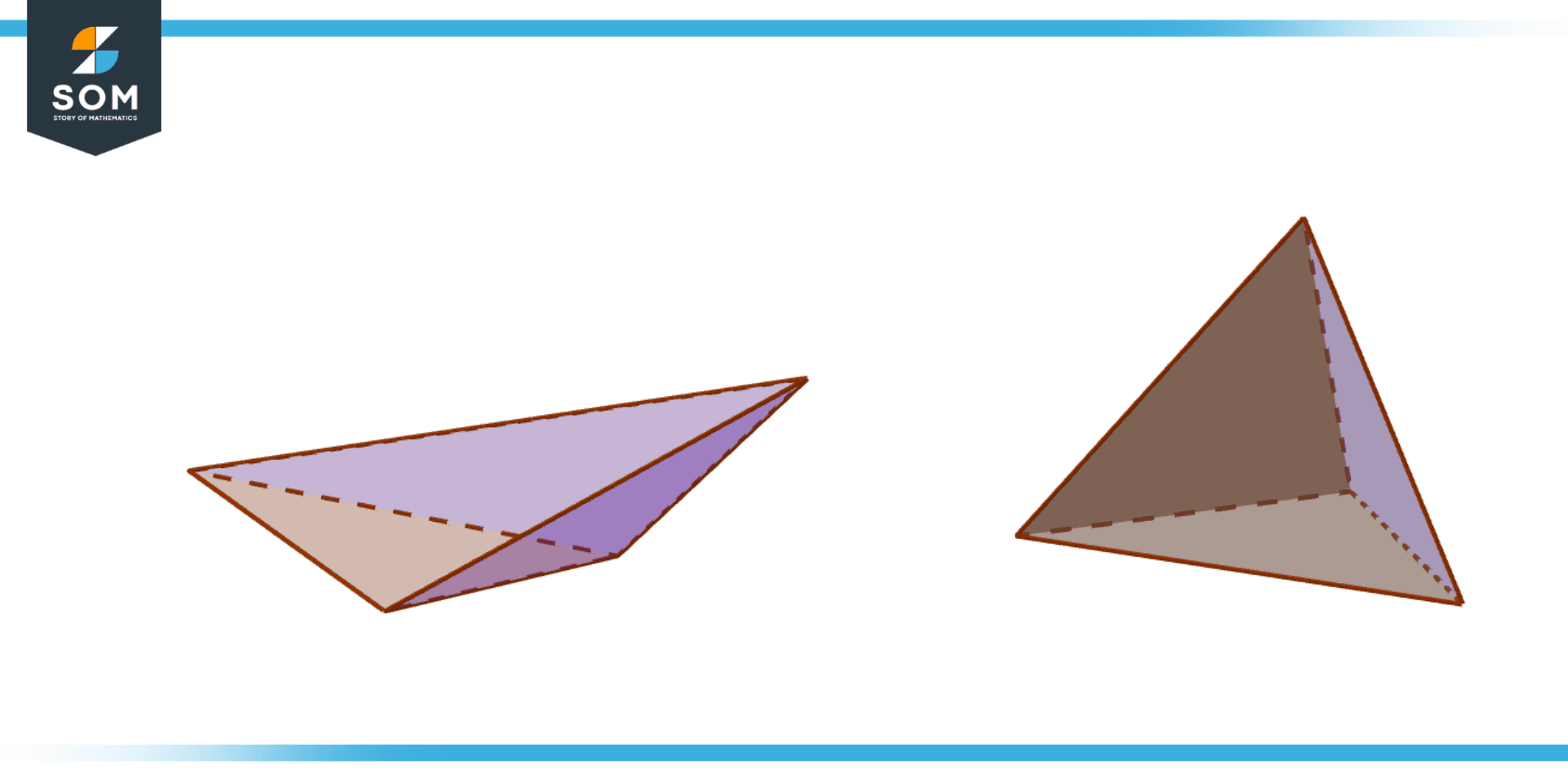
Figure 4 – Illustration of Oblique Pyramid and Right Pyramid
- Base Orientation: Right pyramids have bases that are perpendicular to the apex, while oblique pyramids have bases that are inclined at an angle to the apex.
- Shape: A right pyramid has a normal, symmetrical shape, whereas an oblique pyramid has a distorted shape with sloping sides.
- Calculating the volume of an oblique pyramid: The volume of an oblique pyramid is determined using the formula V = (Bh)/3, where h is the pyramid’s slant height. The same method is used to get the volume of a right pyramid, however here, h stands for the pyramid’s height.
- Calculating an oblique pyramid’s surface area: The surface area of an oblique pyramid is determined using the formula S = B + (1/2)pl, where l is the pyramid’s slant height. A right pyramid’s surface area is computed by adding the base’s area to the total of its triangle faces.
- Examples from the actual world: Oblique pyramids are less frequent in real-world applications than right pyramids. Oblique pyramids are utilized less frequently than right pyramids, which are employed for a variety of purposes, such as storage tanks and silos.
Practical Example
Example
Imagine we have an oblique pyramid with a base that is a hexagon with side lengths of 8 cm. The apex of the pyramid is located 12 cm above the center of the base. Find the Slant Height of the Oblique Pyramid.
Solution
First, we need to find the slant height of the pyramid. The slant height is the distance from the apex to the base along the lateral edge of the pyramid. We can use the Pythagorean Theorem to find the slant height:
\[l^{2} = h^{2} + \left(\frac{B}{2}\right)^{2}\]
\[l = \sqrt{h^{2} + \left(\frac{B}{2}\right)^{2}}\]
\[l = \sqrt{12^{2} + \left(\frac{8}{2}\right)^{2}}\]
\[l = \sqrt{144 + 32}\]
\[l = \sqrt{176}\]
\[l = 13.6 \text{ cm}\]
All mathematical drawings and images were created with GeoGebra.
