JUMP TO TOPIC
Obtuse Angle|Definition & Meaning
Definition
In geometry, an obtuse angle is one with a value larger than 90 degrees but less than 180 degrees. The phrase “an angle with measurement exceeding 90 degrees but less than 180 degrees is termed an obtuse angle.” To put it another way, an obtuse angle is one that falls in the middle of a right angle and a 90-degree angle.
One of the triangle’s angles is obtuse. Hence, this type of triangle is called an obtuse triangle. There is no such thing as a triangle that is composed entirely of obtuse angles because that would not even qualify as a shape called a triangle. Obtuseness is a property that can only be shared by only one angle in a triangle.
Degree of Obtuse Angle
According to what we studied in the section that came before this one, an obtuse angle is one that has a measurement that is fewer than 180 degrees but greater than 90 degrees. 165 degrees, 135 degrees, 110 degrees, 179 degrees, 91 degrees, and so on are all examples of obtuse angles. As a result, the degree of obtuse angle falls somewhere between the ranges of 90 and 180 degrees.
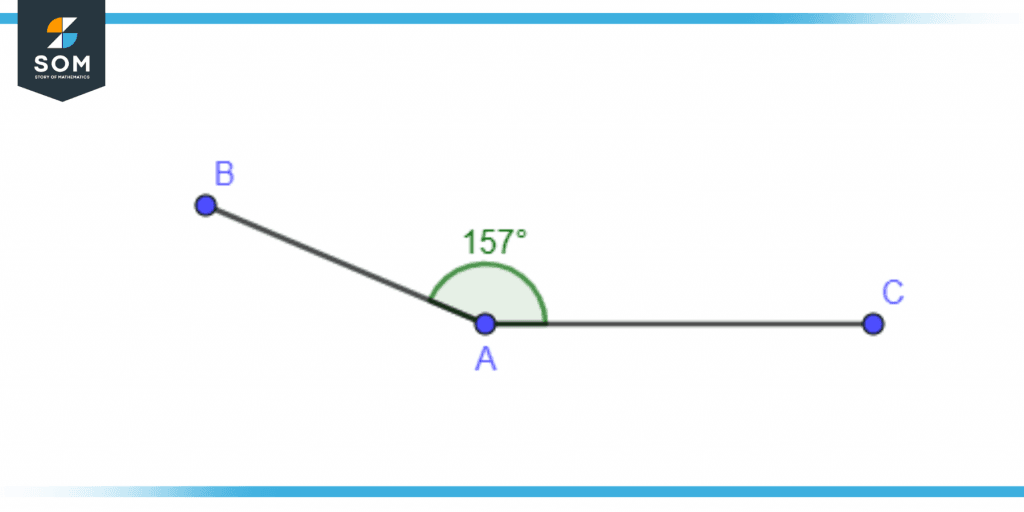
Figure 1 – Obtuse Angle
These angles have a measurement that falls between 90 and 180 degrees.
A right angle, which measures 90 degrees, is greater than an acute angle, whose measurements is fewer than 90 degrees, but an obtuse angle, which measures less than 180 degrees, is less than a straight line angle which is 180 degree. On the other hand, if we list the angles from smallest to largest measurement, the order would be as follows: acute, right, obtuse, and straight.
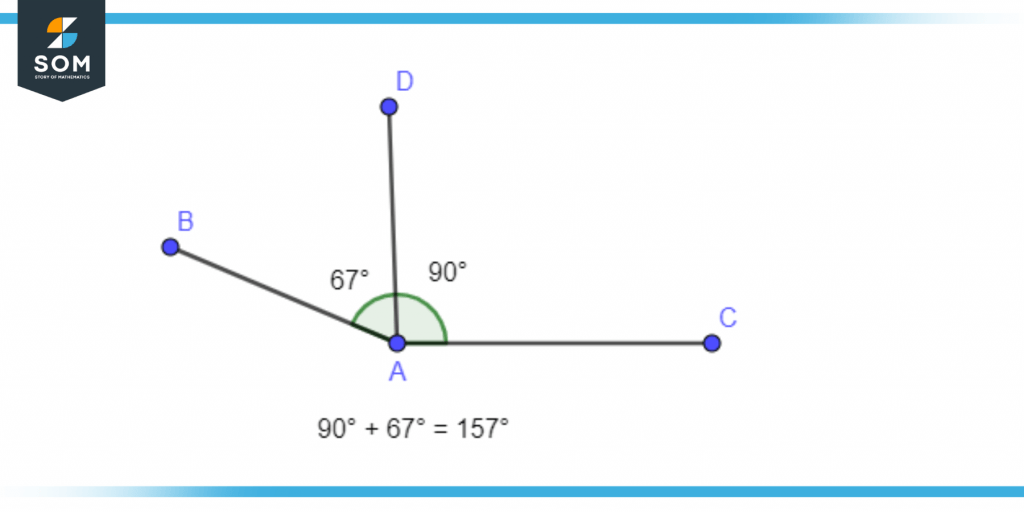
Figure 2 – Obtuse Angle of 157 Degree
This angle represents greater than a circle quarter yet fewer than a circle half when viewed visually. Therefore, if we cut a circle into quarters, an obtuse angle always will fill between one-fourth and one-half of the circle when we do this.
Within the confines of an obtuse triangle, there is invariably an angle that is obtuse.
Obtuse Angle In Triangle
A triangle with an obtuse angle is a type of triangle that is defined by having one of its vertex angles that is more than 90 degrees. You can have an isosceles triangle or a scalene triangle when you have an obtuse triangle. It is impossible for a triangle with equal sides to have an obtuse angle.
The side of the triangle that is perpendicular to an obtuse angle is the largest of the three of that particular triangle.
According to the property of the sum of the angles of the triangle, there is no way for there to be both an obtuse angle and a right angle within the same triangle at the same time.
Therefore, we are able to draw the conclusion that if one of the angles that make up a triangle is an obtuse angle, then the remaining two angles that make up a triangle should be acute angles.
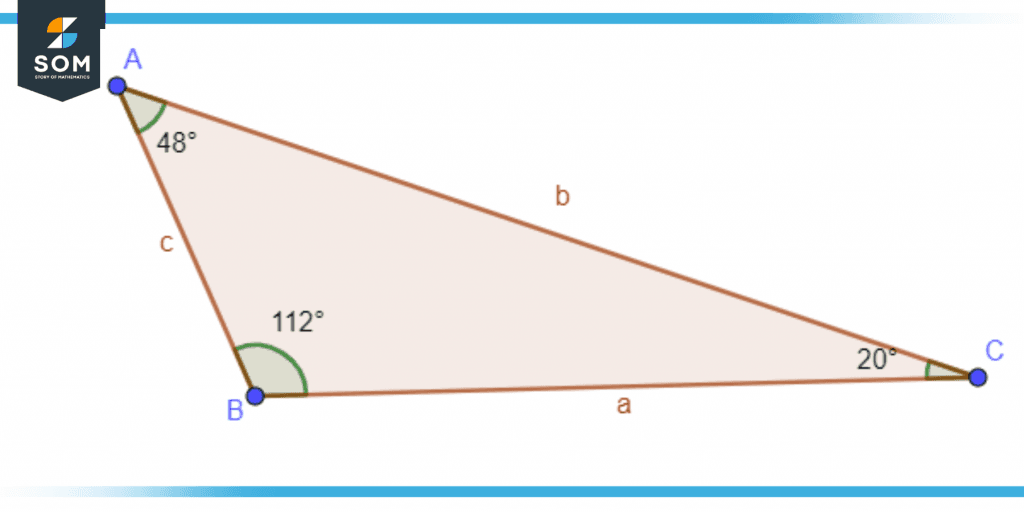
Figure 3 – Obtuse Angle In Triangle
One of the triangles up top has an angle that is larger than ninety degrees. Because of this, we refer to them as obtuse-angled triangles or just obtuse triangles for short. The square of the addition of two triangle sides is less than that of the square of the triangle’s longest side because an obtuse angle triangle has an acute angle. Since the sides of the triangle ABC have the measurements 48 degrees, 112 degrees, and 20 degrees, respectively, and a is the longest side.
Obtuse Angles in Polygons
A polygon with obtuse angles can be classified into two distinct subtypes: those that have just obtuse angles and those that have a minimum of one acute angle. The former category is more typical, whereas the latter category is notoriously challenging to put together.
In a polygon with obtuse angles, the sum of the individual angles will almost never add up to less than 180 degrees. This is due to the fact that the combined degrees of a triangle’s angles equal 180 °, and a polygon with an obtuse angle must contain a minimum of one triangle.
A polygon with obtuse interior angles will have interior angles, all of which are under 180°. This is due to the fact that an obtuse angle has a degree measurement that is more than 90° but lower than 180°.
Every one of the obtuse angle polygons’ outside angles is larger than 180°. This is due to the fact that the total of all the angles in the polygon is always 360°, and a polygon with an obtuse angle always contains at least one angle that faces the outside of the shape.
Example 1
Show the obtuse angle in a triangle.
Solution
Here in the figure below, a triangle ABC is shown.

Figure 4 – Obtuse Angle In Triangle
This scalene triangle has all unequal sides, so the angles are also unequal. It can be clearly seen that at point A, the angle is 48°. Likewise, at point C, the angle is 20°. Both these angles are less than 90°, so these are acute angles. In contrast to this, at point B, the angle is 112° which is greater than 90° but less than 180°. Therefore, this is the obtuse angle.
Example 2
Show that a regular polygon has all obtuse interior angles.
Solution
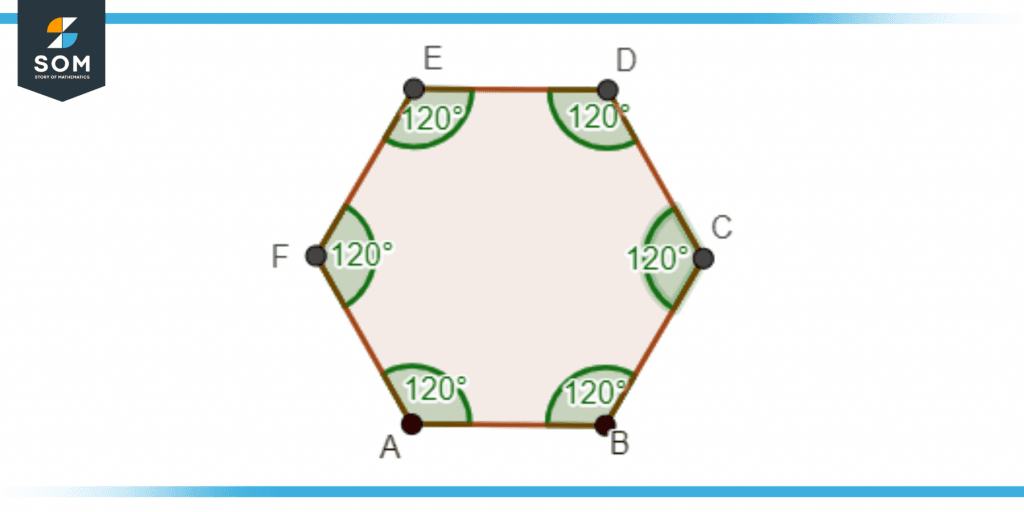
Figure 5 – Obtuse Angle In Regular Polygon
In this example, a regular hexagon is shown, which has six equal angles, each of 120°. The exterior angle of each side of the hexagon is 60°, and the interior angle is 120°. All the angles are 120° which is obtuse because it is greater than 90° and less than 180°, so a regular hexagon has all obtuse angles present inside it.
All the figures above are created on GeoGebra.
