JUMP TO TOPIC
Oblique|Definition & Meaning
Definition
Oblique is the geometrical position of a line or plane that is neither parallel nor perpendicular to the reference ground or line. All the positions with reference points that are not at 0 degrees, 90 degrees, 180 Degrees, 270 degrees, and 370 degrees are referred to as oblique.
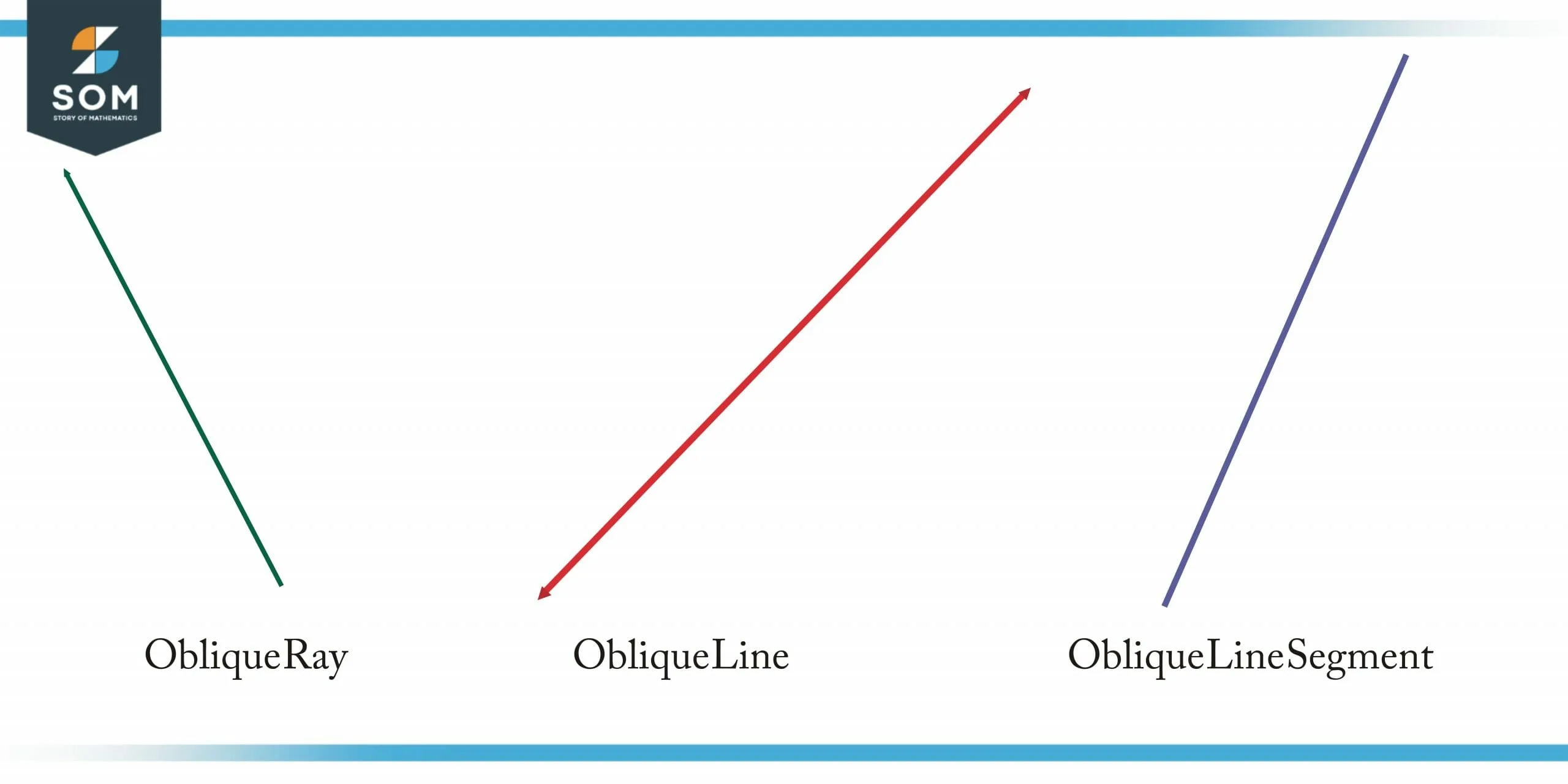
Figure 1 – Oblique Ray, Oblique Line and Oblique Line Segment
Oblique Lines
The oblique line is a line that lies in the same plane but is neither parallel nor perpendicular.
Oblique Angles
Oblique angles are angles that are not right angles or multiples of right angles. As a result, the sides forming the angle can’t be perpendicular.
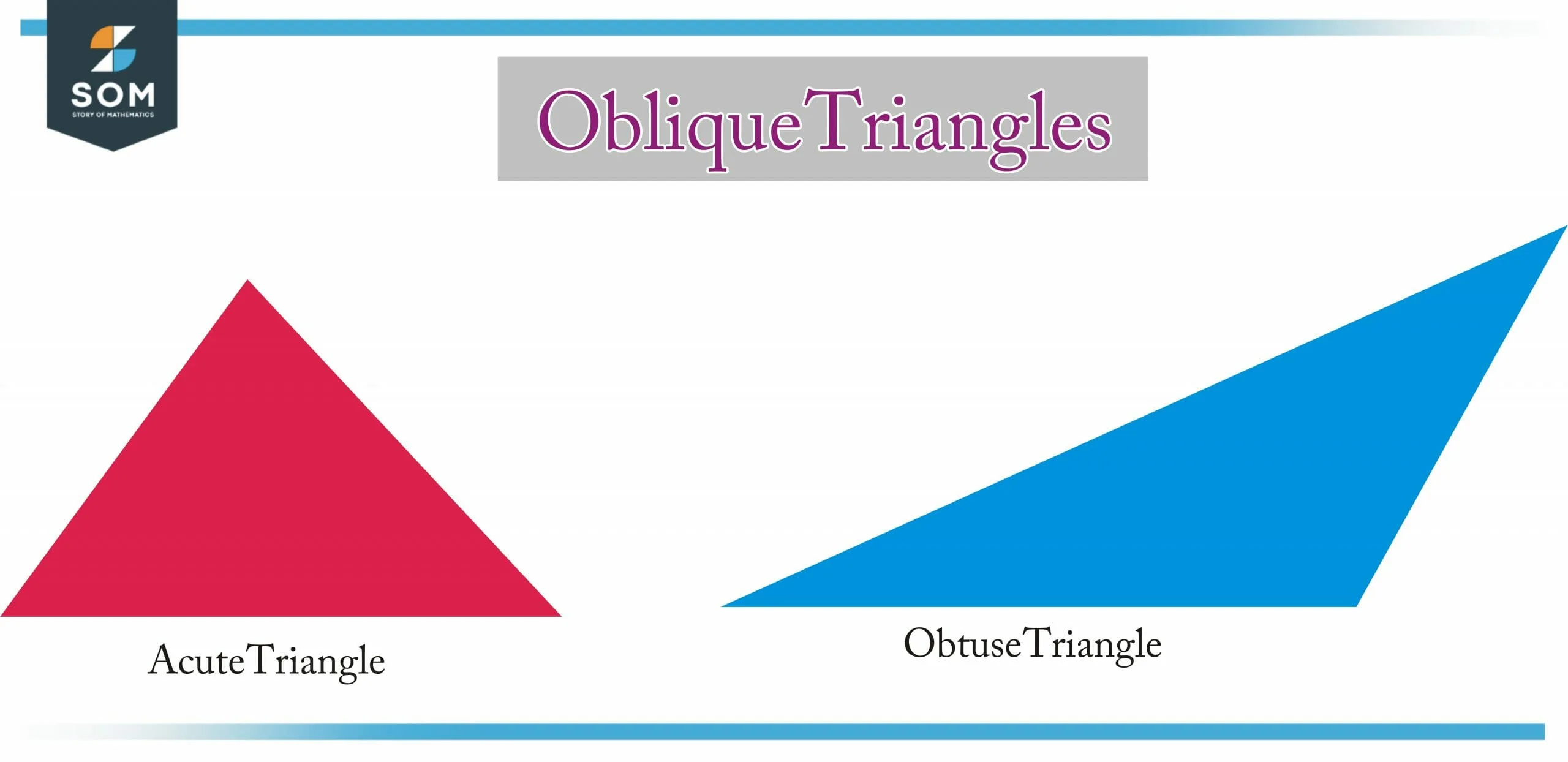
Oblique Triangle
The interior angle of an oblique triangle is not a right angle. There are two types of oblique triangles, acute triangles, and obtuse triangles.
| Acute Triangle | Obtuse Triangle |
In an acute triangle, the angle measures less than 90 degrees on each side. A perpendicular line is drawn from the base to the opposite vertex of the triangle. | In an obtuse triangle, there should be at least one angle greater than 90 degrees. The centroid and in-center lie inside an obtuse triangle, while the Circumcentre and Orthocentre are located outside of it. |
Figure 2 – Oblique Triangles
Oblique Prisms
Oblique prisms have lateral faces that are not perpendicular to their bases. Therefore, when the prism rests on its base, the two bases are not perfectly aligned. A prism’s lateral face is not its height. From outside the shape, a prism’s height is calculated.
Formulas to Calculate the Surface Area and Volume of Oblique Prisms
Surface Area 0F Oblique Prisms
Using the formula below, we can calculate the surface area of an oblique prism as two times the base area plus the areas of the parallelograms:
Surface area=2 × base area + area of each parallelogram
Oblique prisms have parallelogram-shaped lateral faces, and the lateral faces may be congruent or incongruent depending on the prism shape. In general, calculating the surface area of an oblique prism is not a common practice since there is no direct formula for calculating it.
The Volume of Oblique Prisms
Volume is the space occupied by an oblique prism in a three-dimensional space. Having the same height as a right prism, the volume of the oblique prism is the same as the volume of a right prism with the same height. To measure the volume, the units that are used are m3, cm3, mm3, and ft3.
Here is the formula for calculating the volume of an oblique prism:
The volume of prism= base area of prism × height of the prism
Oblique Cylinder
An oblique cylinder has circular bases and sides that are not perpendicular to each other. In other words, the two bases of an oblique cylinder are parallel but not directly aligned. Therefore, an oblique cylinder has sides that lean over at an angle other than 90°. An oblique cylinder is thus exactly opposite to that of a right cylinder.
Formulas To Calculate the Volume and Surface Area of an Oblique Cylinder
Having the same height as a right prism, the volume of the oblique cylinder is the same as the volume of a right circular cylinder with the same height. To measure the volume, the units that are used are m3, cm3, mm3, and ft3.
Here is the formula for calculating the volume of an oblique cylinder:
Volume of an oblique cylinder= πr2h
Surface Area of Oblique Cylinder
The surface area of an oblique cylinder also has two types as that of a right circular cylinder. The following are discussed below with formulas.
Lateral (Curved) Surface Area
An area formed by the curves on a cylinder’s surface is known as the curved surface area or lateral surface (LSA). Thus, it refers to the space that lies between the two circular bases that are parallel to each other. LSA is calculated by using the following formula:
LSA of oblique cylinder = 2πrl
Where π =22.7, r= radius, l=length.
The Total Surface Area of an Oblique Cylinder
The area that is occupied by the entire cylinder is known as the total surface area of an oblique cylinder. This area consists of two circular bases and one curved surface. An oblique cylinder’s TSA can be calculated by using the following formula:
TSA of oblique cylinder = 1 + 2πr2
Oblique Sketching
An oblique sketch depicts the perspective of an object in three dimensions through a pictorial representation. It is possible to do this type of drawing either in a normal, cabinet, or cavalier style. A sketching of this type is usually used by marketing departments to illustrate the product and its features to their customers in their business process.
Our everyday lives are filled with several objects that are three-dimensional, such as prisms, basketballs, footballs, etc., and we come across them all the time. The representation of a three-dimensional object on a two-dimensional plane can be easily accomplished by using an oblique sketch.
Difference Between Oblique Sketching and Isometric Sketching
The following table highlights the differences between oblique and isometric sketching.
| Oblique sketching | Isometric sketching |
| Oblique sketching focuses on the front view or the face of the object. | While isometric sketching focuses on the edge of the object. |
| Third dimensions are usually rendered with a 45-degree angle. | The angles are usually drawn at 30 degrees. |
Advantages of Oblique Sketching
Oblique sketching draws circular lines in true shape and size that are parallel to the projection’s front plane. Consequently, we may say that in this case, the circular features appear to be in the form of a circle rather than an ellipse.
There are three axes on which the oblique sketches are constructed, that is, a horizontal axis, a vertical axis, and a receding axis which can vary between 300 and 600 from the horizontal.
Real-life Example
Are you familiar with the Leaning Tower of Pisa? Hundreds of years ago, a tower was built in Pisa, Italy. The building began to lean over time. Could you call it the Oblique Tower of Pisa?

Figure 3 – Leaning Tower of Pisa
Yes, because it leans at an oblique angle to the ground.