Oblique Cone|Definition & Meaning

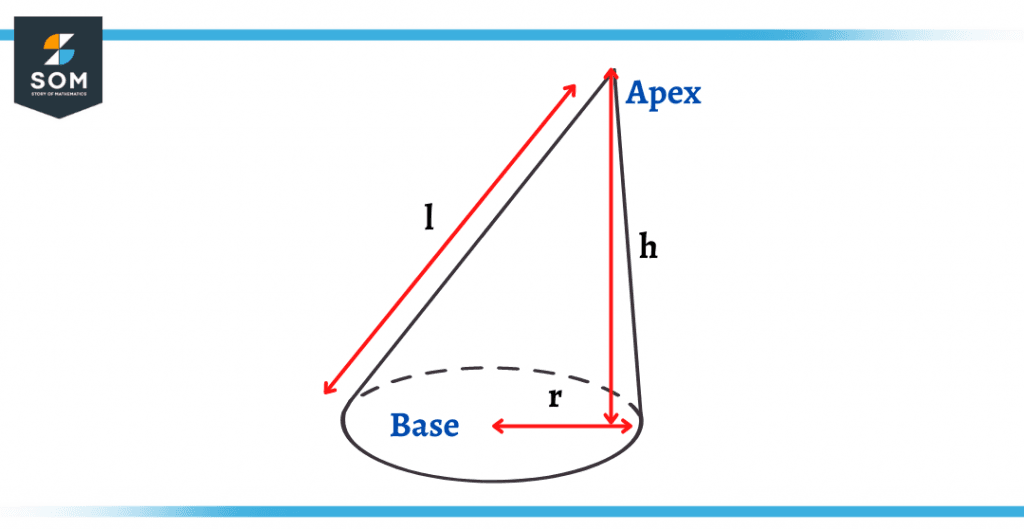
Figure 1 – An Oblique Cone With Base Radius r, Height h, and Slant l

A right cone would have a circular base and a closed-shaped axis from its vertex, which would direct towards the center of the circular base, or the axis would pass through the center of the base. 

The vertex of the cone lies directly above the central point of the circular base. The reason it is called a right cone is because of the angle that the axis makes with the radius of the circular base. The axis forms a right angle; therefore, the term “right” is used.

On the other hand, the oblique cone also contains a right angle, but it is not in line with the central point of the circular base.

What Is a Cone?

A cone is defined as a three–dimensional triangle having two faces, a circular base, and a curved face that tightens slickly from a flat circular base to the vertex (tip of the cone). A pyramid is also a kind of cone with a triangular cross-section, whereas a cone is defined by a circular cross-section. Such cones having a circular cross-section are known as circular cones.

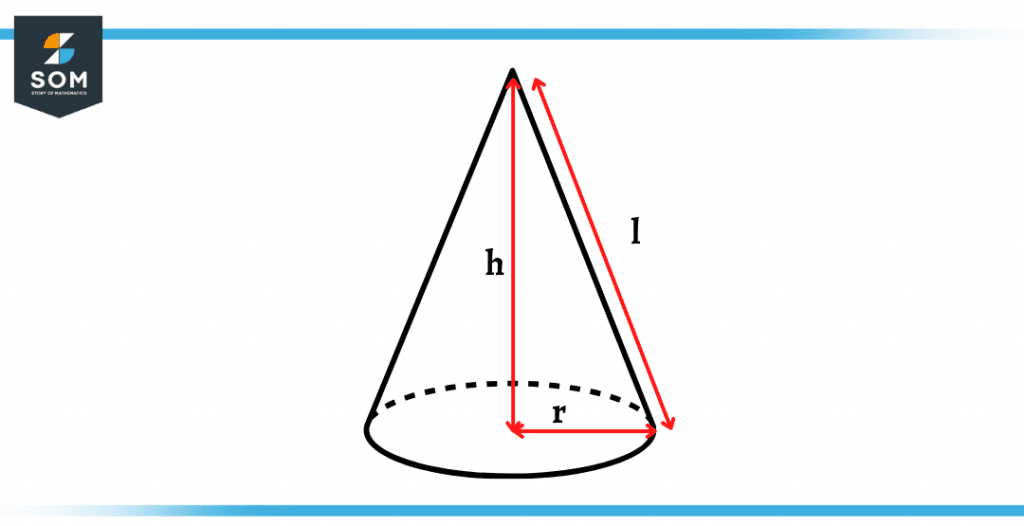
Figure 2 – A Right Cone with a height perpendicular to the base radius

The unique shape of a cone is formed by a set of infinite line segments or the lines that converge at a common point, as we called it the apex or vertex, and connects this point with all the infinite points on the circular base circumference.

The perpendicular distance from the vertex of the cone to the circular base is known as the height of the cone.

Since the base is a circle, the measured values will be of radius. In contrast, the tilted distance from the vertex to any point from the infinite points on the circular circumference is known as the slanted height.

We can measure the area of the circular surface and the overall volume of the cone using these terms. All these terms are shown in figure 2 given above.

We can easily find various cone-shaped objects and tools existing in our households, locations we work, workshops, and many more. Some include birthday party cones, waffle ice cream cones, traffic cones, chemical funnels, etc.

Measurements and Equations of an Oblique Cone

Slant Height of Cone

As discussed above, the tilted distance from the edge of the cone to any point on the circumference of the circular base is known as the slant height. In the case of an oblique cone, the vertex does not come perpendicular to the center of the circle, so the height of the cone has to be calculated with respect to the same base, keeping the angle exactly equal to 90 degrees.

The equation to find the slant height of a regular cone or an oblique cone can be easily derived with the help of the Pythagoras Theorem.

If we take ‘h’ as the vertical height of the cone, L as the slant height, r as the base radius, and d as the distance outside the base, we get a right-angled triangle, thus:

\[ l^2 = (2xr +d)^2 + h^2 \]

Slant Height l = $\sqrt{(2xr +d)^2 +h^2}$

Cone Volume

A good way to look at cones is to visualize a triangle that is being revolved around one of its vertices (preferably the farthest one). The volume of a cone can be calculated using a simple example, where we take a cylindrical container and a conical flask having the exact height and the exact base radius.

Now start filling up the conical flask until it is filled to the edge. Upon adding this water to the container, you will notice that the container takes up to 3 flasks to fill up. Thus the volume of the container is 3 times that of the volume of the cone, or the cone volume is one-third of that of the cylindrical container.

Now it becomes easy to derive the formula, that is, one-third times the area of the circular base times the height of the cone:

V = 1/3 $\times$ Circular base Area $\times$ Cone Height

Since the area of a circle is equal to $\pi r^2$  and the height of the cone is h, so:

\[ V = \dfrac{1}{3} \times \pi r^2 \times h\]

Here V is the volume of the cone, r is the base radius and h is the vertical height of the cone.

Surface Area of a Regular Cone

The Total surface area of the cone is equal to the circular base area plus the lateral surface area. The lateral surface area of the cone is $\pi rl$ and the surface area of the base is $\pi r^2$, thus:

Total Surface Area of the Cone = $\pi rl + \pi r^2$

Area = $\pi rl + \pi (l + r)$

Elliptic Cone

An elliptic cone is a type of cone having an elliptical cross-section. The elliptic cone is defined by its directrix which is in the form of an ellipse. The only difference between this and a regular circular cone is the circular cross-section in its shape. The elliptic cone is a quadric surface also known as a degree two cone because of its two angles at the vertices.

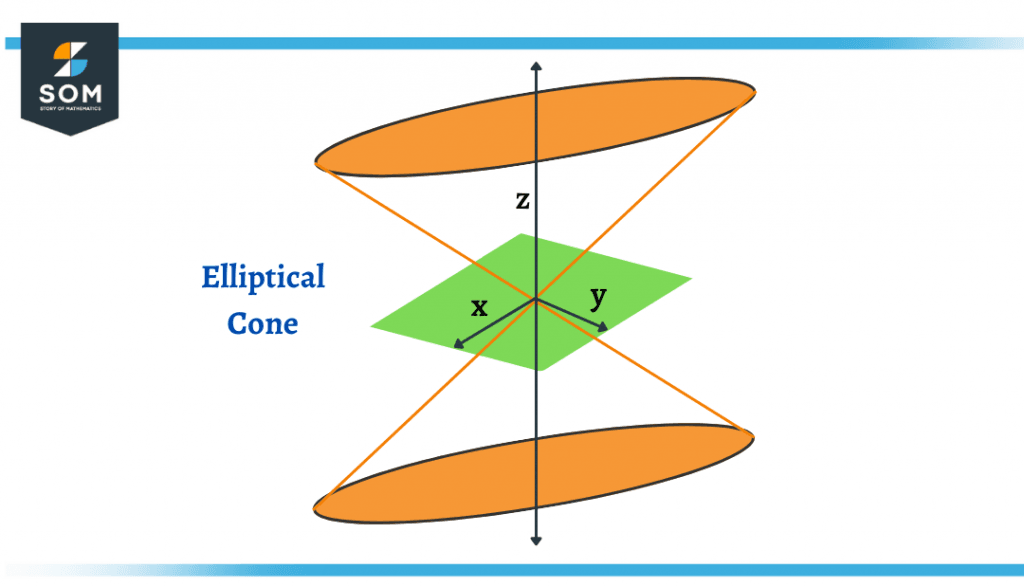
Figure 3 – Elliptic Cone

Properties of an Oblique Cone

• A cone will only contain one flat face and a round slanted face.
• The circular base narrows down to only one edge called the vertex.
• A cone can only contain one vertex.
• The total volume of a cone is one-third compared to a cylinder of the same parameters.
• The slant height of a cone is not its actual height.

Frustum of a Cone

When a cone, be it a regular cone or an oblique cone, is cut into half by a plane surface, the bottom half of the cone is known as the Frustum of the cone. The upper half of the sliced cone holds the shape of a cone, whereas the bottom half gets two circular faces with no edges.

This part of the cone is obtained when the cone is sliced parallel to the circular base. The volume and the surface area of the frustum of the cone cannot be calculated using the formulas of a regular cone.

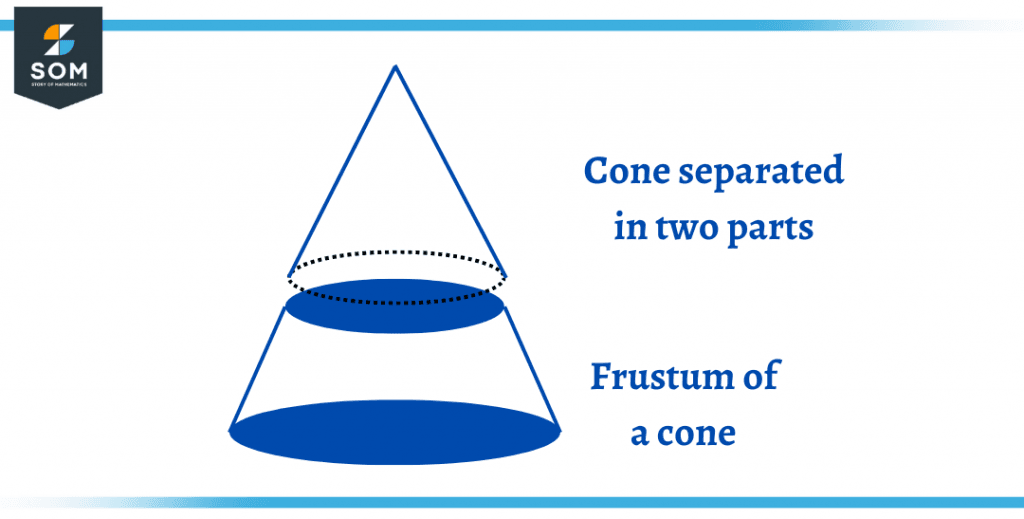
Figure 4 – A right cone sliced in half, forming the Frustum of cone

Solved Example

Find the slant height and volume of an oblique cone with r = 4cm, h = 7cm, and d = 2cm. Also, find the surface area of the base of the cone.

Solution

Using the formula of slant height:

Slant Height, l = $\sqrt{(2xr +d)^2 +h^2}$

Replacing the variables with there values gives us:

\[ l = \sqrt{(2(4) +2)^2 +7^2} \]

\[ l = \sqrt{(10)^2 +49} \]

The slant height of the oblique cone:

\[ l = \sqrt{149} = 12.2 \text{ cm} \]

Now using the formula for the volume of the oblique cone,

\[ V = \dfrac{1}{3} \times \pi r^2 \times h\]

Plugging in the values of radius, height, and pi:

\[ V = \dfrac{1}{3} \times 3.142 \times (4)^2 \times 7\]

\[ V = \dfrac{1}{3} \times 3.142 \times 16 \times 7\]

\[ V = 117.2 \text{ cm}^3 \]

Thus the volume of the cone comes out to be 117.2 $\text{cm}^3$.

All images/mathematical drawings were created with GeoGebra.

Oblique Definition < Glossary Index > Oblique Cylinder Definition