Operator|Definition & Meaning

Mathematical problems contain symbols known as operators, each of which stands for an operation that must be performed. They instruct us on the action that should be carried out. All mathematical operations and procedures are built on operators, which can be thought of as the fundamental building blocks. 

The operators reduce mathematics to the fundamentals that we make use of on a daily basis, regardless of whether or not we are aware of this fact. Following are the four fundamental operators used in mathematics.

• Addition
• Subtraction
• Multiplication
• Division

Figure 1: Four Fundamental Operators

Let’s examine each of these four fundamental operators, including their laws and some illustrations, in further detail.

Addition Operator (+)

The operator of addition is a mathematical operator that refers to the process of combining two or more quantities. The symbol for addition is a plus (+) sign, which indicates the operation of addition. The process entails integrating two or more numerical expressions into a single phrase.

When it comes to the addition operation, the order is irrelevant. This entails that the operation of adding is commutative in nature. It is possible for it to involve any kind of number, including real numbers, complex numbers, fractions, decimals, and so on.

Example of the Addition Operator

We can illustrate the addition operator through the following example

5 + 6 = 11

The summation of numbers is another name for the operation of adding more than two integers, values, or elements, and it can involve any number from one to n number of terms.

The Rules of Addition

Below is a list of the rules of addition that apply to integers.

• The result of adding two positive numbers together is also a positive
• The result of adding two negative numbers together is another negative
• When you are adding negative and positive integers, you should first minus the integers and then utilise the sign of the integer number with the highest value.

Subtraction Operator (-)

The difference among the two values can be determined by the use of the subtraction operator. The sign for subtraction is a minus sign, which looks like this (-).  It is nearly identical to addition; however, it is the inverse of the second element. The operator works in the opposite direction of addition.

The concept of subtraction refers to the process of adding the positive number to the negative number. The primary goal of this method is to determine how many items are still available after others have been eliminated.

Example of the Subtraction Operator

We can illustrate the Subtraction operator through the following example.

11 – 6 = 5

As discussed already, you can write the above expression in the following manner as well.

11 + (- 6) = 5

The Rules of Subtraction

Below is a list of the rules of subtraction that apply to integers.

• If the signs of both of the numbers are positive, then the result will be a positive
• The result of any subtraction operation will be a negative number if the signs of both of the numbers are negative.
• In the case where the signs of the numbers are not the same, minus the numbers, and then select the sign of the number that is greater among them.

Multiplication Operator (×)

The operation of multiplication is equivalent to adding the same number together repeatedly. It is indicated by the symbol “×.” In addition to this, it can combine with any number of values to produce a single value.

The terms multiplicand and multiplier are involved in the multiplication operation. The product is the term used to refer to the end result that is obtained by multiplying the multiplicand with the multiplier.

Example of the Multiplication Operator (×)

We can illustrate the multiplication operator through the following example.

3 × 4 = 12

In this case, the number “3” serves as the multiplier, whereas the number 4 serves as the multiplicand, while the result, “6,” is referred to as the product of the multiplication operation.

The outcome of multiplying two integers, denoted by ‘X’ and ‘Y,’ is a single value denoted by the term ‘XY,’ in which ‘X’ and ‘Y’ are the factors of the resulting final value.

The Rules of Multiplication

Below is a list of the rules of multiplication that apply to integers.

The rules for multiplying numbers are presented in the following paragraphs.

• A positive result is obtained when two positive numbers are multiplied together.
• A positive result is obtained when two negative numbers are multiplied together.
• A negative result is obtained when a positive and a negative number are multiplied together.

Division Operator (÷)

The operation of division, which is the opposite of multiplication, is typically represented by the symbol “÷.”  It is composed of the two words dividend and divisor, with the dividend being the component that is divided by the divisor to produce the singular term value.

In case the dividend is higher than the divisor, then the quotient that is obtained is larger than 1, whereas if the divisor were higher, the quotient that is obtained is lower than 1.

Example of the Division Operator (÷)

We can illustrate the division operator through the following example.

10 ÷ 5 = 2

In the above equation, “10” represents the dividend, “5” represents the divisor, and the outcome, “2,” is referred to as the quotient.

The Rules of Division

Below is a list of the rules of division that apply to integers.

• The result of dividing a positive number by another positive number is also a positive
• If you divide two negative numbers together, you will get a positive number
• If you divide integers that have opposite signs from each other, you will get a negative

Significance of Operators

The use of operators, such as addition (+), Subtraction (-), multiplication (×), and division (÷), is a necessary component in the development of more complicated mathematical calculations and algorithms. They are utilized in a wide variety of disciplines, including the realms of economics, engineering, and computer science, to carry out fundamental calculations.

In addition, they are utilized in activities that are part of everyday living, such as determining how much of a tip to leave at a hotel or balancing a checkbook. For more sophisticated mathematical and computational tasks, it is vital to have a solid understanding of and facility with these fundamental operators.

Example

Solve the following statements using mathematical operators.

1. James purchased 5 more apples after having 6 already. How many apples does James have now?
2. Of the total apples James had, he gave 3 to john. How many apples are left with James?

Solution

According to the data given in statement (a):

Total apples James has = 6 + 5

Total apples James has = 11

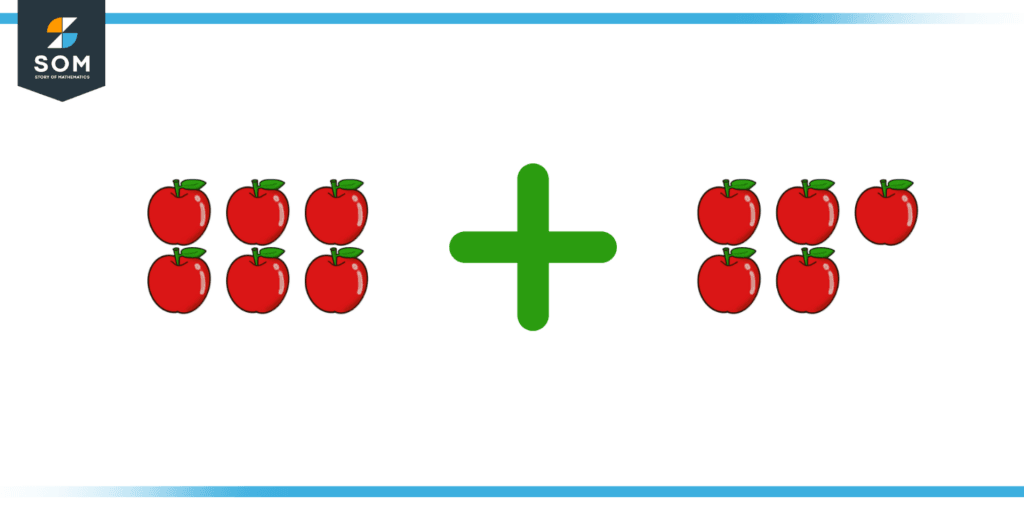
Figure 2: Illustration of Addition Operation

Now, as mentioned in statement (b), James gave 3 apples to John. Thus:

Total apples left with James = 11 – 3

Total apples left with James = 8

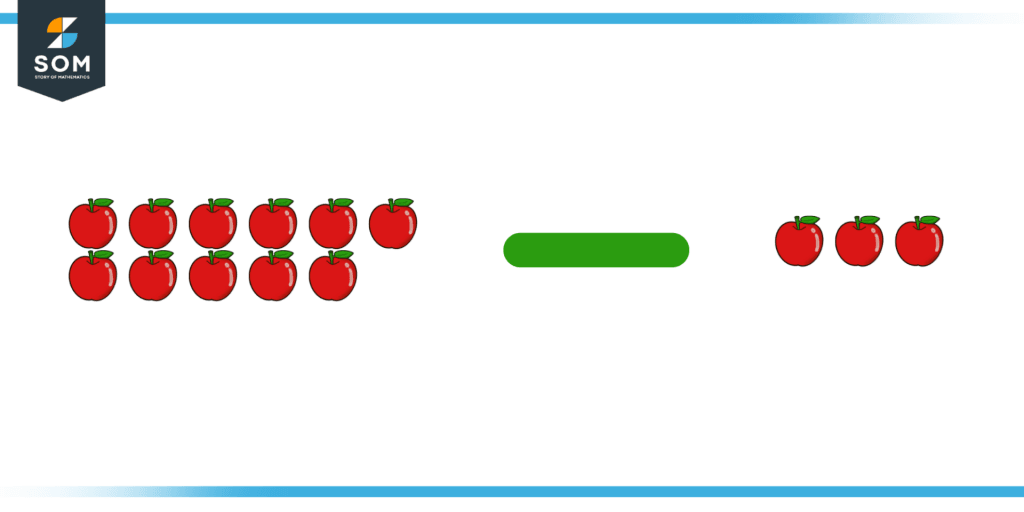
Figure 3: Illustration of Subtraction Operation

All images/mathematical drawings were created with GeoGebra.

Operation Definition < Glossary Index > Opposite Numbers Definition