JUMP TO TOPIC
Opposite Numbers|Definition & Meaning
Definition
A number and its negative counterpart are called opposite numbers. Adding two opposite numbers results in a zero. If you plot opposite numbers on the number line, they appear in exactly opposite positions and are the same distance away from zero on either side.
Figure 1 below shows the opposite number of 3.
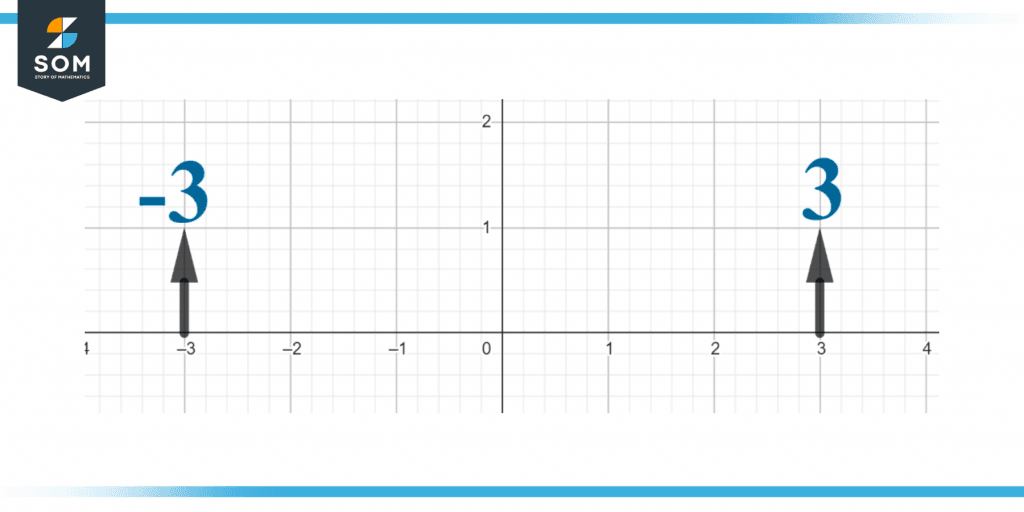
Figure 1 – Representation of opposite numbers.
What are Opposite Numbers?
When the sum of two integers equals zero, the value is known as the opposite number. If x+y=0, m is known as the inverse number of n. Take notice of the fact that m=-n.
In some circumstances, opposing integers are known as additive inverses.
According to the definition, -x is the inverse (or additive inverse) of x and vice versa. Because 1+(-1)=0, one may conclude that -1 is the opposite of 1. In the same way, 1 is regarded as the inverse basically of the number -1. The inverse of a number is the value on the opposite end of the 0 line segment and in the same place as 0.
A quantity’s additive inverse is its inverse. The number product itself with its inverse is zero. (This feature is also termed the opposites feature).
Opposite Number Properties
- The product of a number with its inverse is zero.
- Numbers and their inverses have the same range from 0 but are on the line segment in the other direction.
- A negative number is the inverse of a positive number. Similarly, a positive number is the inverse of a negative number.
- The absolute value of a number and its inverse is the same. For instance, -2 is the inverse of 2. It is worth noting that 2 and -2 are the same absolute value. 2 as |2|=|-2|=2
Definition of opposite integers
Assume n is an integer. The number -n is thus known as the inverse integer of n since the sum n+(-n)=0. For instance, -20 is the inverse number of 20.
According to the concept of opposite integers, the inverse of the positive integer is indeed a negative integer, and the inverse of just a negative integer would be a positive integer.
For example, the opposite integer for 10 is -10, and the opposing integer for -10 is 10 since 10 + (-10) = 0.
Opposite Numbers as Additive Inverse
An additive inverse is a number added to a given amount to make the total zero. For instance, the outcome is zero when we take the integer 3 and multiply it by -3. As a result, the additive inverse for 3 is -3. In everyday life, we encounter circumstances in which we nullify the value of a number by calculating its additive inverse.
Figure 2 below shows the additive inverse of a number.

Figure 2 – Representation of additive inverse.
A number’s additive inverse is its inverse number. When a number is multiplied by its additive inverse, then the sum of both numbers equals zero. The straightforward approach is to convert a positive number to something like a negative value and vice versa. We already know that 1+ (-1) Equals 0. As a result, -1 has been the additive inverse for 1, while 1 is the additive inverse for -1.
Inverse Additive Property
Once the sum of two actual figures is zero, each is described as an additive inverse of the other. As a result, R + (-R) equals 0, whereby R is a positive integer. R and -R are additive inverses of one another.
For instance, (1/2) + (-1/2) equals 0. In this case, 1/2 is an additive inverse for -1/2 and vice versa. That’s an example of a fraction’s additive inverse.
Assume you have a pail of room-temperature water. You pour in a liter of hot water, raising the total temperature of something like the bucket by a given amount. Pour in another liter of cold water. The different water temperatures in a bucket will balance each other out, resulting in a bucket of room-temperature water.
The same approach applies to determining a number’s additive inverse. The additive inverse feature applies to both real and complex numbers.
Inverse Additive of Real Numbers
A natural value, a decimal, a whole number, a fraction, an integer, or any real number can be specified. The negative of a given integer is the real number’s additive inverse.
Inverse Additive Formula
The generic equation again for the additive inverse of the number can be written in the number’s form. When any number is added to its inverse, it cancels out, and the total sum is zero. We must find the inverse of the provided integer X. In many other words, we must discover -1 * X. As a result, we may say:
Additive Inverse of X = -1(X)
Figure 3 below shows the formula for the additive inverse.

Figure 3 – Additive inverse formula.
Multiplicative Inverse and Additive Inverse
Numbers have two properties: multiplicative inverse and additive inverse, which are connected to multiplication and addition operations. For a number x, the additive inverse is – x, while the multiplicative inverse is 1/x.
Additive inverse of x2 + 1 is -x2 – 1.
Examples of Opposite Numbers
Here are some examples of opposite numbers.
Example 1
What’s the additive inverse expression of 12x + 4y – 8z?
Solution
We must determine an additive inverse of an entire equation to obtain the solution.
It may be found simply multiplying the entire equation by -1.
12x + 4y – 8z
Multiplying it by -1, we get:
-1(12x + 4y – 8z) = -12x – 4y + 8z
Answer: -12x – 4y + 8z is an additive inverse for the given expression.
Example 2
Subtraction of the given inverse number: Subtraction of -6 from 6.
Solution
When we have to subtract the opposite number, that is, a negative number from the positive number, we will use the subtraction rule, ‘Alter the action from subtraction towards addition, and switch the sign of either the second number which follows.’
In this situation, subtracting -6 – (6):
= -6 – 6 = -12,
Hence, the answer is -12.
All Images are made using GeoGebra.
