JUMP TO TOPIC
Opposite Side|Definition & Meaning
Definition
A triangle’s opposite side is the side that lies opposite to the angle of interest and is not one of the sides that make the angle. An opposite side is always associated with reference to an angle. Without the angle reference, it is just a side of a triangle.
Figure 1 shows the opposite side PR to the angle s in a triangle PQR.
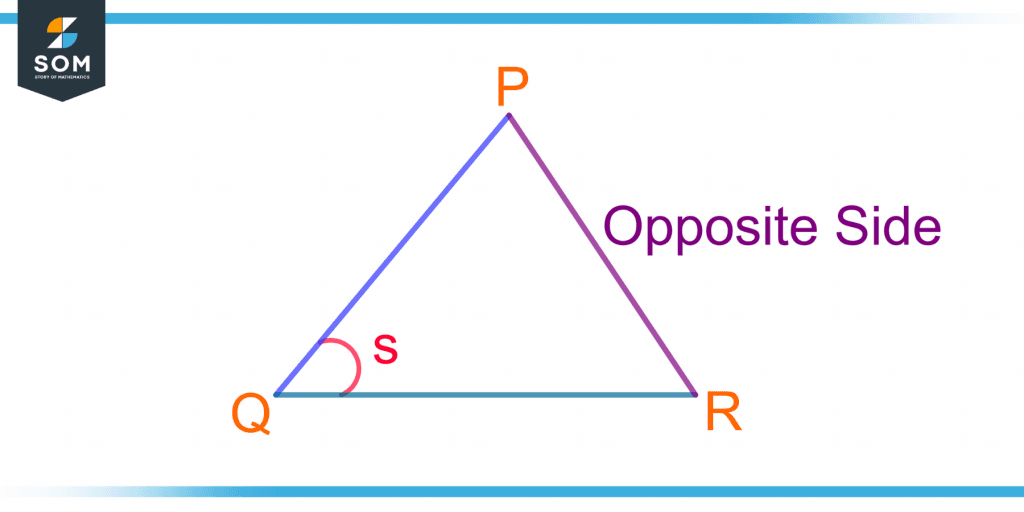
Figure 1 – Illustration of an Opposite Side PR to an Angle s in a Triangle PQR
Right-angle Triangle
A right-angle triangle is characterized by a right(90°) angle. Its two sides are perpendicular to each other. Trigonometry is based on the relationship between the angles and sides of a right-angle triangle.
A right-angle triangle consists of a hypotenuse which is the opposite side to the right angle and is the longest side. In this case, the angle of interest is the 90° angle.
In contrast to the opposite side, the adjacent side makes the angle of interest. If an angle theta(θ) is formed between the hypotenuse and the adjacent side, then the perpendicular side will be opposite to θ.
Sometimes, the adjacent side is referred to as the base, and the opposite side is the perpendicular in the right-angle triangle.
Figure 2 shows a right-angle triangle ABC with AC as the hypotenuse, the adjacent side as BC, and the opposite side as AB with reference to angle θ.
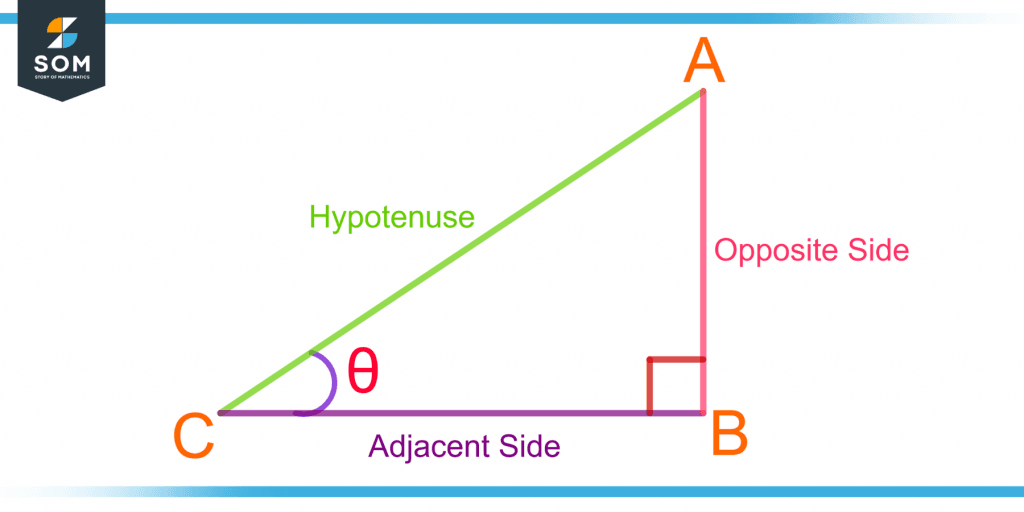
Figure 2 – Demonstration of Opposite Side, Adjacent Side, and Hypotenuse in a Right-Angle Triangle
Pythagoras Theorem
The Pythagoras theorem is only for right-angle triangles. It states that hypotenuse square is equal to the sum of the square of the base b(adjacent side) length and the perpendicular p(opposite side) length.
Mathematically, it is:
h2 = p2 + $b2
Figure 3 shows the right-angle triangle with hypotenuse h, perpendicular p, and the base b.
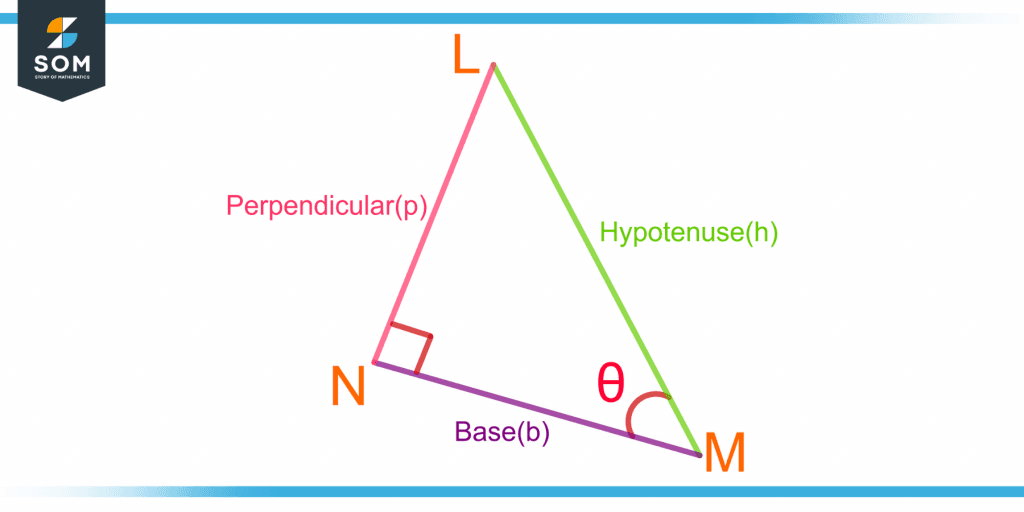
Figure 3 – Demonstration of Base, Perpendicular and Hypotenuse in a Right-Angle Triangle
Where LN is the opposite side, and MN is the adjacent side of angle θ.
Trigonometric Functions
Trigonometric functions are the relationship between an angle and the ratio of two side lengths of a right-angle triangle. These are sine, cosine, and tangent, which are mostly used. The notation for sine is “sin,” cosine is “cos,” and for tangent is “tan.”
Consider figure 2 for the trigonometric ratios. If the length of the side “a” is opposite to angle θ, b is the adjacent side, and c is the hypotenuse, then:
sin θ = opposite / hypotenuse = a / c
cos θ = adjacent / hypotenuse = b / c
tan θ = opposite / adjacent = a / b
The angle θ should be acute i.e. between 0° and 90°. These ratios suggest that the ratio of any two sides of the triangle depends on the angle θ.
The three ratios are related as follows:
tan θ = sin θ / cos θ
The three angles of a triangle add up to 180°. Hence, a right-angle triangle has two acute angles that sum up to 90°.
Less Common Trigonometric Functions
The reciprocals of the above trigonometric functions are the less-used functions. These are cosecant, secant, and cotangent. The notations for cosecant, secant, and cotangent are cosec or csc, sec, and cot, respectively. These ratios are given as follows:
cosec θ = 1 / sin θ = hypotenuse / opposite = c / a
sec θ = 1 / cos θ = hypotenuse / adjacent = c / b
cot θ = 1 / tan θ = adjacent / opposite = b / a
Semi-perimeter
Semi-perimeter is defined as half of the perimeter of a polygon. The following formula gives the semi-perimeter s of the three sides a, b, and c of the triangle as follows:
s = (a + b + c) / 2
If a is the opposite side, b is the adjacent side and c is the hypotenuse of a right-angle triangle, then the equation for the semi-perimeter is given as:
(s – a)(s – b) = s(s – c)
Law of Cosine
The law of cosine deals with the opposite side of the triangle. It states that the square of a side opposite to an angle is equal to the sum of the square of the remaining two sides that make the angle minus two times the product of the remaining sides and the cosine of that angle.
Consider A, B, and C as three angles of a triangle, as shown in figure 4. Let the sides b, c, and a be opposite to the respective angles B, C, and A.
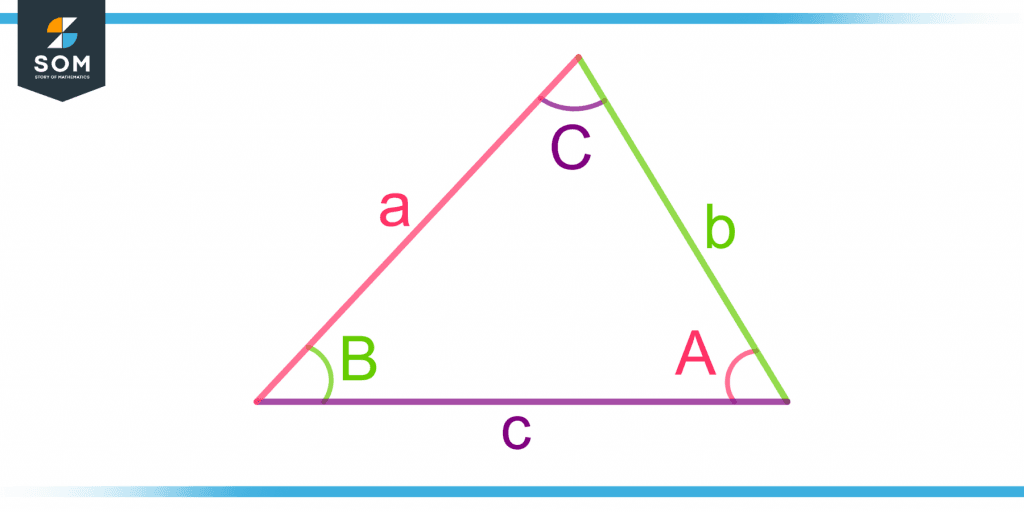
Figure 4 – Demonstration of Sides Opposite to Angles in a Triangle for the Law of Cosine
The three equations for the law of cosine are given as follows:
b2 = c2 + a2 – 2ca.cos(B)
c2 = b2 + a2 – 2ba.cos(C)
a2 = c2 + b2 – 2cb.cos(A)
The law of cosine is helpful in finding the third side of a triangle when its opposite angle and the sides enclosing it are known. It can also be used to find the angle opposite to a side if the three sides are known.
The cosine rule generalizes the Pythagoras theorem, which is only for right angles. If angle A = 90°, then cos A = 0, hence the first equation for the cosine rule becomes:
a2 = b2 + c2
which is the Pythagoras theorem.
Examples
Example 1 – Identifying Opposite Sides
Three triangles are shown in figure 5. In each triangle, identify the opposite side and the adjacent side to the angle θ. Which of the three triangles is a right-angle triangle? Also, identify the hypotenuse and the right angle in the right-angle triangle.
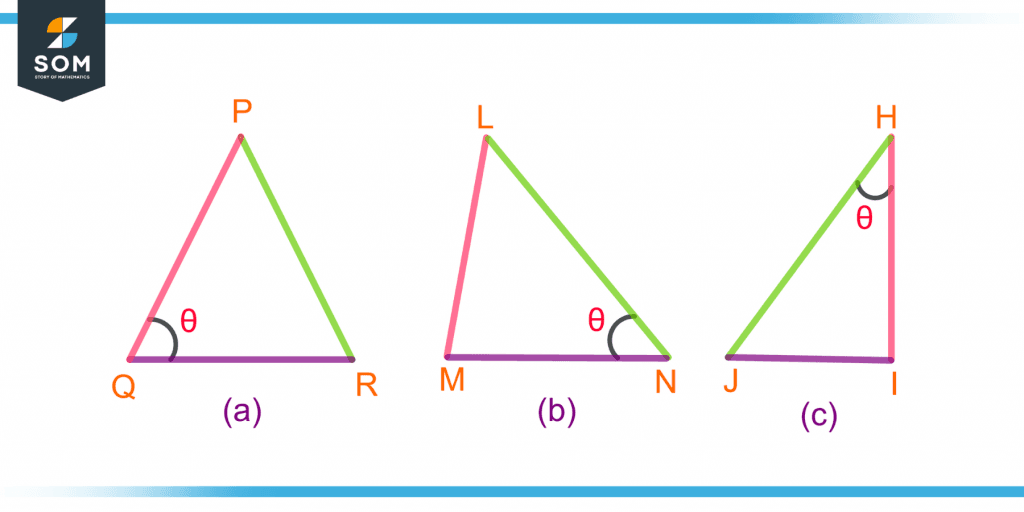
Figure 5 – Identifying the Opposite and Adjacent Sides in the Three Triangles
Solution
In triangle (a) PQR, the opposite side to angle θ is PR, and the two adjacent sides to angle θ are PQ and QR, which constitutes the angle.
In triangle (b) LMN, the opposite side to angle θ is LM, and the adjacent sides are LN and MN.
The third triangle (c) HIJ is a right-angle triangle with a 90° angle HIJ. The side opposite to angle θ is JI, and the adjacent side is IH. The hypotenuse is HJ, as it is the longest side.
Example 2 – Calculating the Length of the Opposite Side Using the Trigonometric Functions
A triangle MNO is given in figure 6. Calculate the length of the side opposite to angle θ. The hypotenuse is given as 4.9 cm.
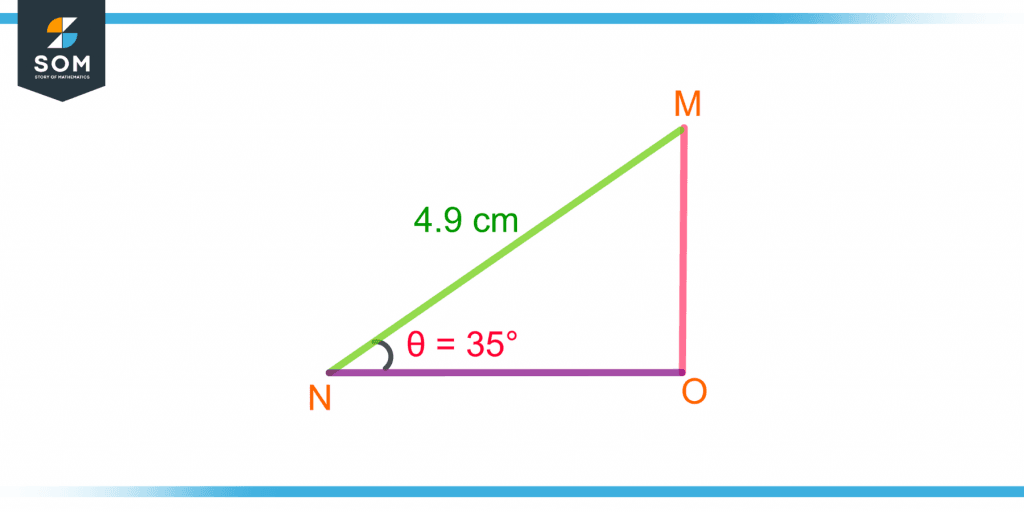
Figure 6 – Calculating the Opposite Side Using a Trigonometric Function
Solution
The opposite side to angle θ is OM. Using the function:
sin θ = opposite / hypotenuse
This equation can be written as:
Opposite = (sin θ)(hypotenuse)
Here, θ = 35° and hypotenuse = 4.9 cm, putting the values in the above equation gives:
Opposite = (sin 35°)(4.9)
Opposite = (0.57)(4.9)
Opposite = 2.8 cm
So, the opposite side OM is equal to 2.8 cm.
Example 3 – Calculating the Opposite Side Length Using the Law of Cosine
Figure 7 shows a triangle. Calculate the side opposite to angle A.
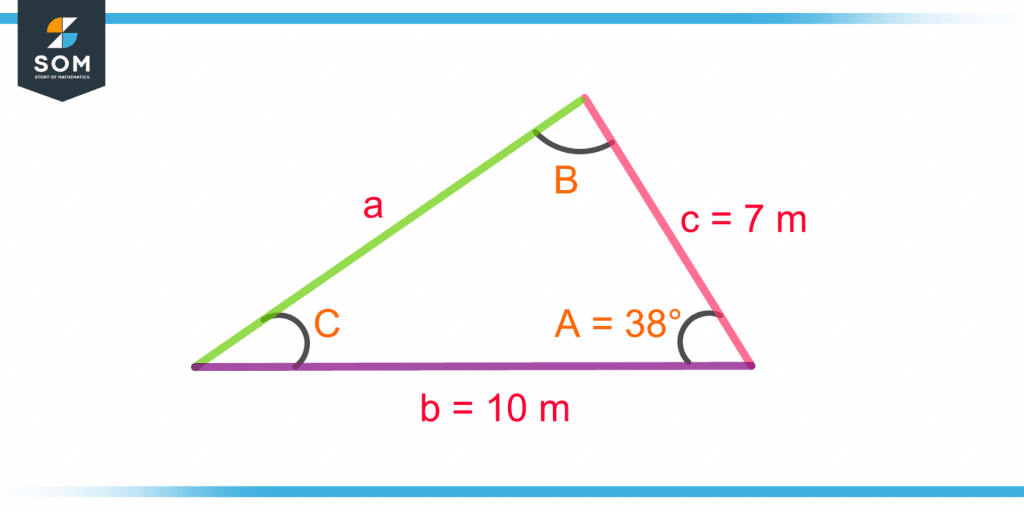
Figure 7 – Calculating the Opposite Side Using Law of Cosine
Solution
The opposite side “a” to angle A can be calculated using the cosine rule:
a2 = c2 + b2 – 2cb.cos(A)
Where:
b = 10 m, c = 7 m, angle A = 38°
Putting the values in the above equation gives:
a2 = (7)2 + (10)2 – 2(7)(10)cos(38°)
a2 = 49 + 100 – 140(0.788)
a2 = 149 – 110.32
a2 = 38.68
Taking square root on both sides gives:
a = 6.22 m
So, the side opposite to angle A is equal to 6.22 m.
All the images are created using GeoGebra.
