JUMP TO TOPIC
Order of Operations|Definition & Meaning
Definition
A prescribed sequence of rules that one must follow when solving any given mathematical expression is called the order of operations.
In solving any arithmetic problem involving different sets of equations or arithmetic expressions involving addition, subtraction, multiplication, and division, we need to follow some rules to decide which operation to evaluate first, as different orders produce different results.
Building the Concept
Suppose a mathematical expression involves various arithmetic operations like addition, subtraction, division, and multiplication, along with expressions like exponents and brackets. How would you try to solve the problem?
If we try to randomly evaluate the expression by opting random order of arithmetic operations, we can end up getting the wrong result.
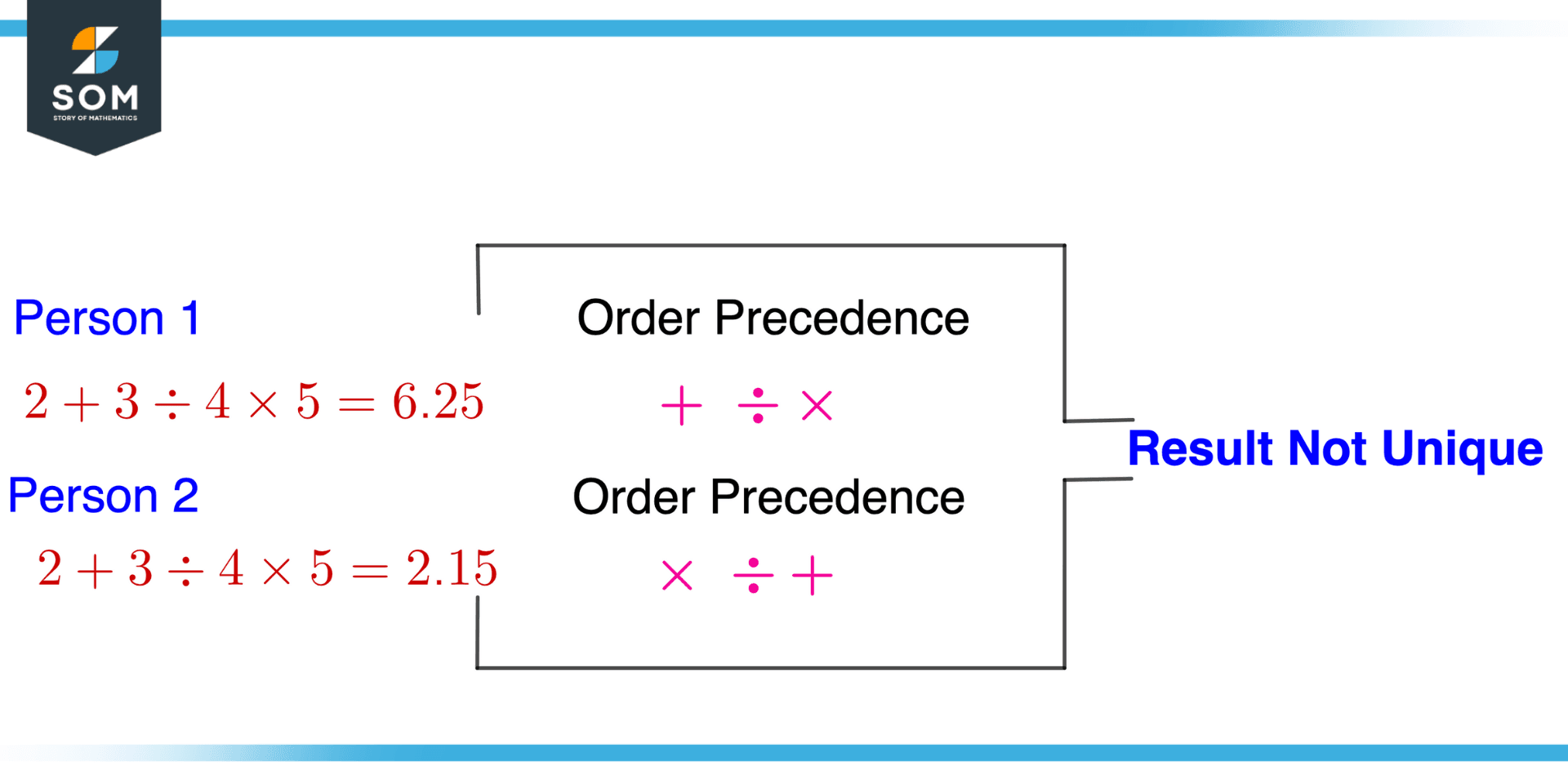Figure 1 – Concept Illustration of Order of Operations
Let us take an example. Person 1 tries to solve the mathematical expression by prioritizing addition over division and multiplication, and person 2 tries to solve the same expression by prioritizing multiplication over division and addition. As shown in Figure 1, the result of both persons will end up giving different results, which does not make any sense.
This is why the order of operations is important. It specifies a standard operating procedure for solving a mathematical expression in a specific order to ensure the same result for the same mathematical problem. We have made the convention in which each arithmetic operation is evaluated with respect to its priority or order.
Two Order of Operations Conventions
There are generally two conventions of the order of operations for solving mathematical expressions. The first is known as PEMDAS, and the second is known as DMAS.
PEMDAS
Figure 2 – PEMDAS Convention
PEMDAS is an acronym used for the order of arithmetic operations on mathematical operations. P is used for Parenthesis, E is used for exponents, and M is used for multiplication, D is used for division, A is used for addition, S is used for subtraction.
First Precedence
Parenthesis {}, [], ()
If a mathematical expression involves any of the above brackets, then the expression inside this bracket will be evaluated first.
Second Precedence
Exponents, Let x be any number and y be any power. Then $x^{y}$ is the exponent. If the mathematical expression contains any term related to this representation, it would be evaluated on the second number after evaluating the first order that brackets.
Third Precedence
If the mathematical expression contains a multiply sign, we evaluate it after evaluating brackets and exponents.
Fourth Precedence
If a mathematical expression constitutes any division operation, it is performed after dealing with brackets, exponents, and multiplication.
Fifth Precedence
Suppose there is a mathematical expression with brackets, exponent, division, multiplication, and addition operations; the addition operation will be treated lastly precedence-wise or at fifth precedence.
Sixth Precedence
Suppose there is a mathematical expression with brackets, exponent, division, multiplication, addition, and subtraction. Then the precedence for using subtraction operation will be at sixth or last.
DMAS
Figure 3 – DMAS Convention
This is another convention used for precedence or order of using arithmetic operations. This convention is applied to a mathematical expression that contains only four arithmetic operations namely addition, subtraction, division, and multiplication. The precedence is described above.
First Precedence
Suppose there is a mathematical expression involving only division and multiplication. Then, the first precedence will be given to the division operation.
Second Precedence
Multiplication has the second precedence when treating such problems. If there is an expression involving multiplication and subtraction only, then multiplication must be performed first.
Third Precedence
The addition has the third precedence while solving such kinds of problems, but if there is only an addition and subtraction operation in the expression, then addition will have the first precedence.
Fourth Precedence
While solving such problems described above, we give the least precedence to subtraction which is fourth. In any convention, whether PEMDAS or DMAS, subtraction precedence will be last in any case.
General SOPs for Order Precedence
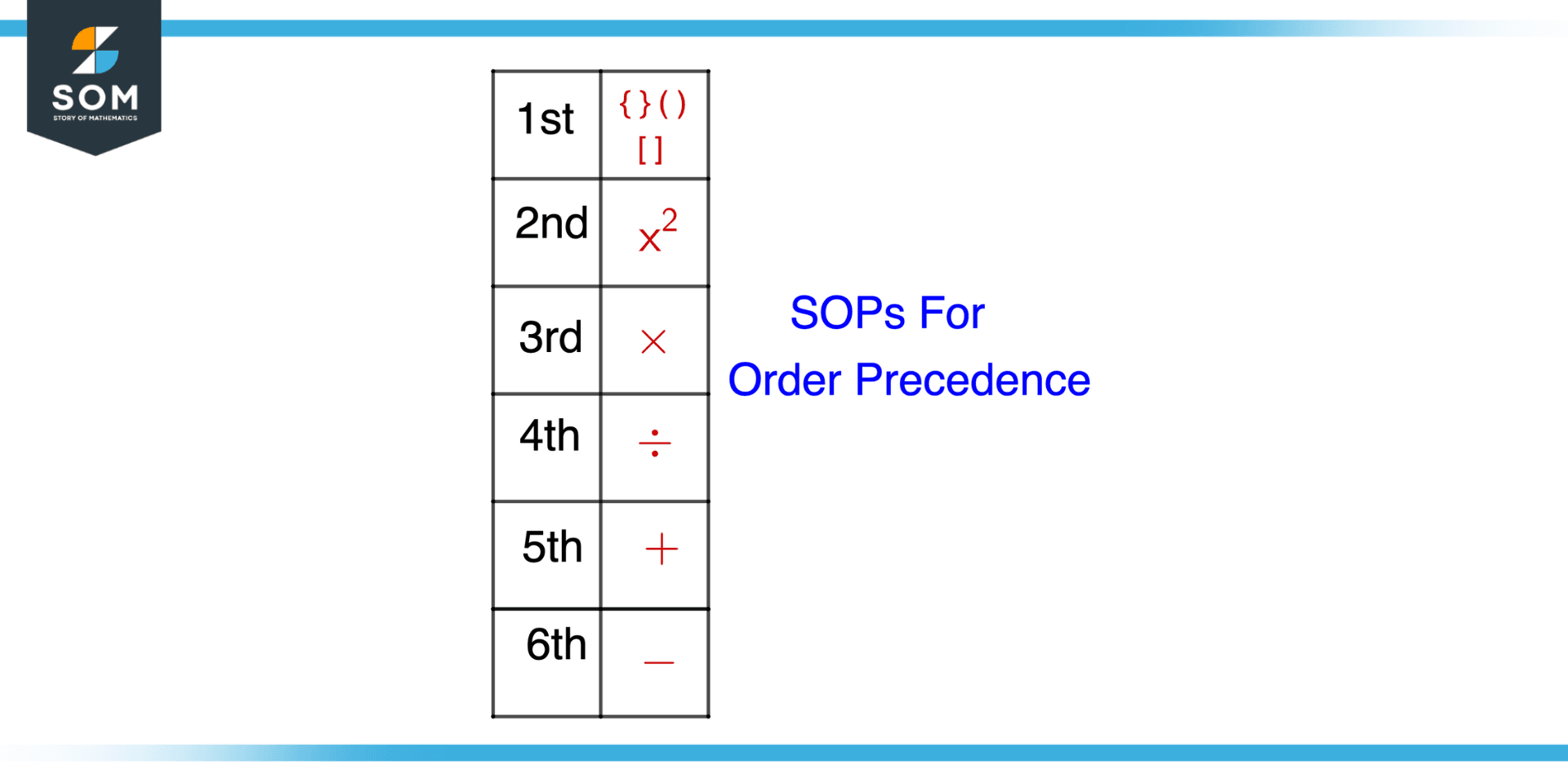
Figure 4 – Sops for Order Precedence for Arithmetic Operations
SOP 1
Always solve brackets first in any mathematical expression. There are different types of brackets: round “(),” curly “{},” and square “[].” () are solved first, followed by {}, followed by [].
SOP 2
Always give the second precedence to the exponents. For example, if this is the expression (2+3) x 5$\mathsf{^2}$, then always solve the exponent secondly.
SOP 3
Talking about arithmetic operations left behind Multiplication, Addition, Division, and Subtraction. Then, we will use multiplication or division on the third precedence after brackets and exponents.
SOP 4
After solving brackets, exponents, multiplication, and division, we solve addition and subtraction at the end, respectively.
Riddles To Memorize the Order of Operations
- PEMDAS: Party Every Month Dance Always Sunday
- DMAS: Dance Madly After Sunday
Example Problems Involving Multiple Operations
Example 1
a = [(5 + 10) + 4$\mathsf{^2}$ x 4 – 42 + 50] $\div$ 10
Solve the above example using the PEMDAS convention for order precedence.
Solution
First Precedence: Solve all expressions within round brackets (). This is 5 + 10 = 15.
Second Precedence: Solve all expressions within the square brackets. This is 15 + 4$\mathsf{^2}$ x 4 – 42 + 50.
Third Precedence: Solve exponent 4$\mathsf{^2}$ = 16.
Fourth Precedence: Multiply 16 by 4 to get 64.
Fifth Precedence: Add 15, 64, and 50 to get 129, then subtract 42 to get 87. This is the result of the expression within [].
Last Precedence: Solve expression outside the bracket. This is a division by 10, so we will divide 87 with 10 to get 8.7.
Following the PEMDAS order of operations:
a = [(5 + 10) + 4$\mathsf{^2}$ x 4 – 42 + 50] $\div$ 10
a = [(15) + 4$\mathsf{^2}$ x 4 – 42 + 50] $\div$ 10
a = [15 + 16 x 4 – 42 + 50] $\div$ 10
a = [15 + 64 – 42 + 50] $\div$ 10
a = [129 – 42] $\div$ 10
a = [87] $\div$ 10
a = 8.7
Example 2
Solve the following mathematical expressions using DMAS.
a = 28 $\div$ 4 – 15 x 20 + 30
b = 40 – 30 + 12 x 4 + 5 $\div$ 3
Solution
Expression A
First Precedence: Divide 28 by 4.
Second Precedence: Multiply 15 by 20.
Third Precedence: Add 30 with the result of a division of 28 by 4.
Fourth Precedence: Subtract 300 from the final result.
Following this order of operations:
a = 28 $\div$ 4 – 15 x 20 + 30
a = 7 – 15 x 20 + 30
a = 7 – 300 + 30
a = -300 + 37
a = -263
Expression B
First Precedence: Divide 5 by 3.
Second Precedence: Multiply 12 by 4.
Third Precedence: Add 40 with the result of a division of 5 by 4 and multiplication of 12 by 4.
Fourth Precedence: Subtract 30 from the final result.
Following this order of operations, we get the following result:
b = 40 – 30 + 12 x 4 + 5 $\div$ 3
b = 40 – 30 + 12 x 4 + 1.666
b = 40 – 30 + 48 + 1.666
b = 89.666 – 30
b = 59.666
All mathematical drawings and images were created with GeoGebra.