Ordinal Number|Definition & Meaning

What Are Ordinal Numbers? 

Ordinal numbers show the location or order of anything to other numbers, such as first, second, third, and so on. An ordinal number is a number that represents the placement or order of something. This order or series could be determined by factors such as size, significance, or any chronology.

First, look at an example to better comprehend the ordinal numbers. The competition had ten participants from the school. The top three winners were recognized as coming in first, second, and third place, respectively, and were awarded medals. Ordinal numbers represent the places of first, second, and third, respectively, in this scenario.

Figure 1: Representation of ordinal numbers

How Should Ordinal Numbers Be Written?

An additional digit, or suffix, is tacked on to the end of the ordinal numbers. In words, they can be represented as first, second, third, and so forth in sequential order. When expressing ordinal numbers as numerals, the last two letters of the corresponding nouns are appended to the respective components, such as “first,” “second,” “third,” “fourth,” and so on.

Why Do We Utilize Ordinal Numbers?

Ordinal numbers are used whenever we need to define the position of something or the order in which something occurs. As an illustration, the pens are stored in the fourth drawer from the bottom, and Ria occupies the second level of the apartment.

In this instance, the relevant numbers designate the location or sequence in which the object or persons are presented, depending on the context.

Differences Between Cardinal Numbers and Ordinal Numbers

A number that represents the count of something is referred to as a cardinal number. A cardinal number is a natural number such as 1, 2, 3, etc., while an ordinal number specifies an object’s position or place. Cardinal numbers include any natural number such as 1, 2, 3, etc.

For instance, first, second, third, fourth, fifth, etc. Consider the following scenario: “There are six cats and seven parrots.” The preceding is an illustration of a cardinal number. Ordinal numbers are represented when we say, “The rank of the participants in the marathon race is first, second, third, and so on.”

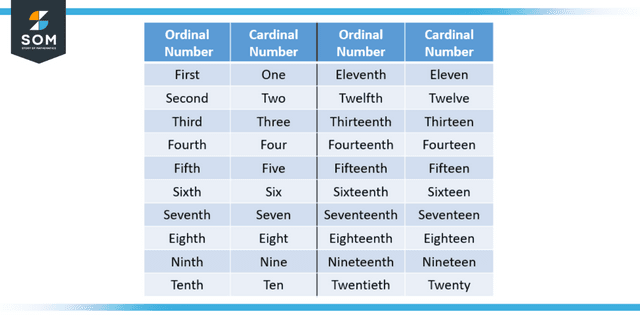
Figure 2: Difference between ordinal and cardinal numbers

Ordinal Numbers 1 to 20

The ordinal numbers range from 1 to 20 and are distinct from the other numbers. One can see a pattern of repeating ordinal numbers just after the number 20, starting with the number 21. The following is a list of the ordinal numbers from 1 to 20 in ascending order. One is the first, 2 is the second, 3 is the third, and so on.

The fourth represents the fourth place, the fifth, the sixth, the seventh, eighth the eighth, nine the ninth, ten the tenth, eleven the eleventh, twelve the twelfth, thirteen the thirteenth, fourteen the fourteenth, fifteen the fifteenth, sixteen the sixteenth, seventeen the seventeenth, eighteen the eighteenth, nineteen the nineteenth, and twenty the twentieth.

Various Applications of the Ordinal Number System

Ordinal numbers are a fantastic tool for elucidating the hierarchy of any given subject. Take, for instance, the sequence of the dates. These numerals are only used when there is data to be put in order and data to be arranged.

For instance, someone who has maintained a high level of performance all year may be offered the opportunity to serve as valedictorian. They would be at the front of the line.

However, someone who did well academically but could not achieve as highly as the person who came before them in various tests and exams can be in the running for the position of valedictorian. The individual who has not scored particularly well at any point has the slimmest chance of winning.

Difference Between Ordinal and Nominal Numbers

The term “nominal numbers” refers to a group of numbers written on labels attached to specific things or locations to make them more easily identifiable. When we need to identify anything uniquely, we utilize nominal numbers.

These statistics won’t tell you anything about the quantity, quality, or anything else associated with the subject; they will only offer you information on its location.

There are a variety of applications for nominal numbers, including use as area codes and on the license plates of cars. Mathematical operations such as adding, subtraction, multiplication, and division are nonsensical when dealing with nominal numbers.

For illustration purposes, 202 588-6500 is an example of a notional number. Even if we operate on the data, we will get insignificant results.

Figure 3: Descending order of ordinal numbers

On the other hand, ordinal numbers give us information about the position or rank of anything or person they are assigned to.

Take David, for instance; she is a resident of the 34th house on San Fransisco Avenue in Florida.

Is 0 an Ordinal Number?

No, the number 0 cannot be included in the category of ordinal numbers. It is impossible to provide a logical explanation by referring to the placement of anything as “zeroth” or “zeroth.”

Example 1

Anna, Jimmy, Carla, Peter, David, and Gorge are sitting in a row in alphabetical order. What are the positions of Jimmy and Peter starting from the beginning?

Solution

According to the alphabetical order, “A” comes first, so 1^st position is occupied by Anna, 2^nd position is occupied by Carla, 3^rd is occupied by David, 4^th is occupied by Gorge, 5^th is occupied by Jimmy, and the 6^th position is occupied by Peter.

So, Jimmy and Peter occupy the 5^th and 6^th positions, respectively.

Example 2

In words, “unfortunately,” “proud,” and “generosity,” what is the position of the letter “o” in all of them?

Solution

The position of “o” in “unfortunately” is 4^th.

The position of “o” in “proud” is 3^rd.

The position of “o” in “generosity” is 6^th.

All images/graphs are created using GeoGebra.

Order Of Operations Definition < Glossary Index > Origin Definition