JUMP TO TOPIC
Origin|Definition & Meaning
Definition
The intersection of the coordinate axes can be called as the origin in mathematics. The coordinates’ zero point is where it is.
Origin is referred to as the first point or the starting point from which we begin our calculations or measurements in mathematics, particularly in the area of coordinate geometry.
The 0 on a ruler is the point at which we begin taking measurements; as such, it is referred regarded as the scale’s origin. We weigh ourselves when the scale reads zero on a scale.
When it comes to temperature, it gets colder below zero degrees Celcius and hotter than zero. As a result, it serves as the starting point for our measurements.
Number Line Origin
The number zero is known as the origin on the number line. It divides the number line into two sections, as seen below:

Figure 1 – Origin On The Number Line
The negative numbers are on the left side of the origin, and the positive numbers are on the right. We always refer to the origin, or zero, when we claim that we have started from a particular position. The origin, or 0, is greater than the negative numbers and smaller than the positive numbers.
Origin in Two Dimensions
Two axes can be found in a flat coordinate plane; one is the y-axis, which is vertical, and the other is the x-axis, which is horizontal. These two axes meet at the origin. This origin point is commonly referred to as O and has the coordinates (0,0).
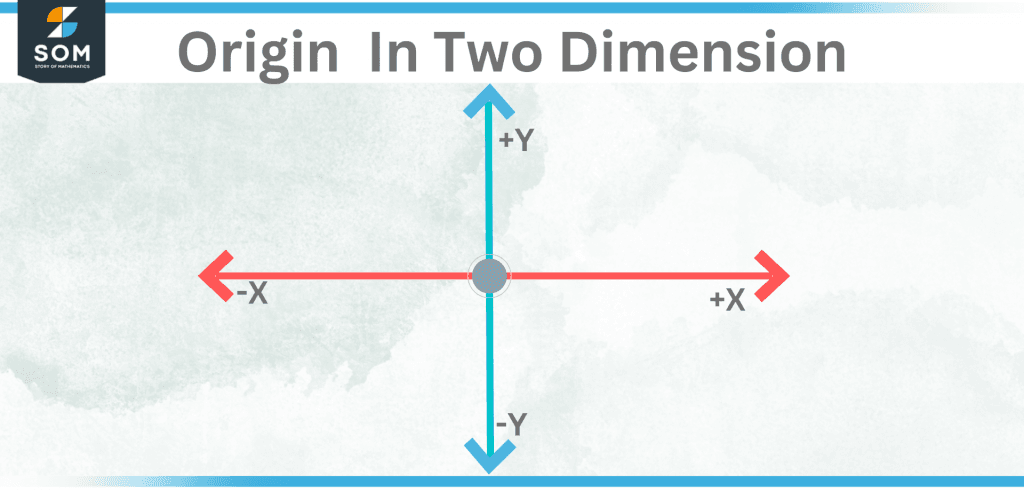
Figure 2 – Origin In Two Dimensions
Origin in Three Dimensions
The z-axis is a third axis that is present in a three-dimensional (3D) coordinate system in addition to the x-axis and y-axis. This z-axis can be thought of as entering and exiting the screen at an angle of right angles to the other two axes (x-axis and y-axis).
All three axes intersect at the origin, which is once more designated as point O. There are coordinates for this point (0,0,0).
The Cartesian Plane Origin
Vertical and horizontal number lines combine to form the Cartesian Plane. The intersection point commonly referred to as the origin, is where these two number lines cross. It is represented by the letter O, which serves as a fixed point of reference for the surrounding plane’s geometry.
The symbols for the origin’s coordinates are (0, 0). It denotes that x and y are both zero at the origin. Each of these axes is split in half by the origin into a positive and a negative half.
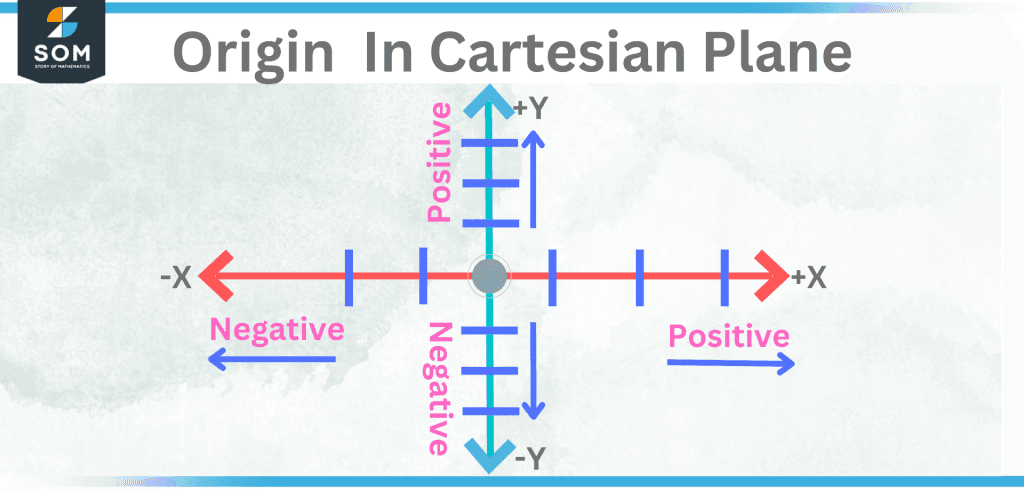
Figure 3 – Origin In Cartesian Plane
The Point’s Distance From the Origin
1. The Point Is on the X-axis
Any point on the x-axis has the form (x, 0). Its separation from the origin will only be x units.
Think about the following two points: A(4, 0) and B. (–4, 0). Let’s now determine how far they are from the starting point.
A(4, 0)’s separation from the origin is equal to |4| units, or 4 units.
B(-4, 0) is 4 units away from the origin at a distance of |-4| units.
This indicates that both locations are located 4 units apart from the origin.
Because distance cannot be negative, the absolute value sign must be used.
2. Point Is Located on the Y-axis
Any point on the y-axis has the form (0, y). Its separation from the origin will only be y units.
Any point on the y-axis has the form (0, y). Its separation from the origin will only be y units.
Take into consideration P(0, 4) and Q, two points (0, –4). Let’s now determine how far they are from the starting point.
P(0, 4) is located 4 units away from the origin at a distance of |4| units.
Q(0, -4) is four units away from the origin at a distance of |-4| units.
Therefore, these points are equally spaced apart from the origin.
Equation of a Line Through the Origin
The lines that go through the origin have the formula y = mx, where m is a constant. In this case, “m” can be either rational or irrational.
Take y = 2x as an example. We change the value of x in the equation to obtain the matching value of y to plot this equation on the graph. The ordered pair is made up of these x and y values (x, y). To obtain at least three ordered pairings, we repeat this for various x values.
Facts of Origin
By adding x = 0 to an equation, we can determine if the graph of the equation will pass through the origin. The equation’s line will pass through the origin if you arrive at y = 0.
Practical Applications of Origin
The origin is undoubtedly a crucial tool in mathematics, but it also has a lot of real-world applications. The following are a few examples of how the origin can be applied in actual life:
- Navigating Maps – In order to navigate maps and arrive at a destination, we need a fixed reference point. We will start at this location. This might be where we are right now or possibly a safe house on the way. In order to find and go to specific locations, we will subsequently be able to calculate the distances and directions from this starting point.
- Building – Structure construction requires a point of origin so that the right precautions may be taken and there is no error in the placement of bricks and beams throughout the structure. The building may collapse if the distances between such sites and the origin are not calculated properly.
- Missile or Rocket Launch –With precise origin positioning, missile or rocket launches can be carried out more efficiently. Torpedoes and other guided weapons employ the idea of origin to mark their targets.
- Location of Tsunami – Seismologists employ the idea of origin to precisely pinpoint the time and distance between intervals and regions where tsunamis occur.
- Dolphins and Bats Navigation – Dolphins and bats use sonic waves to navigate, and because the waves come from them, they can nearly precisely estimate what’s in their path.
Conclusion
In mathematics, the idea of origin is crucial, and it should be thoroughly grasped and internalized because it is useful in everyday life as well. This idea is fundamental to many calculations, and it is crucial for determining measurement accuracy.
Examples
Example 1
Determine the distance of the point -10 from the origin on a number line.
Solution
The position -10 from the origin, or 0 on a number line, is 10 units away.
Example 2
Calculate the separation between points (0, -7) and the origin.
Solution
The distance of (0, -7) from (0, 0)=-7=7 units.
Example 3
Where does the Cartesian Plane come from?
Solution
The origin of the Cartesian Plane is the intersection of the two axes. The symbols for the origin’s coordinates are (0, 0).
Example 4
What are the origin’s coordinates on the Cartesian Plane?
Solution
The origin is represented on the Cartesian Plane by the coordinates (0, 0), which indicates that both x and y are zero.
All images/mathematical drawings were created with GeoGebra.
