JUMP TO TOPIC
Parallelogram|Definition & Meaning
Definition
A quadrilateral that has 2 pairs of sides that are parallel to one another is called a parallelogram. The lengths of the different sides of a parallelogram are equivalent to one another, and the opposite angles have the same degree of measurement. Additionally, the interior angles located on the same plane of the transversal are considered supplementary. The whole amount of interior angles add up to a total of 360 degrees.
What Is a Parallelogram?
The English word “parallelogram” was taken from this Greek word. As a result, a parallelogram is defined as a quadrilateral with parallel lines serving as its boundaries. It is a shape that has opposite sides that are parallel to one another and are of equal length.
Each of the three primary forms of parallelograms—square, rectangle, and rhombus—is distinguished by a distinct set of characteristics distinct from the others.
In this article, we will study what a parallelogram is, how to calculate the area of a parallelogram, as well as other topics connected to parallelograms, followed by several instances that have been solved.
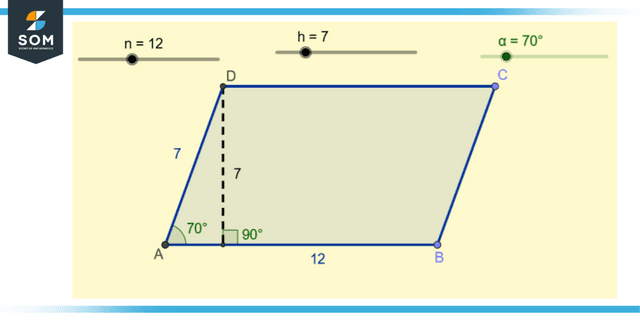
Figure 1: Representation of a parallelogram
Shapes of a Parallelogram
A parallelogram is a shape that only exists in two dimensions. It possesses a total of four sides, two pairs of which are parallel to one another. Additionally, the lengths of the sides are identical. The form in question is not a parallelogram if the lengths of the parallel sides do not measure the same. Similarly, the parallelogram’s inner angles opposite one another should always be equivalent. In such a case, we cannot call it a parallelogram.
Special Parallelograms
Both square and rectangular: Two more shapes comparable to a parallelogram in terms of their qualities are a square and a rectangle. Both opposing sides are of the same length and run parallel. Both shapes can be cut in half along their respective diagonals.
Rhombus
A rhombus is defined as a parallelogram in which all of the sides are congruent with one another or are equal.
Rhomboid
A rhomboid is a specific example of a parallelogram in which the sides that are perpendicular to each other are also parallel to the sides that are adjacent to them, but the lengths of the sides that are perpendicular to each other differ. In addition, each angle adds up to precisely 90 degrees.
Trapezium
A shape is said to be a trapezium if it has one pair of sides parallel to one another and the other two sides are not parallel to each other.
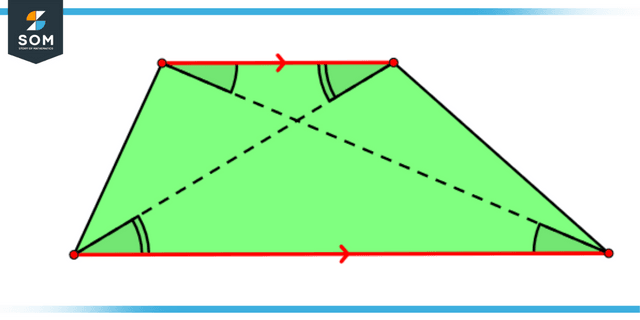
Figure 2: Representation of a Trapezium.
Angular Measurements of a Parallelogram
A parallelogram is a type of two-dimensional form that is flat and has four angles. Equal treatment is accorded to the opposing inner angles. The angles that are on the identical side of the transversal are complementary, indicating that their sum is equal to 180 degrees. Therefore, the total amount of angles that are contained within a parallelogram is equal to 360 degrees.
Parallelogram’s Characteristics and Attributes
- A unique kind of polygon known as a parallelogram is formed when a quadrilateral has two parallel sides and faces in opposite directions. The following is a list of the characteristics of a parallelogram:
- The different sides are parallel and equivalent
- Equal to each other is the diagonal
- The angles that are successive or adjacent to one another are complementary.
- In the event that any of the angles is a right angle, then the remaining angles will also be right angles.
- Both diagonals meet and cut each other in half.
- Each diagonal cuts the parallelogram in half, creating two congruent triangles.
- A parallelogram has a unique property in which the sum of the squares of all sides is equivalent to the sum of the squares of its diagonals.
Parallelogram’s Area
The space enclosed by all four parallelogram’s sides is referred to as the parallelogram’s area. It is possible to calculate, given the length of the parallelogram’s base and the height of the parallelogram.
Take into consideration the parallelogram RSTU with the base symbol (b) and the height symbol (h). It is possible to get the area of the parallelogram by applying the following formula: The area of a parallelogram is equivalent to the base times the height (h)
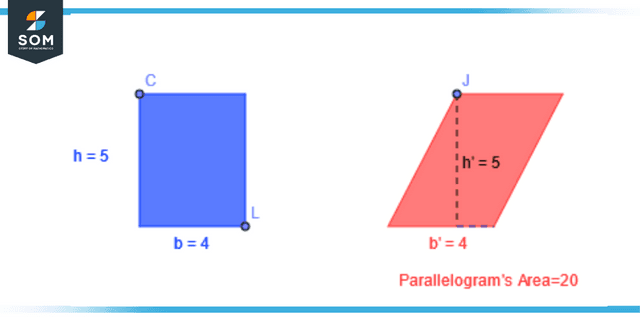
Figure 3: Representation of area of a parallelogram.
Parallelogram’s Perimeter
The length of the shape of a parallelogram is its perimeter; hence, the perimeter is equal to the total of all of the parallelogram’s sides.
Therefore, the formula for calculating the perimeter of a parallelogram with sides is:
P = 2 (a + b) units
Example Problems Involving Parallelograms
Example 1
A parallelogram has two adjacent angles of 4:5. Find each of its angles measurement.
Solution
Let the parallelogram be EFGH.
Then ∠E and ∠F are the adjacent angles.
Let:
∠E = (4x) ° and ∠F = (5x) °
We know that the sum of the adjacent angles of a parallelogram is equal to 180°, so:
∠E + ∠F = 180°
4x + 5x = 180
9x = 180
x = 20
Now:
∠E = (4*20) ° = 80°
∠F = (5*20) ° = 100°
∠F + ∠G = 180° (as ∠F and ∠G are adjacent angles)
100 + ∠G = 180°
∠G = 180° – 100°
∠G = 80°
Also:
∠G + ∠H = 180°
80° + ∠H = 180°
∠H = 180° – 80°
∠H = 100°
Therefore, ∠E = 80°, ∠F = 100°, ∠G = 80°, ∠H = 100°
Example 2
Consider a parallelogram ABCD in which ∠B = 45°. Find the measure of each of the angles ∠A, ∠C, and ∠D.
Solution
In the given parallelogram ABCD, ∠B = 45°.
The total sum of any two adjacent angles is 180°, so:
∠A + ∠B = 180°
∠A + 45° = 180°
∠A = (180° – 45°) = 135°
Also, we know that:
∠B + ∠C = 180°
45° + ∠C = 180°
∠C = (180° – 45°) = 135°
Furthermore:
∠C + ∠D = 180° [since ∠C and ∠D are adjacent angles]
135° + ∠D = 180°
∠D = (180° – 135°) = 45°
So, ∠A = 135°, ∠C = 135° and ∠D = 45°.
All images/graphs are created using GeoGebra.
