JUMP TO TOPIC
Parallel Lines|Definition & Meaning
Definition
Parallel lines are planar lines that never intersect. They always have the same space between them. Parallel lines are two or even more lines located in the same planes but never intersect. They are equal in distance and share the same slope.
Parallel lines are coplanar lines and do not cross at any point. Parallel planes comprise planes that never intersect in the same tri-space. Parallel curves do not touch or intersect and maintain a constant minimum distance. The yellow and red line segments are parallel here.
Figure 1 below shows two parallel lines.
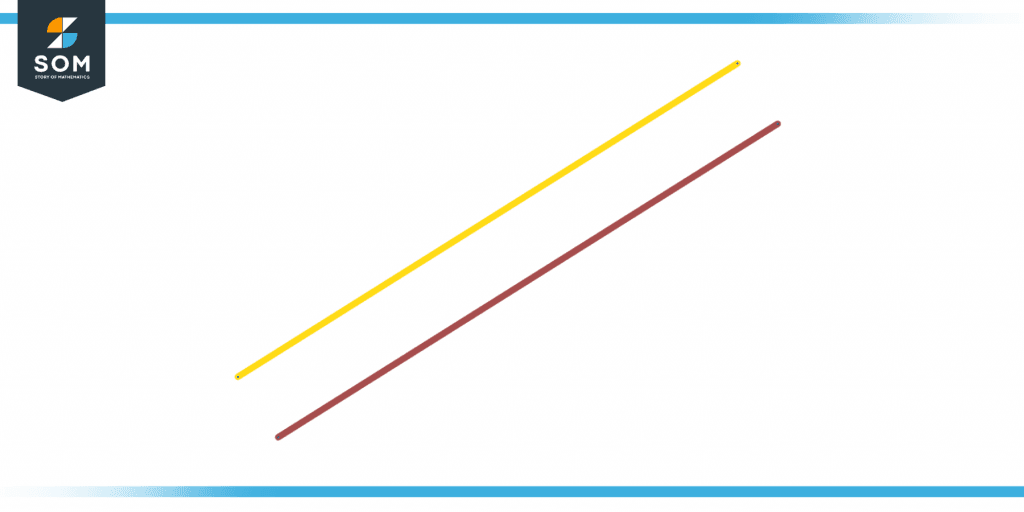
Figure 1 – Representation of a parallel line.
Parallel Lines and Transversal
Many angles are generated when two main parallel lines are joined by another line, known as a transversal. Some angles are identical (equal), whereas others are supplementary (different). Examine the image below to observe the parallel lines designated Line1 and Line2, broken by a transverse. Two intersecting lines and a transversal have generated eight distinct angles. An alphabet has been used to mark each angle.
Transversal
A transversal is a line that connects two lines in the same plane with two different places in the geometry. A transversal junction with two lines generates a variety of angles in pairs, including successive internal angles, matching angles, and alternative angles.
Figure 2 below shows the transversal cutting of 2 parallel lines.
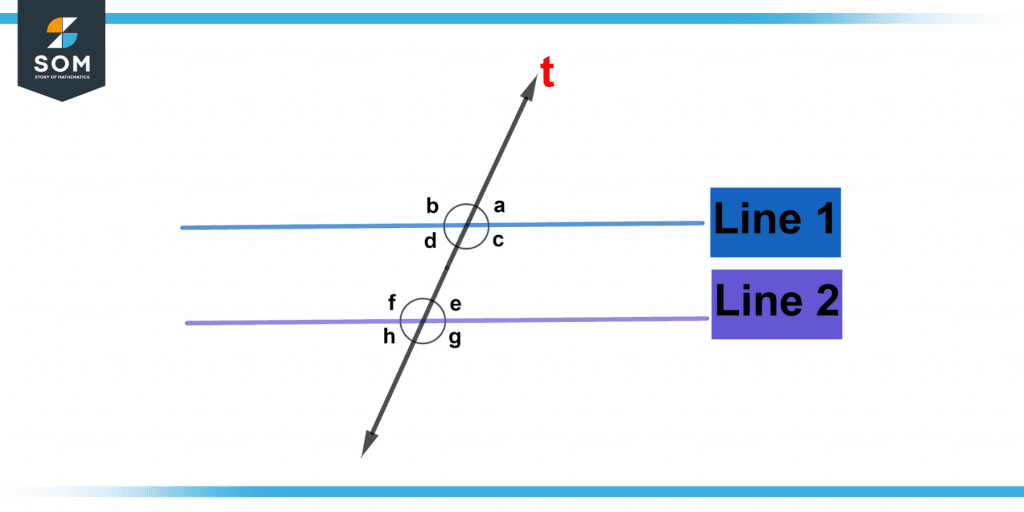
Figure 2 – Representation of angles in a parallel line.
The angles created by the two lines, Line 1 and 2, are shown below.
Corresponding Angles: It should be noted that the collection of similar angles is the same size. The following diagram shows four comparable angle pairings: an Equals e, b Equals f, c Equals g, and d Equals h.
Alternative interior angles are created inside the second line intersecting by a transversal. They are both the same size. c equals e in this figure, while d equals f.
Consecutive Internal Angles: Consecutive interior angles, also known as co-interior angles, are extra angles produced inside the transversal. In this case, c + f = 180° and d + e = 180°.
Vertically Opposing Angles: Vertical position opposite angles are generated when two equal-length straight lines collide. In this case, a = c, b = d, e = g, and f = h.
Properties of Parallel Lines
The essential qualities listed below make it simple to identify parallel lines.
- The term “independent” refers to someone who does not work for the government.
- Parallel lines never intersect, no matter what. They’re stretched in either direction.
- They are usually straight lines with equal spacing between them.
- They are parallel lines.
- They never cross, no matter how far you stretch them in any direction.
- A transversal line intersecting parallel lines on two separate locations will generate four angles at every point.
- The angles created by two parallel lines and a transversal are the same.
- Internal angle pairs on the same side of a crossing are supplementary.
- The angles that are vertically opposite/apex angles are equal.
- Alternate inner angles are equivalent.
How Can You Tell Whether Two Lines Are Parallel?
Apart from the features described above, it may be distinguished by the following attributes when a transversal intersects two parallel lines.
- Any two lines are considered parallel if, indeed, the angles created by them are equal.
- If the Opposite interior angles created by two lines are equal, they are referred to as parallel.
- If the Opposite exterior angles created by two lines are equal, they are referred to as parallel.
- If the Sequential interior angles located on the same face of the transverse are additional, lines are considered to be parallel.
Equation of Parallel Lines
A straight line equation is usually stated in the slope-intercept form, which is represented by the equation y = mx + b, where ‘m’ is the slope & ‘b’ is the y-intercept. The slope and gradient of the line are determined by the value of ‘m,’ which informs us how steep it is.
It is important to remember that the gradient of any pair of parallel lines is the same. For instance, if the gradient of a curve with equation y Equals 4x plus, three is 4. As a result, every line parallel with y Equals 4x Plus 3 has the same slope, which is 4. Parallel lines have distinct y-intercepts and share no points.
The Symbol for Parallel Lines
Parallel lines are indeed the ones that never intersect one another, no no matter how far we extend them. Parallel lines are represented by the symbol ||. AB II PQ, for example, denotes that section AB is perpendicular to line PQ. The symbol represents non-parallel lines ∦.
Figure 3 below shows the symbol for parallel lines.

Figure 3 – Sign for representing a parallel line.
Examples of Parallel Lines
Some of the examples are given below
Example 1
Are the lines crossed by a transversal with a 45-degree angle a and a 47-degree angle d parallel?
Solution
To produce parallel lines, the alternate, corresponding, and sequential angles must be the same, according to the characteristics of parallel lines.
In this instance, it is not the case, so the two lines aren’t parallel.
Example 2
Name two sets of angles created whenever a transversal intersects two parallel lines.
Solution
Several pairs of such angles are created whenever a transversal slices two parallel lines. Two of them include Corresponding angles & Alternate interior angles.
Example 3
Determine whether or not the provided lines are crossed by the transversal with both angles an at 95-degree and another angle b at 95-degree parallel.
Solution
The two lines are parallel because they satisfy one of the parallel line characteristics. “when the alternative interior angles are identical, the lines are parallel.”
Angle an equals angle b, and both are alternative interior angles.
This demonstrates that the two lines run parallel.
All images are made using GeoGebra.
