JUMP TO TOPIC
Parallel|Definition & Meaning
Definition
Two lines or line segments are said to be parallel to each other, if the perpendicular distance between their lines remains same throughout their length.
Two lines are called parallel to each other if we can prove that the perpendicular distance between them at all points is the same, they do not intersect each other at any point, they are pointing in the same direction, and they never converge or diverge.
All of the above conditions are basically describing the same thing in different words. The underlying mathematical condition or constraint remains the same. The following figure shows two line segments that are parallel to each other.
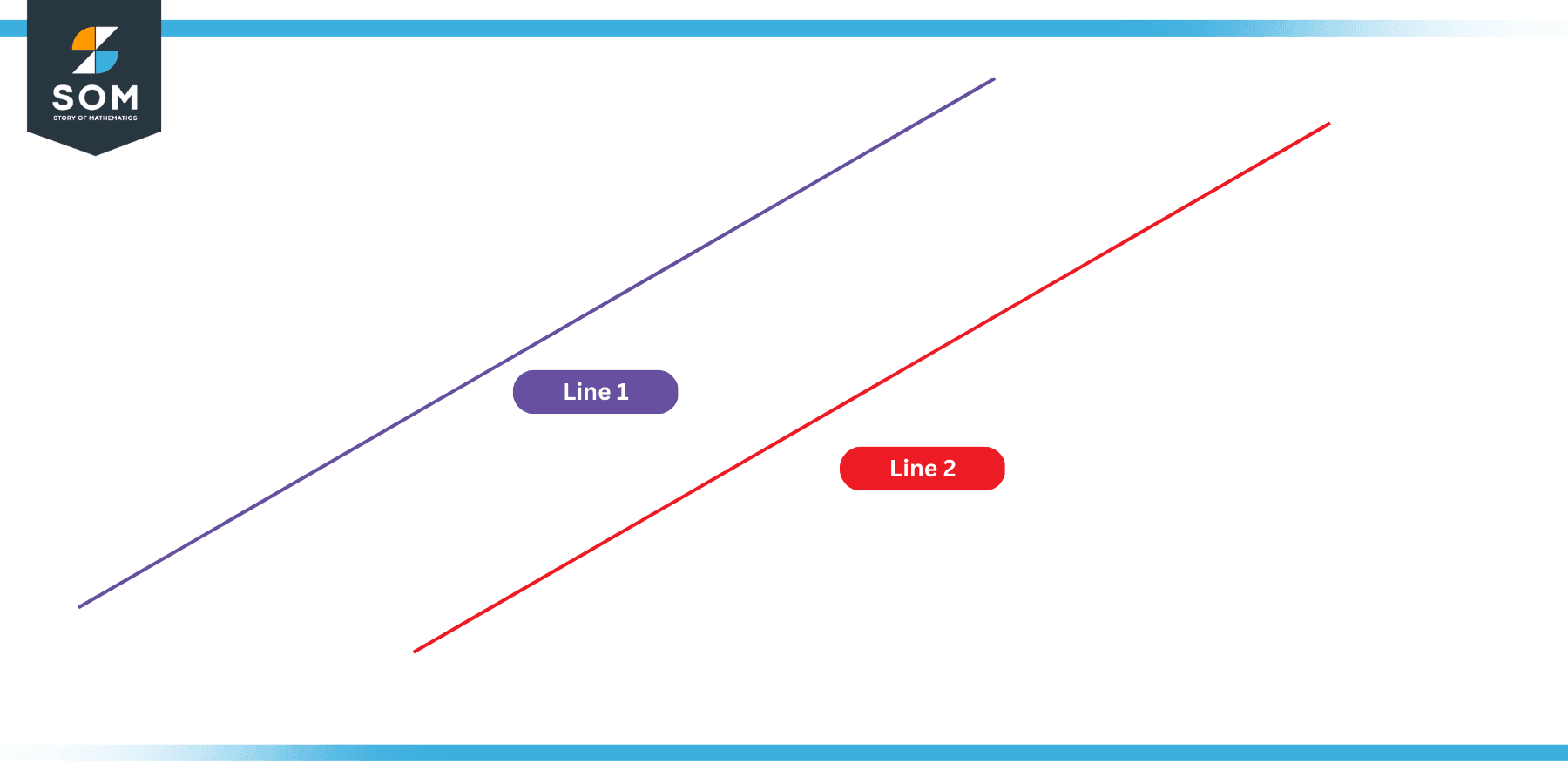
Figure 1: Two Parallel Lines
It can be seen clearly that both lines have the same direction, all points on both lines have equal perpendicular distance from the adjacent line, the are neither converging nor diverging, and, definitely they do not seem to have any point of intersection (at least not in the frame).
Explanation of Parallel Lines
The Greek Posidonius is credited by Proclus with defining parallel lines as equally spaced lines. However, the modern concept of parallelism was formalized by Euclid’s parallel postulate, which focuses on parallel lines.
In the perspective of geometry in particular and mathematics in general, parallel lines may be classified as co-planar straight lines that do not cross each other at any point. In other words, any pair of co-planer lines that do not intersect are termed parallel lines. This concept can easily be extended to planes.
That is, any pair of planes in the same three-dimensional space that never cross each other are said to be parallel planes.
There is a predetermined minimum separation or perpendicular distance between parallel lines that they maintain from minus infinity to plus infinity, and they do not touch each other or converge at any point. In three-dimensional Euclidean space, a line and a plane are said to be parallel if they do not share a point.
On the other hand, the intersection of two non-co-planar lines results in skew lines.
The parallel lines are important because of the unique set of deductions and geometrical laws that they follow. They help us as reference objects in many geometrical problems and help simplify more complex problems. One example of this kind of geometry is euclidean geometry, and parallelism is a characteristic of affine geometries.
Similar parallelism qualities may be seen in lines in other geometries, such as hyperbolic geometry.
Real-life Examples
Parallelism is very common in many real-world applications. The figure given below lists two such common examples.
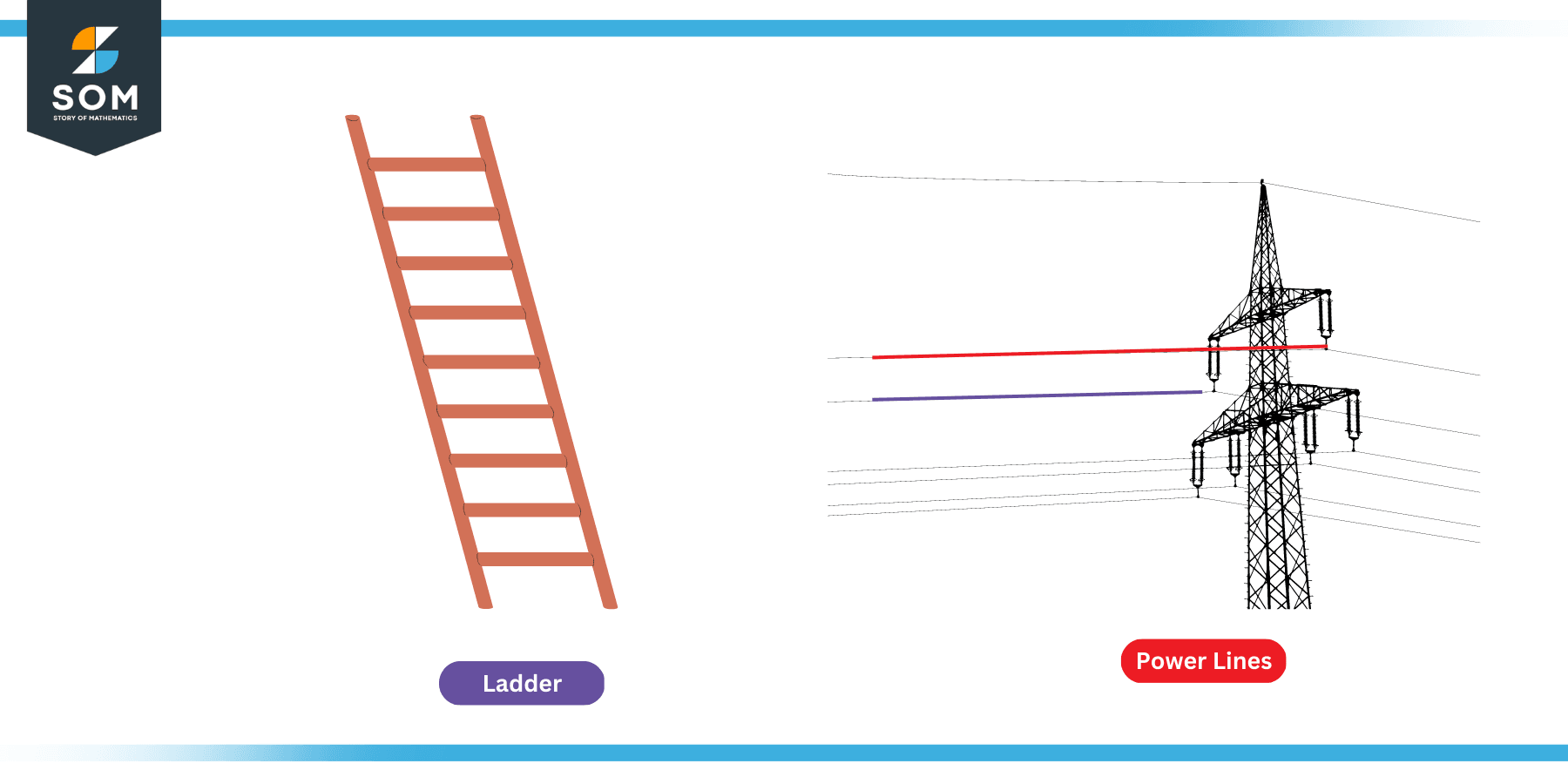
Figure 2: Real-Life Examples of Parallel Lines
Here you can see on the left in the figure that there is a ladder. The vertical supports of the ladder are parallel to each other. If they were not parallel, they would not support each other, and the structure would break. The rungs of this ladder represent the perpendicular distance between the lines passing through the supporting legs.
These rungs are also parallel to each other. Notice that the distance between the parallel supports remains the same throughout the length of the ladder, which is proven by the fact that the length of the rungs remains the same.
The figure shows a transmission line on the right side. It can be noticed that the hanging power lines on the transmission supports are also parallel to each other. Two such lines are highlighted in red and blue color for clarity.
The perpendicular distance between these lines is kept constant and is depicted by the cross arm length of the supporting tower that, as we know, remains constant.
Euclidean Postulates of Parallelism (Properties of Parallel Lines)
In this section, we present a more mathematically rich perspective of parallelism with respect to straight lines. We formally introduce parallelism and the properties of parallel lines in the following paragraphs. These properties can also be used to verify or check whether two lines are parallel or not.
(a) For two lines to be parallel, each point on one of the lines must maintain a constant minimum distance from the other line. That is, both lines should maintain equal distance at all points.
(b) For two lines to be parallel, there must not exist any point that satisfies both line equations. That is, there shouldn’t exist any point of intersection or the lines must never converge.
(c) If a straight line crosses two parallel lines, the corresponding angles created by this line with both of the parallel lines must be congruent. Congruent means that the angles will be identical to each other. This property is explained in the following figure.
(d) For two lines to be parallel, they must have the same slope.
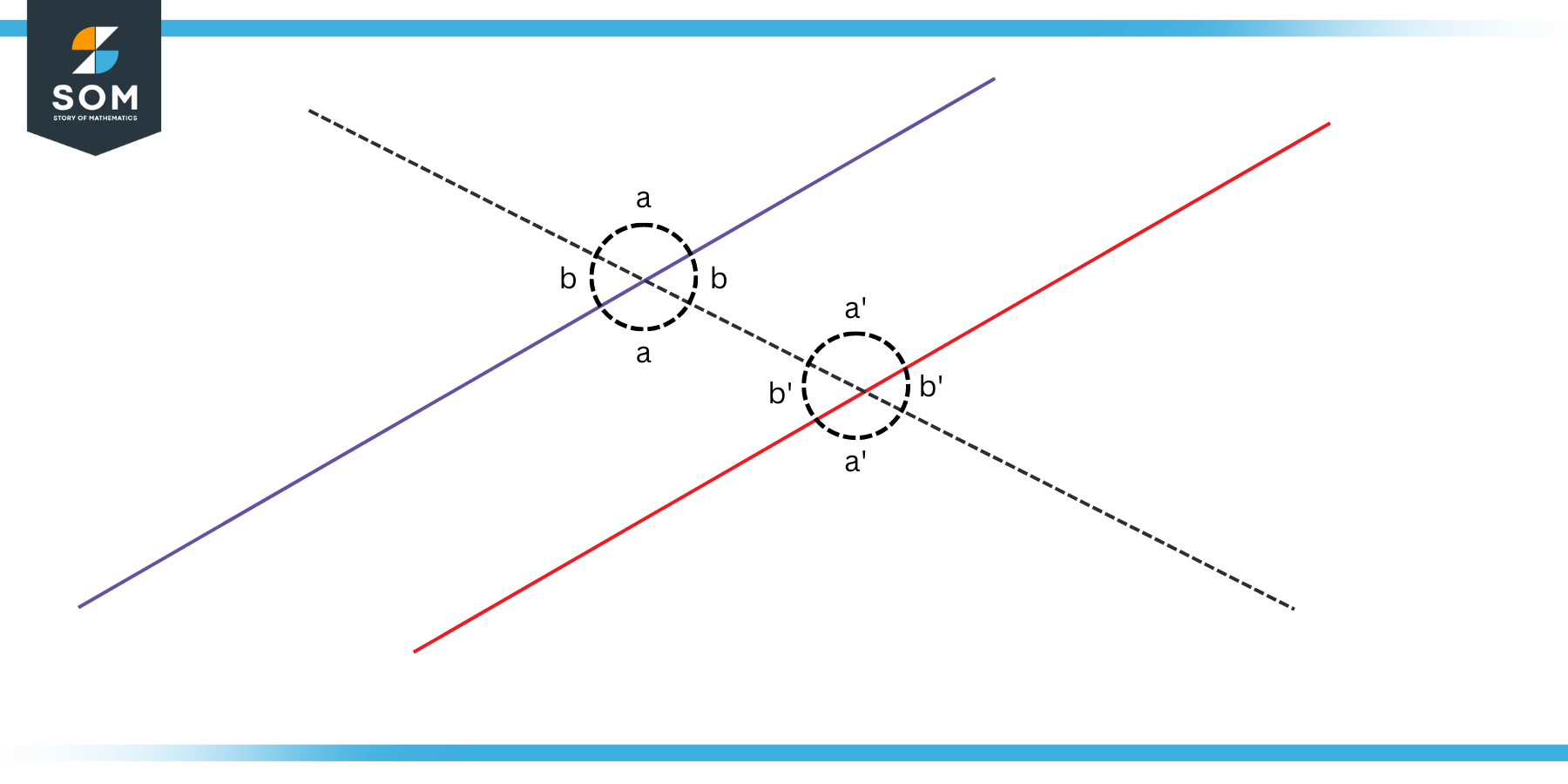
Figure 3: Line Crossing two Parallel Lines
Now in this figure, the red and blue lines are parallel if and only if the pair of angles a, a’ and b, b’ are congruent (equal).
This means that if you draw a line such that it crosses two lines, as shown in the figure, and you somehow prove that such corresponding angles are equal, then it is a proof that the lines are parallel.
The first and third criteria are “more complex” than the second since they require measurement, although any of these related features might be used to locate parallel lines in euclidean space. As a result, in euclidean geometry, parallel lines are often represented by the second characteristic.
The effects of Euclid’s Parallel Postulate are the other features. The same gradient between parallel lines may serve as another characteristic of measurements (slope).
Calculation of Distance Between Two Lines
There is a certain distance between the two parallel lines because parallel lines in a Euclidean plane are identical in length. Given the equations for two parallel non-vertical lines, by locating two points (one on each line) that are perpendicular to one another and figuring out their distances, it is possible to determine the distance between the two lines.
Let us say that two lines are represented in the slope-intercept form as follows:
$ y = mx + u_1 $
$ y = mx + u_2 $
Notice that the slope is kept the same (i.e., m) since the lines are parallel. The distance between these two lines is given by the following formula:
\[ d = \dfrac{ | u_1-u_2 | }{ \sqrt{ m^2 + 1 } } \]
If two lines are represented in the form of the standard form as follows:
$ a x + b y + c_1 = 0 $
$ a x + b y + c_2 = 0 $
Notice that for parallel lines, a and b must remain the same. The distance between these two lines is given by the following formula:
\[ d = \dfrac{ | c_1-c_2 | }{ \sqrt{ a^2 + b^2 } } \]
The following figure summarizes all these formulae:
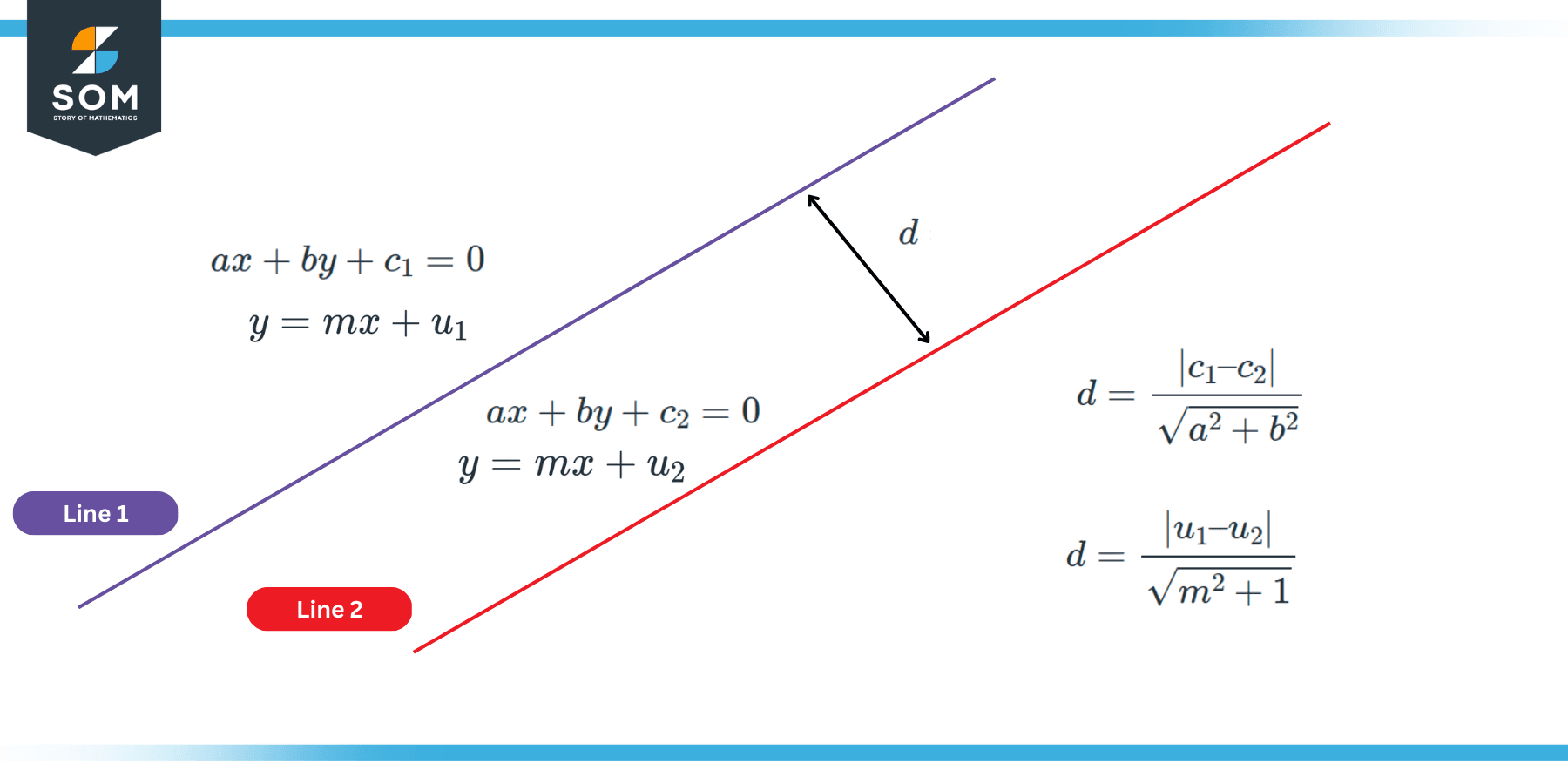
Figure 4: Distance Between Two Parallel Lines
Numerical Problems
Part (a): Find the distance between parallel lines represented by 4x + 3y + 4 = 0 and 4x + 3y + 24 = 0.
Part (b): Find the distance between parallel lines represented by y = 10x + 2 and y = 10x +10.
Solution to Part (a)
Given:
Line 1: 4x + 3y + 4 = 0
Line 2: 4x + 3y + 24 = 0
Comparing with standard line equation:
$ a $ = 4, $ b $ = 3, $ c_1 $ = 4, $ c_2 $ = 24
Using the formula:
\[ d = \dfrac{ | c_1-c_2 | }{ \sqrt{ a^2 + b^2 } } \]
Plugging the values:
\[ d = \dfrac{ | 24-4 | }{ \sqrt{ 4^2 + 3^2 } } \]
\[ d = \dfrac{ | -20 | }{ \sqrt{ 25 } } \]
\[ d = \dfrac{ 20 }{ 5 } \]
\[ d = 4 \]
Solution to Part (b)
Given:
Line 1: y = 10x + 2
Line 2: y = 10x + 10
Comparing with the slope-intercept form:
$ m $ = 10, $ u_1 $ = 4, $ u_2 $ = 24
Using the formula:
\[ d = \dfrac{ | u_1-u_2 | }{ \sqrt{ m^2 + 1 } } \]
\[ d = \dfrac{ | 2-10 | }{ \sqrt{ 10^2 + 1 } } \]
\[ d = \dfrac{ | -8 | }{ \sqrt{ 101 } } \]
\[ d = \dfrac{ 8 }{ 10.05 } \]
\[ d = 0.796 \]
All images were created with GeoGebra.
