Parabola|Definition & Meaning

Components of Parabola 

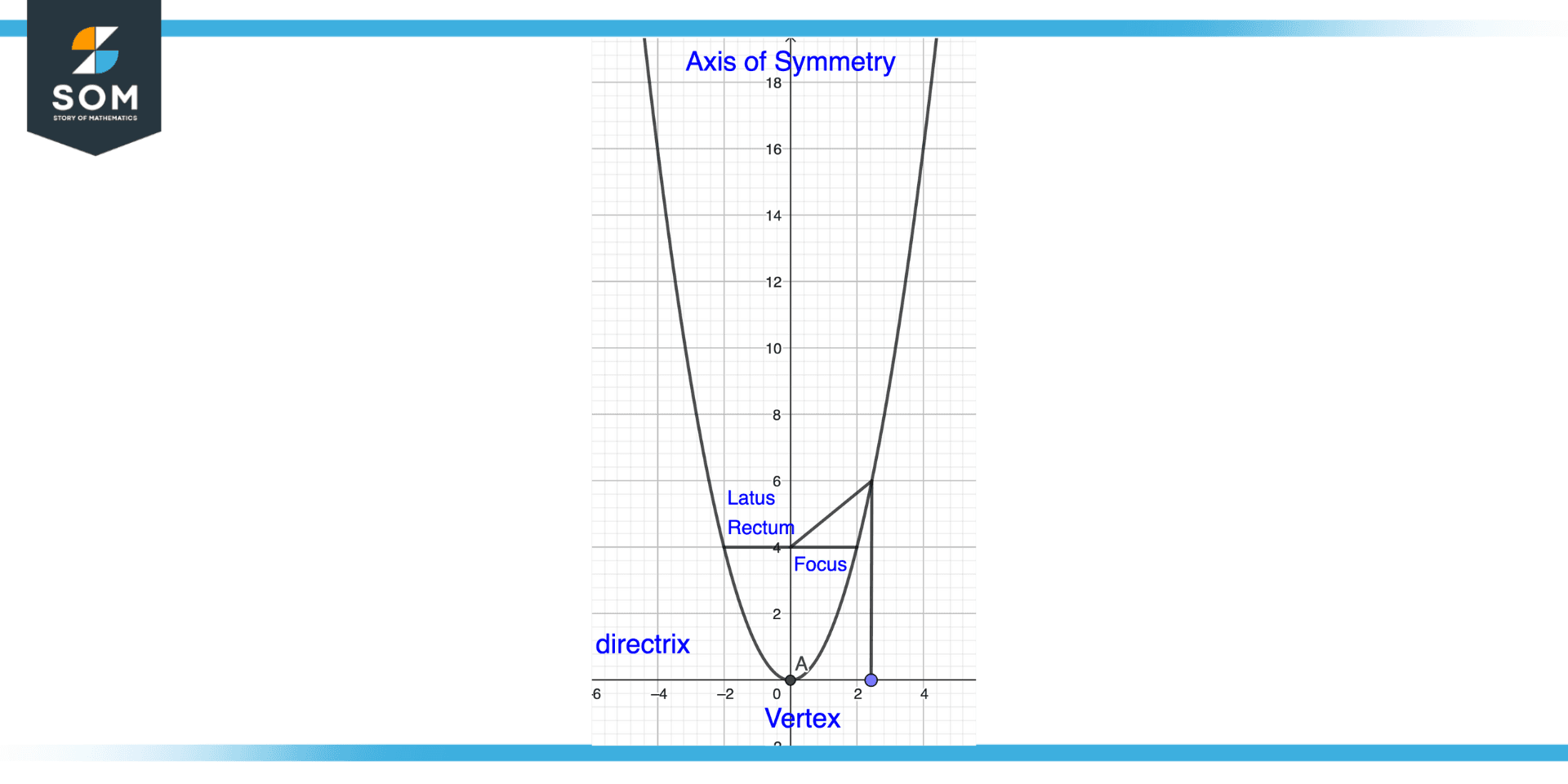
Figure 1 – Components of Parabola

The components of the parabola are illustrated in the figure above.

1. Axis of symmetry: The line that splits the parabola into two identical halves is known as the axis of symmetry. The directrix and the axis of symmetry are always perpendicular.
2. Vertex: The parabola’s highest or lowest point is known as the vertex. The parabola’s vertex is the point closest to the focus.
3. Focus: The location on the axis of symmetry that serves as the parabola’s definition. All the points that are equally spaced apart from the focus and the directrix make up the parabola.
4. Directrix: The line that serves as the parabola’s definition. All the points that are equally spaced apart from the focus and the directrix make up the parabola.
5. Latus Rectum: The latus rectum is the portion of the parabola that passes through the focus while being perpendicular to the axis of symmetry. The latus rectum determines the size and shape of the parabola.
6. Conjugate axis: The axis that traverses the focus while running perpendicular to the axis of symmetry. The parabola’s size and shape are determined by the conjugate axis.

Different Equations for Parabola

There are several different forms of the equation of a parabola that can be used, depending on the specific needs of the problem at hand.

1. Standard form: y = a(x – l)$^{2}$ + m, where (l, m) denotes the vertex of the parabola.
2. In Vertex form: y = a(x – l)$^{2}$, where (l, k) denotes the vertex of the parabola. This form is useful when the focus of the parabola is known and the vertex form is needed.
3. General form: y = ax$^{2}$ + bx + c, where a, b, and c are constants. This form is useful when the line of symmetry, or axis of symmetry, of the parabola, is known.
4. Factorized form: y = a(x – b)(x – c), where a, b, and c are constants and r and s are the roots of the equation. This form is useful when the x-intercepts of the parabola are known.
5. Parametric form: x = at$^{2}$ and y = 2at + b, where a, b, and t are constants. This form is useful when the focus of the parabola is known and the vertex form is not needed.
6. Polar form: r = at$^{2}$, where a and t are constants. This form is useful when the parabola is in polar coordinates.

Types of Parabola

There are two main types of parabolas: those that open upwards and those that open downwards. These types are illustrated in the figure shown below.

1. A mathematical equation of the form y = ax$^{2}$ + bx + c, where a > 0, defines an upward-opening parabola. This equation’s graph will be a parabola with an upward opening and a vertex at the bottom of the curve.

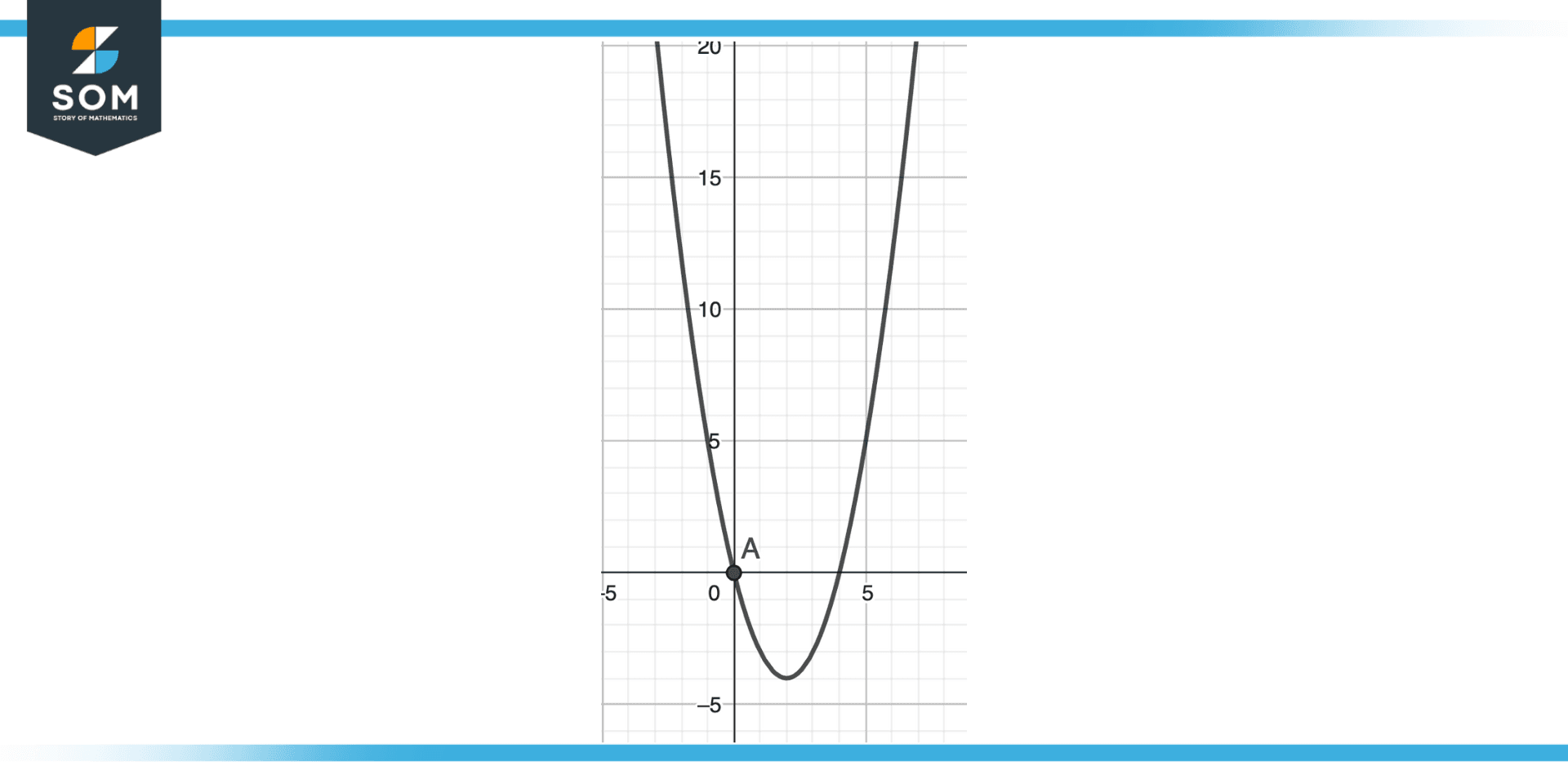
Figure 2 – Parabola Opening Upward

2. An equation of the form y = ax$^{2}$ + bx + c, where a < 0, describes a downward-opening parabola. The graph of this equation will be a downward-opening parabola, with the highest point on the curve serving as the vertex.

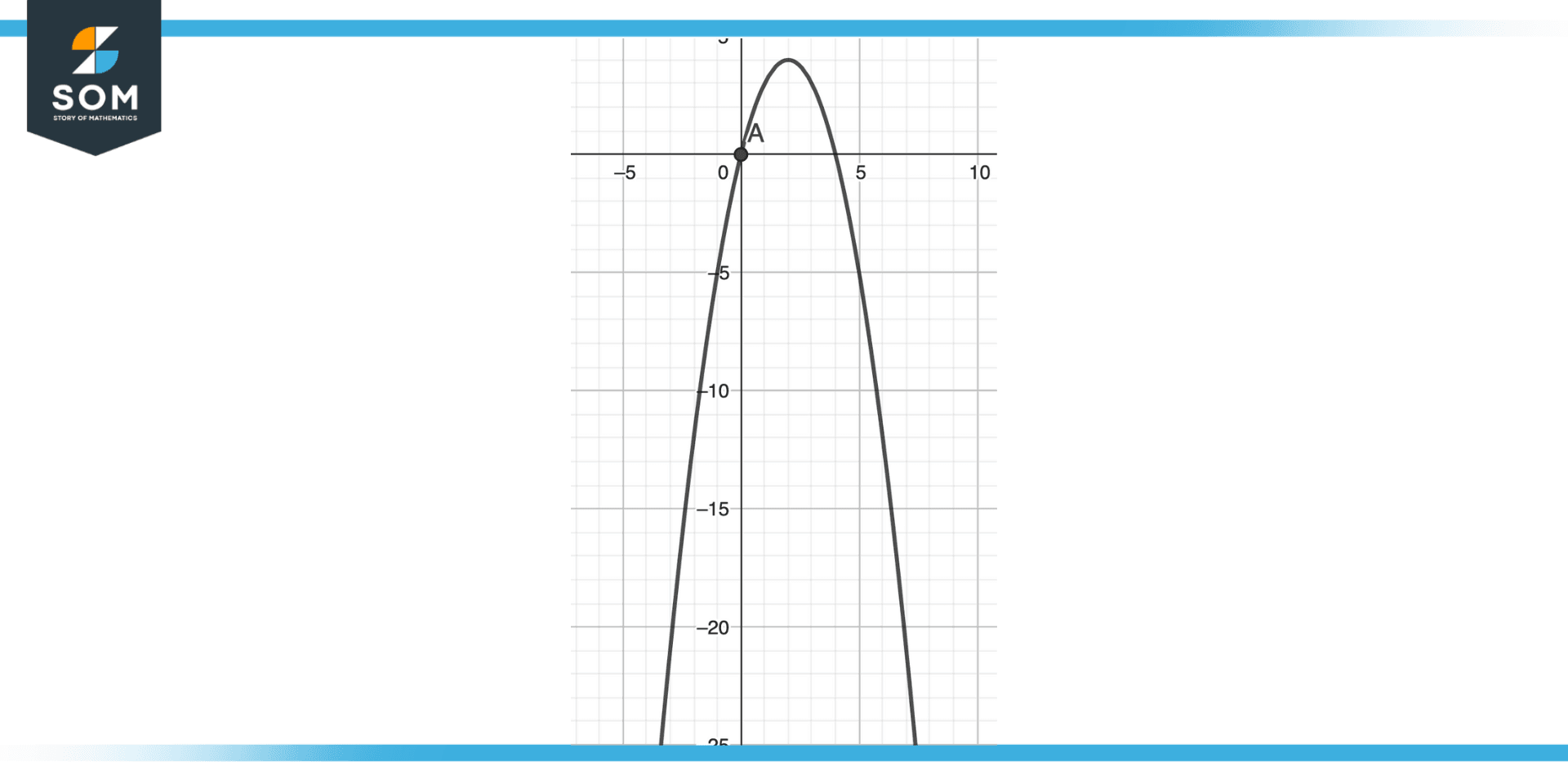
Figure 3 – Parabola Opening Downward

Graph of Parabola and Properties

The graph of a parabola has several important features.

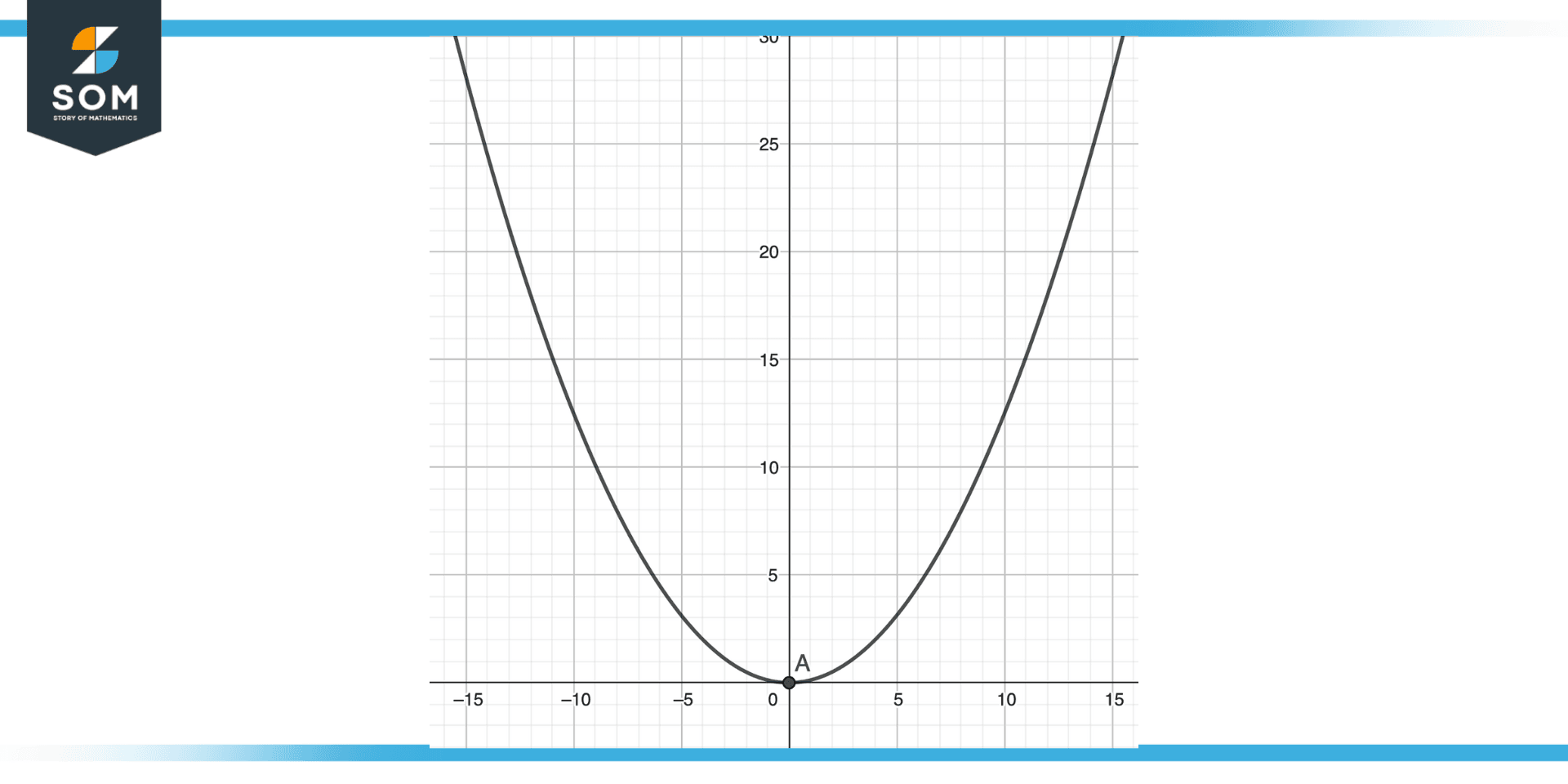
Figure 4 – Graph of Parabola

1. The vertex is either the highest point on the curve or its lowest point, depending on how the parabola opens. It is situated at the coordinates (h, k), where h and k represent the x- and y-values, respectively.
2. The axis of symmetry is the line that divides the parabola into two halves that are mirror images of one another. It runs across the vertex and is a line of symmetry for the parabola.
3. While the focus is a fixed point inside the parabola, the directrix is a line that is constantly outside the parabola. The focus and the directrix are equally distant from each point on the parabola.
4. Depending on the values of the variables a, b, and c in the equation, the parabola may intersect either the x-axis or the y-axis.

Application of Parabola

Parabolas have a wide range of applications in various fields, including mathematics, science, engineering, and technology. Here are a few examples:

1. Mathematicians use parabolas to represent and examine a wide range of phenomena, including the trajectory of a bullet and the power of sound waves.
2. In physics, parabolas are used to explain how objects move when they are affected by gravity. A parabolic curve, for instance, describes the path of a ball being thrown or a satellite in orbit.
3. When designing structures and equipment for the precise focus or reflection of light, sound, or other types of energy, engineers use parabolas. Headlamps, parabolic microphones, and satellite dish antennae are a few examples.
4. Buildings that can survive earthquakes and other types of structural stress are designed using parabolas in architecture.
5. Parabolas are used in finance to simulate, examine, and make investment decisions based on the behavior of the financial markets.
6. In sports, such as golf, soccer, and baseball, parabolas are used to study and optimize the trajectory of balls and other items.

Parabola in Conic Section

A parabola is a particular kind of conic section, a curve created by the intersection of a right circular cone and a plane. The ellipse, hyperbola, and circle are the other shapes that can have conic sections.

A parabola is the collection of all points that are equidistant from a particular point (the focus) and a particular line (the directrix). It can also be envisioned as the perpendicular to the cone’s axis cross-section of a right circular cone.

Solved Example of a Parabola

Example

Locate the parabola’s vertex according to the equation given by y = x$^{2}$ + 2x – 3.

Solution

To find the vertex of the parabola, we can rewrite the equation in vertex form: y = a(x – h)$^{2}$ + k.

To do this, we can complete the square:

y = x$^{2}$ + 2x – 3 = (x$^{2}$ + 2x) – 3 = x$^{2}$ + 2x + 1 – 4 = (x + 1)$^{2}$ – 3

So, the vertex of the parabola is at the point (h,k) = (-1, -3).

All mathematical drawings and images were created with GeoGebra.

Palindromic Numbers Definition < Glossary Index > Parallel Definition