JUMP TO TOPIC
Palindromic Numbers|Definition & Meaning
Definition
A palindromic numeral is a number that stays identical when its integers or characters are read in reverse order, i.e., a name, word, or number is called palindrome when it is read the same in a forward or backward direction.
A palindromic number is the same number that is read forward and backward. The instances of palindromic numbers are shown in Figure 1.
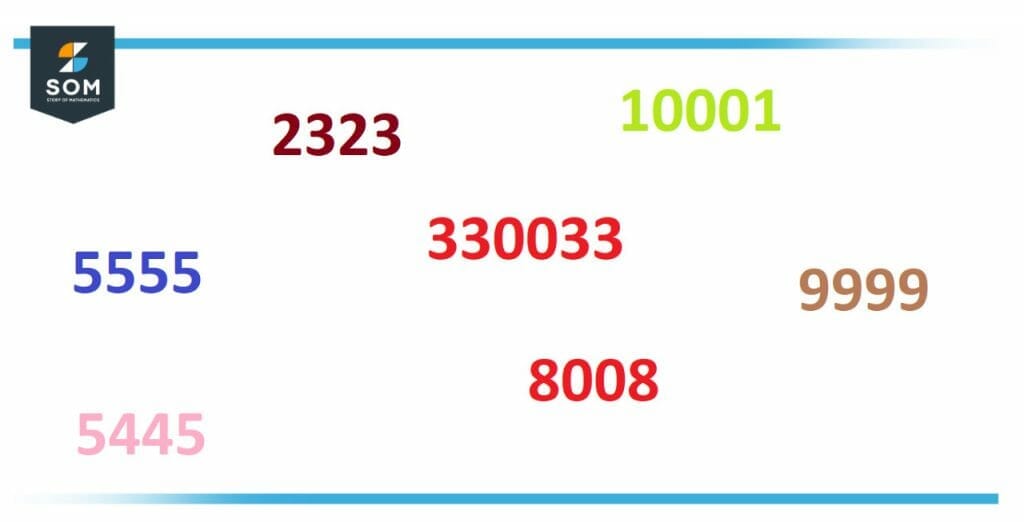
Figure 1: Palindromic Number Examples
A palindromic number, commonly referred to as a numeric or numeral palindrome, is a number (such as 16461) whose value does not change when its digits are flipped. It has reflection-al symmetry along a vertical axis, to put it another way.
The word “palindromic” comes from the word “palindrome,” which describes a word (like “rotor” or “race car”) whose spelling remains the same when its letters are flipped over.
A few of the palindromic numbers include 4, 44, 565, 434, 676, 909, 4004, 8998, 3443, 35453, 78987, 55, 2332, etc.
In the area of recreational mathematics, palindromic integers are the most studied. Commonly, a problem calls for palindromic numbers that also have a certain quality. For illustration, the prime numbers can also be palindromic, for example, 7, 5, 2, 11, 151, 101,… etc.
Also, the squares of some numbers can also be palindromic, for example, 4, 1, 0, 121, 9, 10201, 676, 12321, 484… etc.
It is clear that any base has an infinite sequence of integers written (in that base) as 101, 1001, 10001, 100001, etc., which proves that there are infinitely many palindromic numbers in every base. There can be instances of palindromic names, as shown in Figure 2 below.
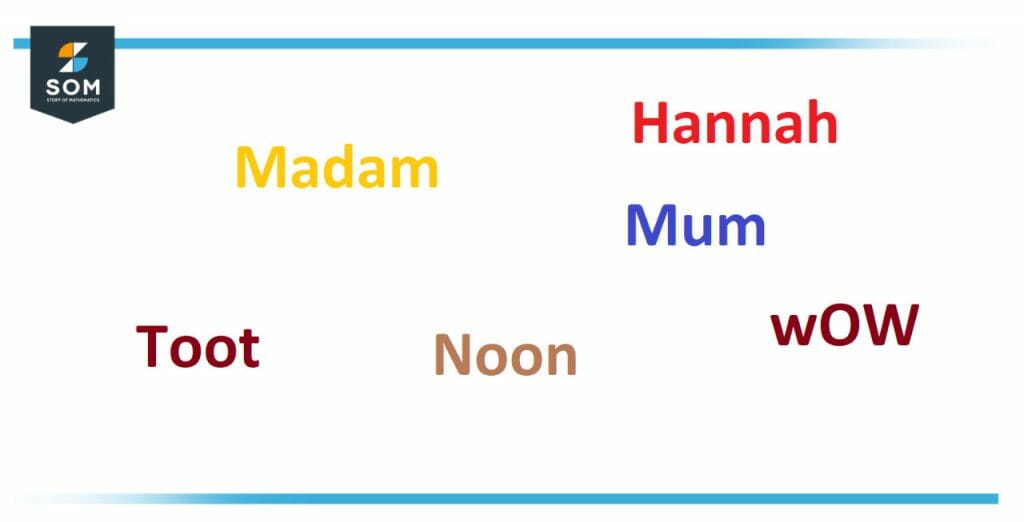
Figure 2: Palindromic Names
Figure 2 shows that the names or words consisting of alphabets can also demonstrate palindromicity, i.e., words read in a forward or backward direction can be identical.
Formal Definition
The concept of palindromicity can be used to describe natural numbers in any numeral system, even though palindromic numbers are typically thought of in terms of the decimal system. Consider the following conventional notation for a number n > 0 in base b ≥ 2, which is documented in the standard memo with k+1 digits $a_j$:
K = $\sum _{j=0}^i a_j b^j$
where, 0 ≤ $a_j$ < b for all i and $a_i$ ≠ 0. ‘K’ is palindromic iff $a_j$ = $a_{i−j} for all j.
Perfect Powers
There are many palindromic perfect powers $n_k$, where n represents the natural numbers and k can take the values 4, 3, or 2.
The examples of palindromic perfect squares, like the few of them given above, include 4, 1, 0, 121, 9, 10201, 676, 484, 12321, 44944, 10201… etc. and examples of palindromic perfect cubes include 0, 343, 1, 1331, 8, 1030301, 1003003001,… etc.
Similarly, examples of palindromic perfect fourth powers include 0, 1004006004001, 1, 104060401, 14641,… etc.
The only known non-palindromic number with a palindrome cube is 2201; it is hypothesized that all fourth powers of palindromes have a root that can be written in a closed-form formula. In contrast, it has also been discovered that no palindromes can exist for numbers that can be written in closed form $n_k$ for k > 4 (and n > 1).
A palindromic number is one that has the same value whether it is written forwards or backward (in a given base), i.e., of the form. As a result, a sequence of palindromic numerals can be written.
The figure above shows how many palindromic numbers there are that are smaller than a particular number. The smallest three-digit palindromic prime is 101.
In the Wolfram Language, Palindrome Q[n] can be used to determine whether a given integer is palindromic. Palindromic numbers that are less than 10 are 9, 18, 108, 198, 1098, 1998, 10998, etc. The closed-form formula yields this sequence. In their 2004 study, Banks et al. showed that practically all palindromes (in any base) are composite.
The value has been estimated using all of the palindromic numbers, and it is 3.370001832. The reciprocals of the palindromic integers added together converge to a fixed value. Few facts about palindromic numbers include:
- The first few palindromic pronic numbers are 2, 6, 272, 6006, 289982, and the first few pronic palindromic numbers are 1, 2, 16, 77, 538, 1621,…
- The initial numbers with palindromic squares are 1, 2, 3, 11, 22, 26,…, and the initial squares with palindromic numbers are 1, 4, 9, 121, 484, 676,…
- There are no palindromic square-digit numbers for, 4, 8, 10, 14, 18, 20, 24, 30,…
- There can be numbers that are not the sum of two palindromic numbers keeping in view that 0 is also a palindromic number.
- There can be numbers that are not the difference of two palindromes: 1029, 1020, 1038, 1031, 1047, 1041, 1061, 1051, …
Anti-palindromic Numerals
The number is said to be anti-palindromic if it remains identical when read in a forward or reverse direction as well as when it is subtracted from ‘b-1, it yields the original sequence again. When a natural number is decomposed into its digits $a_k$ in base ‘o’, a number is anti-palindromic if and only if $a_k$ = $o − 1 − a_{i − k}$. A few examples of the formation of palindromic numbers have been shown in Figure 3.
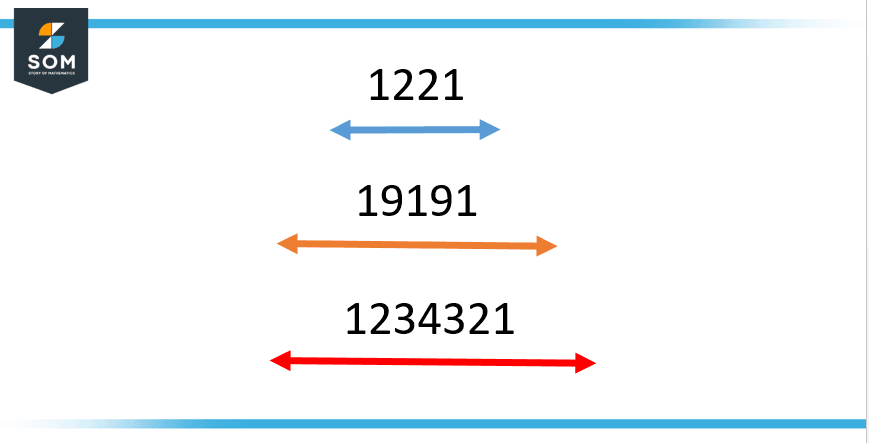
Figure 3: Formation of palindromic numbers
Sum of Palindromes and Sum of Their Reciprocals
The sum of the palindromic numbers’ reciprocals is a convergent series with a value of roughly 3.37028. Regarding sums, the following are a few facts about palindromic numbers:
- Every positive integer may be expressed as the sum of three palindromic integers in every number system with a base of 5 or more, according to research released in 2018.
- Any integer number is a sum of three palindromes having 10’s base.
- Every number can be written in palindromic form for some base. It is not limited to just one base number system.
Examples of Palindromic Numbers
Example 1
Write out some examples of palindromic words.
Solution
Examples of palindromic words include noon, civic, race-car, level, mom, etc.
Example 2
Write out some examples of palindromic numbers.
Solution
Examples of palindromic numbers include 9, 18, 108, 198, 1098, 1998, 10998, etc.
All images/mathematical drawings were created with GeoGebra.
