Perimeter|Definition & Meaning

A closed path that covers, outlines, or surrounds either a two-dimensional object or a one-dimensional length is referred to as the perimeter of that shape or length. The term “circumference” refers to the length of a circle’s or an ellipse’s perimeter. 

What Is Perimeter?

The calculation of the perimeter can be put to use in a variety of situations. The distance around a garden or yard that must be enclosed by a fence can be represented by its computed perimeter. The distance that a wheel or circle travels during one revolution can be determined from its perimeter, also known as its circumference.

In a similar manner, the quantity of string that is wound around a spool is proportional to its perimeter, so the string’s length was exactly the same as the perimeter.

Figure 1 – Area and Perimeter

The whole distance encircling a shape is referred to as its perimeter. It is the length of any 2-dimensional geometric shape’s boundary or outline. Depending on the size, the perimeter of several figures can be the same. Consider a triangle built of a certain length of wire, for instance, L.

If all the sides have the same length, so the same wire could be used to create a square. Look at the picture above, which shows the border of a square park.

Units of Perimeter

The perimeter of a shape is the shortest distance encircled by that boundary. Because of this, the perimeter will be expressed in the same units as the length. Perimeter is essentially a one-dimensional concept. It can therefore be quantified using a variety of different units, such as meters, kilometers, millimeters, etc.

Distances can also be measured in feet, yards, miles, and inches, all of which are widely recognized as valid systems of measurement.

Formula of Perimeter

The term “perimeter” refers to the complete length of the boundaries that surrounds a closed shape. Imagine a piece of chocolate that is square in shape and has a side length of one inch. The perimeter of every figure in two dimensions is calculated by summing all of the figure’s sides.

As a result, the circumference of a chocolate piece with a square shape measures 1 inch plus 1 inch plus 1 inch plus 1 inch, which equals 4 inches. The calculation for it is as follows: Perimeter = Sum of all Sides. The following passages below present the formulas for calculating the perimeters of several 2-dimensional figures.

Perimeter of Rectangle

The formula for calculating the perimeter of a rectangle is as follows: P = (L + W) $\times$ 2, where P stands for the perimeter, L stands for the length, and W stands for the width.

If you are provided with the length and width measurements of a rectangle, all you need to do to calculate its perimeter is insert those values into the appropriate spots in the appropriate formula.

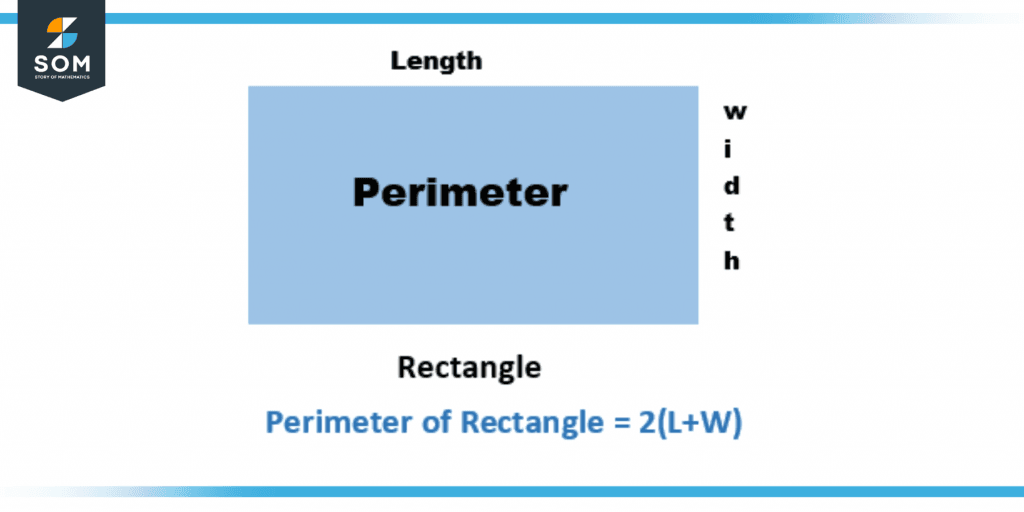
Figure 2 – Perimeter of Rectangle

For instance, if the given rectangle above depicts a garden that requires a brick boundary, we can employ the perimeter formula to calculate the total number of feet of the brick border that will be required.

Perimeter of Square

The distance around an open or closed geometric object is what is meant to be understood under the term “perimeter.” The distance that is traversed by all four of a square’s sides is referred to as its perimeter. In a flat, two-dimensional plane, the shape is surrounded or outlined by the perimeter.

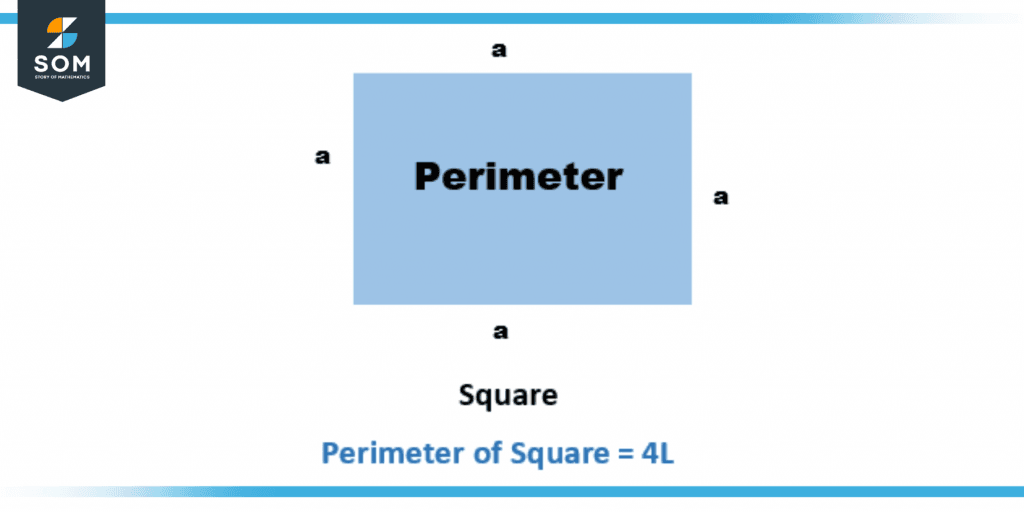
Figure 3 – Perimeter of Square

Because each of a square’s sides is the same length, the square’s perimeter may be calculated as four times the length of a side or 4 multiplied by the length of the side.

Perimeter of Circle

A circle’s boundary, also known as the total length of the arc of the circle’s periphery, is referred to as the circle’s perimeter. It is called a circle’s circumference, and it is the term that refers to the circle’s perimeter.

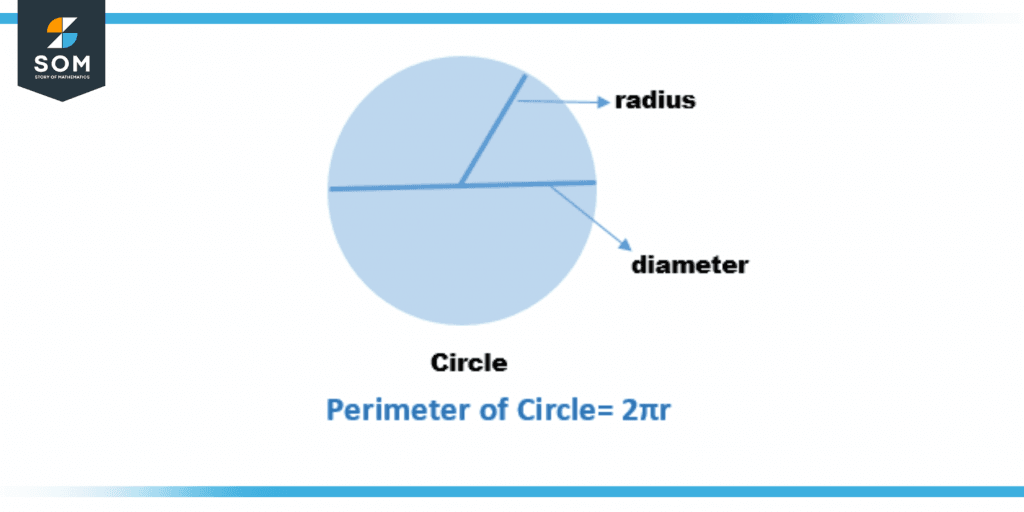
Figure 4 – Perimeter of Circle

The formula for calculating the perimeter of a circle is comprised of three components: two constants and one variable, which is the circle’s radius. The following is an example of a formula that may be used to determine either the circumference or the circle perimeter:

Perimeter of a circle = Circumference = 2πr = πD units

Here, r and D represent the circle’s radius and diameter, respectively.

Perimeter of Triangle

In most cases, the formula for calculating the perimeter of something like a closed shape will be the same as the length of the figure’s outer line. Therefore, the area of a triangle’s perimeter will be equal to the sum of all three of its sides if the triangle is a triangle. In the event that three sides of a triangle are labeled x, y, and z, respectively, then:

Perimeter P = x + y + z

Perimeter of an Equilateral, Scalene, and Isosceles Triangle

The perimeter of different triangles are different listed below is the figure which represents the perimeter of different triangles.

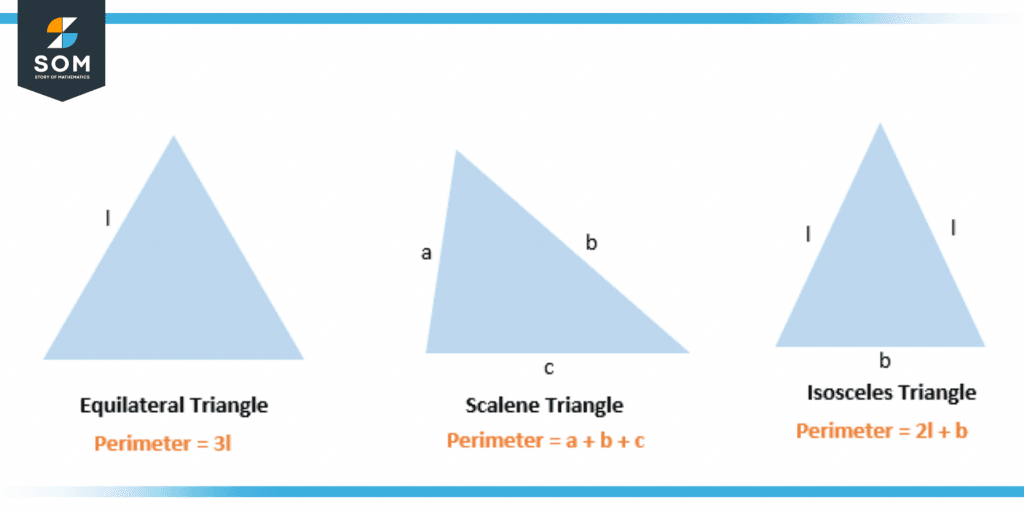
Figure 5 – Perimeter of Triangles

This figure represents the perimeter of the equilateral, scalene, and isosceles triangles, which simply shows the addition of all sides of the triangle.

Perimeter of Parallelogram

The perimeter can be calculated by adding together the lengths of each of the four sides. The total distance that lies outside of the confines of any parallelogram is denoted by the term “perimeter.” Since the opposing sides of it are equal to one another, the perimeter of the parallelogram is equal to two times the sum of its two parallel sides, which we will refer to as a and b. The perimeter of a parallelogram has the formula:

P = 2 (a + b) units.

Example of Perimeter Calculation

Determine the perimeter of a parallelogram with a base measurement of 9 centimeters and another side measurement of 14 centimeters.

Solution

b = 9 cm

a = 14 cm

Perimeter of a Parallelogram = 2(a + b)

= 2(9 + 14)

= 2 x 23 cm

= 46 cm

All the figures above are created on GeoGebra.

Perfect Square Definition < Glossary Index > Permutation Definition