Perfect Square|Definition & Meaning

Figure 1 shows a perfect square 49, which is the product of 7 with itself. 

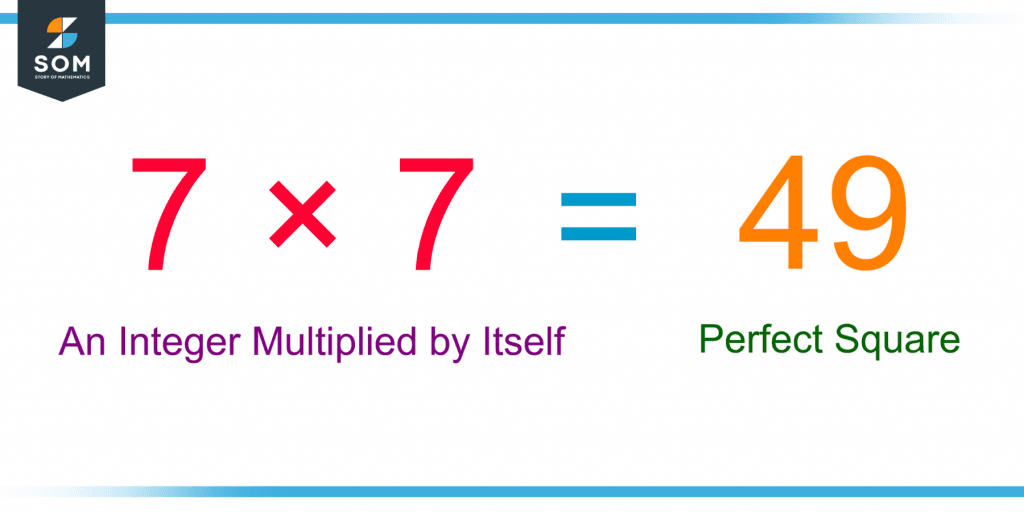
Figure 1 – A Perfect Square 49 Resulting from the Multiplication of an Integer 7 by Itself

Notation

Suppose an integer whole number m is multiplied by itself. Instead of writing it as m ✕ m, it is usually written as $m^2$. The exponent “2” is known as the “square,” and m² is pronounced as “m squared.” In figure 1, 7 $\boldsymbol\times$ 7 can also be written as 7².

Concept

The perfect square has the word “square” in it, which is somewhat related to the shape of the square.

The area is defined as the number of units in one column multiplied by the number of units in one row. A square has an equal number of units on all its sides.

A square with a side “p” length will have the area p $\boldsymbol\times$ p = p². If p units represent a perfect square, the units can be arranged in columns forming a square, with each side having the same number of units as the square root of p.

Figure 2 shows the illustration of a square with 5 points on each side. Counting the rows and columns or multiplying a row with a column will give the perfect square of 5, i.e., 25.

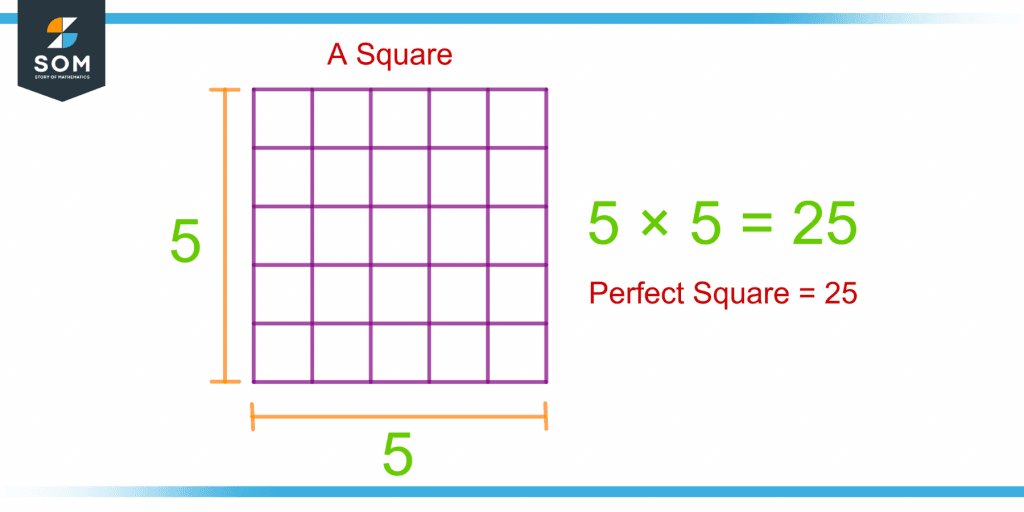
Figure 2 – Demonstration of a Perfect Square Through the “Square” Shape

So, an integer will be a perfect square if and only if its number of points can be arranged in a square.

Perfect Square – Always a Positive Number

A perfect square is always a non-negative number as its square root is an integer.

The product of a positive integer by itself gives a positive perfect square, and the product of a negative number by itself also gives a positive square number. This is because positive times positive is positive and negative times negative is also positive.

For example, the perfect square 81 can be achieved either by two products:

9 ✕ 9 = 81

(-9) ✕ (-9) = 81

Figure 3 shows the perfect squares of integers from 1 to 20.

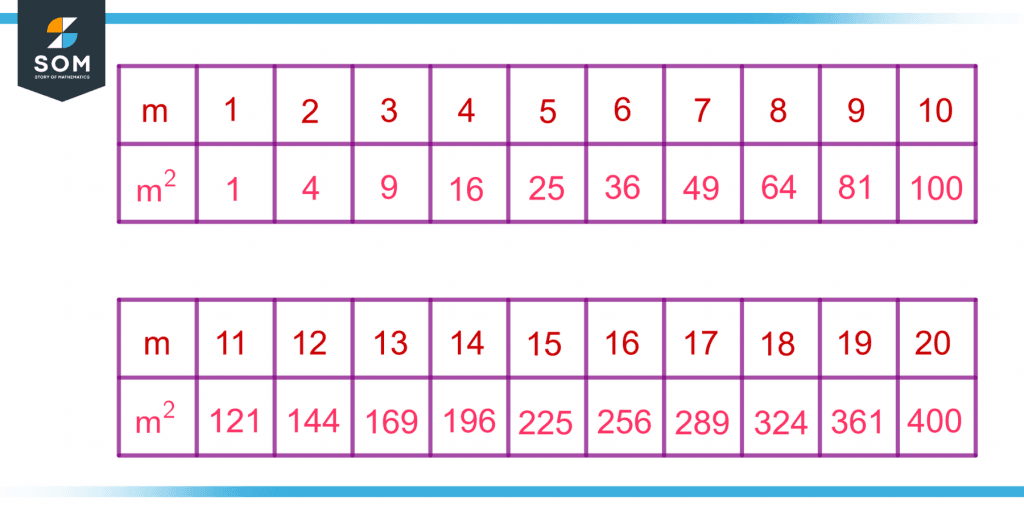
Figure 3 – Perfect Squares of Integers from One to Twenty

Square Root

The original integer can be obtained from the perfect square by taking the square root. For example, 441 is a perfect square. Its original integer can be found by taking its square root as follows:

$\sqrt{441}$ = 21

The square root of a number may be positive or negative. In the above example, square 441 can be obtained by taking the square of 21 or -21. But the radical symbol of the square root allows only the positive result.

Figure 4 shows how square and square root are inverses of each other.

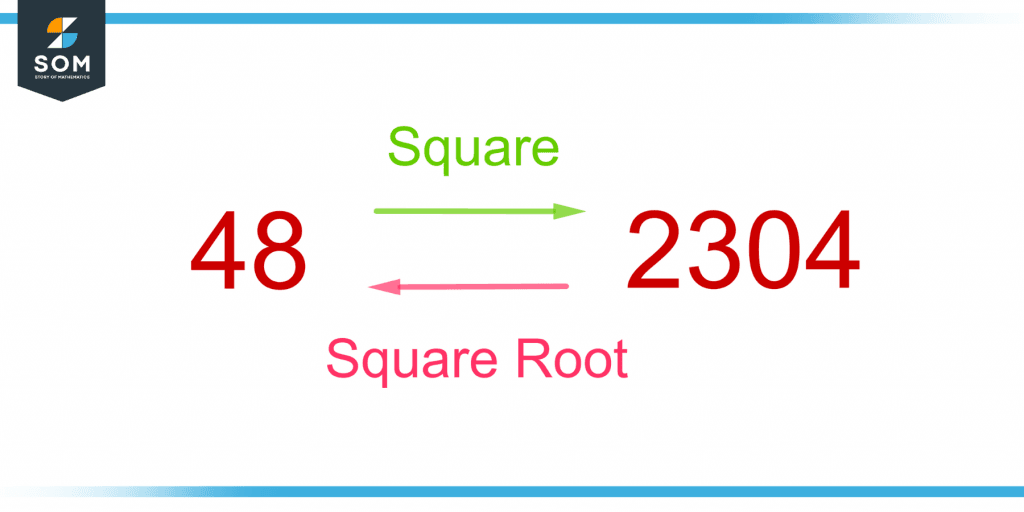
Figure 4 – Illustration of Square and Square Root as the Inverse of Each Other

Square Free Number

A square-free number is an integer that is not divisible by a perfect square except one. The factors of a square-free number are unique and different and don’t appear twice to make a perfect square. For example, the number 15 is square-free as it factorizes as follows:

15 = 3 ✕ 5

Whereas, the number 12 is not square-free as its factors include a perfect square:

12 = 3 ✕ 4

The perfect square is 4 which is equal to 2².

Perfect Square in Rational Numbers

A rational number can be written in the form of a/b, where a and b are integers. A perfect square of a rational number is a square of both the integers a and b. Also, the original rational number can be obtained by taking the square root.

For example, 121/100 is a perfect square of the rational number 11/10. It can be written as:

\[ \frac{121}{100} = \left( \frac{11}{10} \right)^2 \]

Perfect Square as a Summation

The perfect square m² can be written as a summation as follows:

\[ m^2 = \sum _{k=1}^{m}( 2k \ – \ 1) \]

The function (2k – 1) represents the function for odd numbers. So, the perfect square m² is equal to the sum of the first m odd numbers. For example, the perfect square 36 is equal to:

\[ 36 = 6^2 = \sum _{k=1}^{6}( 2k \ – \ 1 ) \]

Expanding the series gives the following result:

36 = 6² = 1 + 3 + 5 + 7 + 9 + 11

Recursive Formulas To Compute the Perfect Square

The following two recursive formulas are used to compute the perfect square m²:

m² = (m – 1)² + (2m – 1)

m² = 2(m – 1)² – (m – 2)² + 2

where m is the original number.

For example, if m = 3, m² can be calculated from the first recursive formula as follows:

3² = (3 – 1)² + [2(3) – 1]

3² = (2)² + [6 – 1]

3² = 4 + 5

3² = 9

The “Difference of Squares” Formula

The difference of square formula states that the product of the sum and difference of two numbers, c and d, will be equal to the difference of their squares. It can be written as:

(c + d)(c – d) = c² – d²

From this formula, the perfect square m² minus one is always equal to:

(m² – 1) = (m + 1)(m – 1)

For example, as we know that:

8² = 64

So:

(64 – 1) = 63 = (8 + 1)(8 – 1) = 9 ✕ 7

Perfect Squares in Trinomials

The following two formulas are used to identify a trinomial as a perfect square:

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

This means a trinomial will be a perfect square if and only if it factors out as (a + b)² or (a – b)².

For example, factorizing a trinomial (x² + 18x + 81) gives the factors as:

x² + 18x + 81 = (x)² + 2(x)(9) + (9)²

x² + 18x + 81 = (x + 9)²

Hence, this trinomial is a perfect square.

Example – Identifying the Perfect Square

Which of the two is a perfect square?

1035 or 1681

Solution

To know the perfect square, calculate the square root of both numbers:

$\sqrt{1035}$ = 32.17

$\sqrt{1681}$ = 41

As 32.17 is not a whole number, and 41 is a whole number, 1035 is not a perfect square, whereas 1681 is a perfect square.

All the images are created using GeoGebra.

Percentile Rank Definition < Glossary Index > Perimeter Definition