Power|Definition & Meaning

Power and exponents are used to represent the combination of a number being multiplied by itself a fixed number of times. They are mostly used to demonstrate a large quantity or a very small quantity in a form that is readable and writable for the user. 

For instance, we say that 3 raised to the power of 4 is equal to 3 multiplied by itself 4 times or 3 x 3 x 3 x 3. Instead of writing 3 several times, we can simply write it as 3⁴, where 3 represents the base number with 4 as the exponent. This combination of base and exponent is known as power.

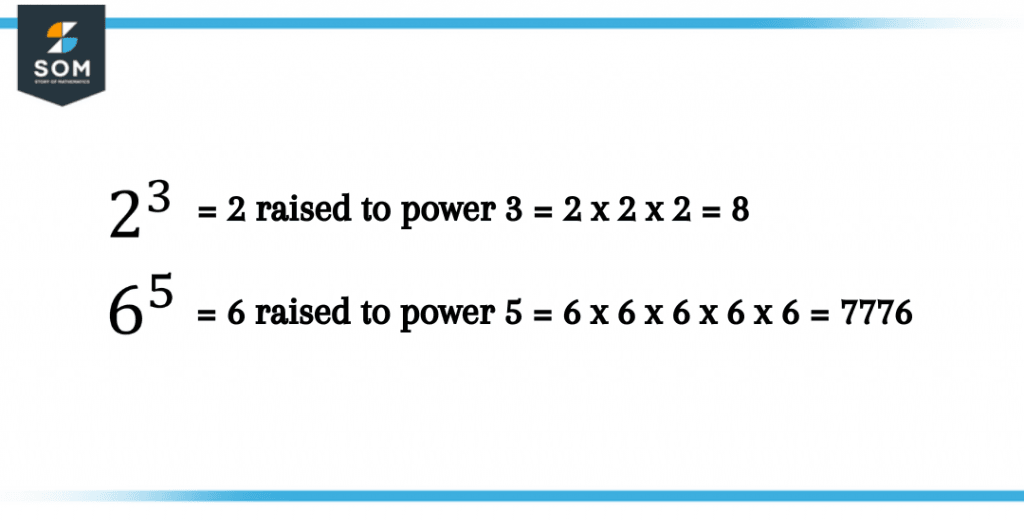
Figure 1 – Representation of the power of different numbers

3 raised to power 4 is a simple problem to cater to, but usually big numbers like a light year or the distance between the sun and earth and really minor values like the mass of an electron are represented in powers of 10. So rather than writing a bunch of zeros, we use power to simplify our problems.

The exponential number that is placed in the upper right corner of the base is known as a superscript.

What Is Power?

Power is a combination of two terms, a base, and an exponent. In mathematics, it refers to how many times a number is multiplied by itself. The base is the digit that is multiplied by itself. Whereas the exponent is the total number of times, the base has to be multiplied. In simple words, power is expressed in exponential form.

Furthermore, it denotes the repetition of a sequence of multiplication of a single number.

The most common power expression we have used is the quadratic equation, which holds terms having squared power. If the expression has an exponent of 3, it is referred to as cube powered. The higher powers are then related as ‘to the power of (x)’, where x is any integer.

Exponent

An exponent is a numeric digit representing the repetition of a number. It is usually denoted by the letter n. The generic form of power is Bⁿ, where B is the base with n as the exponent. For instance, if 8 is multiplied by itself, let’s say n times, then this means that:

8 x 8 x 8 x 8 x 8 x 8 x 8 x….. n = 8ⁿ

The verbal form of the above expression is 8 raised to the power of n. Thus indicating that exponents are just powers or occasionally known as indices.

The general form of exponents is given in the following figure.

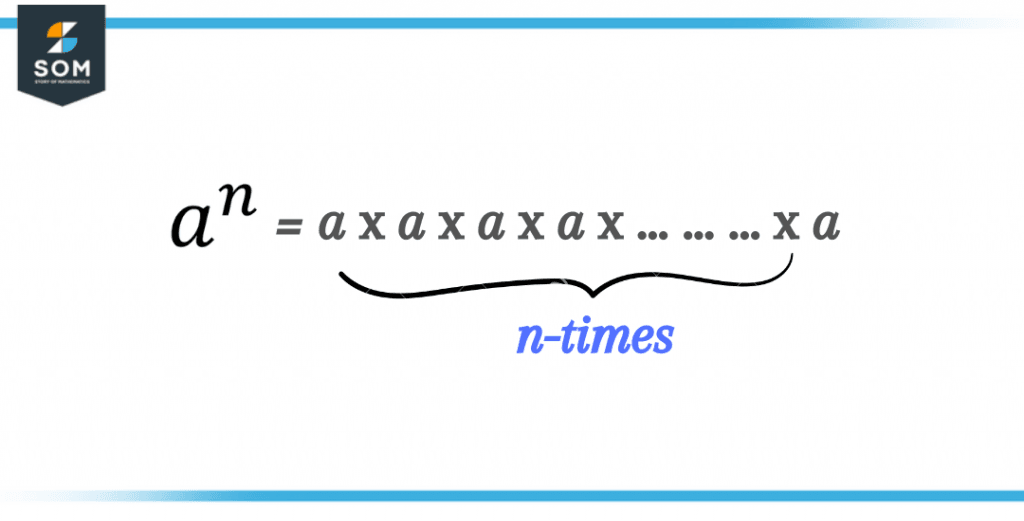
Figure 2 – General form of an exponent

Law of Powers

There are certain laws that help in simplifying expressions containing multiple power terms, or even a single term containing variable power. The laws are based on the arithmetic operations between the like and dislike bases and powers.

Multiplication Law

When there are two terms having the same base but different powers, and they are undergoing the arithmetic operation of multiplication then this law comes in handy. It says that if the bases are identical, then the powers can add up, such that:

a^m x aⁿ = a^m+n

Division Law

When there are two terms having the same base but different powers, and they are undergoing the arithmetic operation of division then this law comes in handy. It says that if the bases are identical, then the powers are subtracted, such that:

a^m / aⁿ = a^m-n

Exponential Law

When there is a term having a negative exponential and the term is in the numerator, then this law states that the whole term undergoes a reciprocal with the negative exponential converting into a positive exponential to the base:

a^-m = 1/a^m

Power Rules

We have gone through the different laws for solving power problems, but there are certain rules related to these laws which we are going to discuss in this topic. As of the moment, there are seven power rules which help us in identifying different word problems related to powers.

Product Rule

Let’s say we have two similar bases but their powers are different:

4³ x 4⁴

Then, we make use of the multiplication law and add those powers such that (3 + 4):

 4³ x 4⁴ = 4⁷

This means that 4 is multiplied by itself 7 times in a row:

4⁷ = 4 x 4 x 4 x 4 x 4 x 4 x 4 = 16,384

Suppose we have a more complex situation where:

4x³ x 2x⁴

Since the base here is x, we can add up the exponents and then multiply the coefficients of x:

4x³ x 2x⁴ = 8x⁷

Quotient Rule

Let’s say we have two similar bases but their powers are different in a fraction:

4⁶ / 4⁴

Then, we make use of the division law and subtract those powers such that (6 – 4):

 4⁶ x 4^-4 = 4^6-4 = 4²

This means that 4 is multiplied by itself 2 times in a row:

4² = 4 x 4 = 8

Suppose we have a more complex situation where:

4x² / 2x¹

Since the base here is x, we can add up the exponents and then multiply the coefficients of x:

4x² x 2x^-1 = 8x^2-1 = 8x

Power of Power Rule

Let’s say you encounter a situation where power is raised to some power of itself:

(x²)³

In such cases, simply multiply the powers together like normal integers:

x^2*3 = x⁶

We can break down this math:

(x²)³ = (x²) x (x²) x (x²)

(x²)³ = x.x.x.x.x.x

(x²)³ = x⁶

Power of Product Rule

Let’s say we have a base with two different variables having a single power outside the round brackets, such that:

(xy)³

Then, we make use of the distribution and multiplication law and distribute those powers such that:

(xy)³  = x³y³

This means that x and y are multiplied by themselves 3 times individually:

x³y³ = x.x.x.y.y.y

Suppose we have a more complex situation where:

(x²y²)³

Since there is power inside a power, we can multiply and distribute the exponents:

(x²y²)³  = x⁶y⁶

Power of Quotient Rule

Let’s say we have a base with two different variables in fractional form having a single power outside the round brackets, such that:

(x/y)³

Then, we make use of the distribution and division law and distribute those powers such that:

(x/y)³  = x³/y³

This means that x and y are multiplied by themselves 3 times individually:

x³/y³ = x.x.x./y.y.y

Suppose we have a more complex situation where:

(x²/y²)³

Since there is power inside a power, we can multiply and distribute the exponents:

(x²/y²)³  = x⁶/y⁶

Zero Rule

Anything raised to the power of zero, is 1, no matter how complex the equation is it will always be equated to 1.

(3².2⁵.9¹⁰⁰)⁰ = 1

Figure 3 – Zero power rule

Solved Example

Example 1

Simplify $\dfrac{x^4.y^5.z^8}{x^{-2}.y^2.z^3}$

Solution

Using the division rule to solve this problem:

= $\dfrac{x^4.y^5.z^8}{x^{-2}.y^2.z^3}$

= x^4-(-2).y^5-2.z^8-3

= x⁴⁺².y³.z⁵

= x⁶.y³.z⁵

This is the simplified form of the equation.

Example 2

Simplify 2ab + 4b (b² – 2a).

Solution

First, reduce the brackets:

= 2ab + 4b(b²) – 4b(2a)

= 2ab + 4(b¹⁺²) – 4b(2a)

= 2ab + 4b³ – 8ab

= 4b³ – 6ab

This is the final answer.

All images were created with GeoGebra.

Pound Definition < Glossary Index > Power Set Definition