JUMP TO TOPIC
Pound|Definition & Meaning
Definition
Pound, abbreviated as lb, is the unit of mass in the US and Imperial measurement systems. Its SI counterpart is the kilogram (kg), where 1 pound = 0.45359237 kg = 453.59237 grams. For example, a longsword weighs around 3 to 4 pounds.
What Is a Pound?
A pound is an imperial unit of estimating the mass of any object. It is a unit of measurement indicating the amount or quantity of matter occupied by any object. It tells us whether the thing being measured is heavy or light. It is abbreviated as ‘lb.’ A pound can also be called pound-mass (lbm). A pound is a unit of measurement in the imperial measuring system.

Figure 1 – Pound is the unit for measuring weight
Imperial Measuring System
The Imperial system is a system of measurement utilized in the United Kingdom and other Commonwealth countries. It includes units like feet, inches, ounces, pounds, gallons, etc. It is still often used to measure quantities like distance, weight, length, area, volume, etc., in the United Kingdom.
The imperial system is also known as the British imperial system because it was first defined in the British weights and measures act in 1824. This system came into official use in the British empire in 1826 and is still in use in some parts of the world.
Why Is the Pound Abbreviated as lb?
The word pound comes from ancient Rome, where they used the term libra pondo when referring to weight. The Latin words Libra meant weight, and pondo meant pound. The word pound is shortened from pondo, and the abbreviation lb is derived from the part of the word. This is how the word pound and its abbreviation came into existence.
What Is Pound Force?
It is defined as the gravitational force exerted on one pound of any mass on the surface of the earth. Pound force accelerates an object at the rate of 32.174 ft\s2. Figure 32.174 is the standard acceleration due to gravity on earth. Pound force is abbreviated as ‘lbf.’
Mass and Weight
As we are discussing the units of mass, we must take into consideration the difference between mass and weight and their units. Mass is the net amount of matter that a body has, whereas weight is the force of gravity acting upon an object by the earth.
In other words, mass is a quantity that doesn’t change and remains constant without due consideration to the location, but weight varies as we move from one place to another, i.e., the weight of any object on earth will be different as compared to the weight on mars, but the mass remains the same.
Pound mass is the unit of mass as it tells the amount of matter an object occupies. On the other hand, Pound force is the unit of weight as it includes the effect of gravitational force when being measured.
Conversion Between lbm and lbf
If we have the mass of an object in lbm, we can convert it into weight in lbf. There is a simple and easy method to convert mass into weight if we are given the mass and the force of gravity of that specific location.
First, we have to find the weight in lbm.ft\s2 by using Newton’s second law, i.e., f=ma. Next, we have to convert this weight into mass(lbm) by using the relationship 1lbm=32.174 ft\s2.
Let us consider an example to understand this conversion more efficiently.
Suppose the mass of an object is 38 lbm; estimate its weight on mars if the gravitational force on mars is 12.2 ft\s2.
Solving this example, we have mass in pounds and acceleration due to gravity. First, we use Newton’s second law to find the force of gravity in lbm.ft\s2.
mass = 38 pounds and acceleration due to gravity = 12.2 ft\s2
force=mass × acceleration due to gravity
f = 38 lbm × 12.2ft\s2
f = 463.6 lbm.ft\s2
Now, convert this value into lbf by using the relation:
1 lbm = 32.174 ft\s2
= 463.6 lbm.ft\s2 × 1\ 32.174ft\s2
= 463.6\32.174 lbf
= 14.4 lbf
Therefore, the object has a weight of 14.4 lbf on mars.
What Is an Ounce?
An ounce is a unit of measuring mass in the imperial system of measurements. Then what is the difference between pound and ounce? The difference is that if the object is heavy, its mass is measured in pounds, whereas the mass of lighter objects is measured in ounces.
It is just like grams and kilograms in the metric system, i.e., grams are used for lighter-weight objects, and a kilogram is used for heavier masses. An ounce is abbreviated as ‘oz.’ The relation between pound and ounce is shown below.
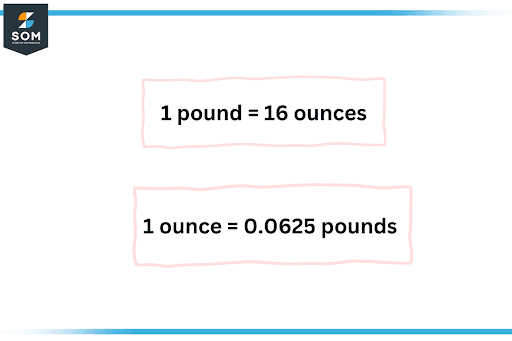
Figure 2 – Comparison between pound and an ounce
The Difference Between the Pound and Kilogram
Pound and kilogram are both units of mass, but a pound is an imperial unit of measuring mass, whereas a kilogram is a unit of mass in the metric system. The pound is derived from a Latin word, but kilogram is derived from a Greek word.
1 pound is equal to 0.453 kilograms which implies that a kilogram is 2.204 times a pound. A pound is abbreviated as lb, but a kilogram is abbreviated as kilo or kg.

Figure 3 – Comparison between pound and a kilo
Types of Pounds
There are many kinds of pounds that were in use in the past. Some of them are:
the Avoirdupois pound ( equal to 454 grams)
Troy pound ( equal to 373.241 grams)
Tower pound ( equal to 350 grams)
Merchant’s pound ( equal to 437 grams)
London pound ( equal to 467 grams)
The most typical of these pounds is the avoirdupois pound which is legally accepted as 454 grams and 0.453 kilograms. The remaining pounds were used for measuring different quantities in their respective time periods.
For example, the troy pound was used to measure jewelry, metals, ornaments, etc. Merchants’ pound, as the name indicates, was used for goods other than medicine, money, spices, etc. The London pound was used in different trading sites.
Solved Examples of Pound Conversion
Example 1
A person buys 30 kg of tomatoes for his vegetable shop. How many pounds did he buy?
Solution
We have mass in kilogram = 30 kg
To convert it into pounds, we use the relation:
1 kg = 2.204 pounds
Multiplying the mass in kg with 2.204:
30kg × 2.204 = 66.12 pounds
Hence, the person bought 66.12 pounds of tomatoes.
Example 2
Estimate the mass of an object in lbm if its weight on the moon is 7 lbf. Also, what will be its weight on earth?
Solution
We have the weight on the moon of an object = 7lbf.
First, we convert this weight into mass in lbm.ft\s2 .(remember that g=32.174ft\s2 for earth):
= 7 lbf * 32.174 lbm.ft\s2 \ 1 lbf
= 7 * 32.174 lbm.ft\s2
= 225.218 lbm.ft\s2
Next, we use newton’s second law to find mass:
m = f\a
(a=5.32ft\s2 for moon)
m = 225.218 lbm.ft\s2 \ 5.32ft\s2
m = 42.33 lbm
Hence, the mass of the object is 42.33 lbm.
Now, to find the weight of the object on earth where g=32.174 ft\s2, first we use newton’s second law to find the force of gravity in lbm.ft\s2:
F =ma
= 42.33 lbm * 32.174 ft\s2
= 1361.9 lbm.ft\s2
Now converting this value into lbf:
= 1361.9 lbm.ft\s2 *(1 lbf \ 32.174 lbm.ft\s2)
= 1361.9 \ 32.174 lbf
= 42.32 lbf
Therefore, the weight of the object on earth is 42.32 lbf.
All images are created using GeoGebra.
