Position|Definition & Meaning

A thing’s position can be defined as the amount of space it takes up in relation to other things. In order to describe the location of one thing in relation to another, we can use phrases such as “in front,” “behind,” “left,” “right,” “above,” “below,” “top,” and “bottom,” among others. 

In the following figure, the position of a parallelogram is right to the circle.

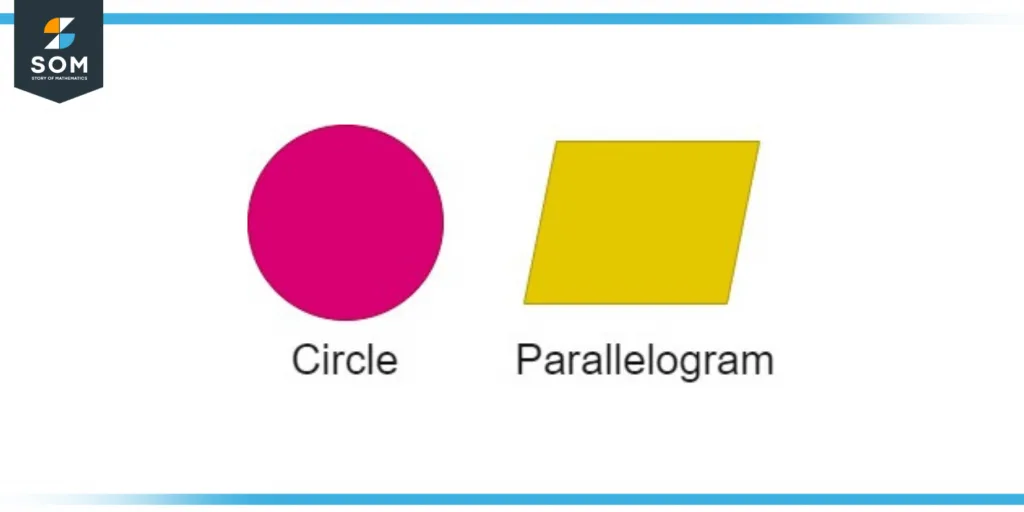
Figure 1 – Position of a parallelogram

In the Context of Mathematics, What Do “Position” and “Movement” Mean?

In the context of mathematics, “position” refers to the process of determining and noting where something is situated, typically on a grid or a map. In most cases, your youngster will complete this task using coordinates. The ideas of rotation, translation, and symmetry are included under the umbrella term “movement.”

In geometry, sometimes known as the study of shapes, issues such as movement and position are both covered.

Figure 2 – Position of the rounded rectangle

What Exactly Is a Coordinate?

The location of such a point on such a grid can be determined with the help of something called coordinates. A coordinate is indeed a pair of numbers that are distinguished by a comma and enclosed in brackets.

For example, a coordinate would look like this: (7, 8). The numbers that make up a coordinate provide you with information about how far you need to travel along either axis of a grid in order to locate the point.

By telling yourself to move “all along the corridor but also up the stairs,” you can help yourself remember that you should first move all along the bottom axis (X) to find the very first number of a coordinate and then start moving up the axis (Y) to find the 2nd number of a coordinate.

You can do this by using the phrase “all along the corridor but also up the stairs.” To locate the point indicated by the coordinates (4, 2), move four spaces down the axis that runs horizontally across the bottom of the grid, and afterward, move two spaces vertically along the axis that runs horizontally across the top of the grid.

What Exactly Do the Terms “Rotation,” “Translation,” and “Symmetry” Mean?

The technique of spinning as well as turning a form, is referred to as rotation. The form rotates 360 degrees while maintaining its appearance and size during the process.

Moving a shape along a grid either up, down, left, or right is called translation. The shape does not rotate or alter its outward appearance or its size; rather, it merely moves in one or even more directions.

Reflection is the key to understanding symmetry. If you are able to draw a line across the middle of a shape and each half is indeed a mirror image to the other, then the shape is said to have symmetry.

What Is the Definition of a Position in Terms of a Vector?

A position vector is indeed a straight line that is used to define the location of a moving point in relation to a body. One end of the line is attached to the body, while the other end of the line is attached to the moving point. When the point moves, its position vector will undergo a change in either its length, its direction, or both, depending on the nature of the movement.

It is possible to define a position vector as a vector that represents either the position or even the location of a particular point with respect to an arbitrary reference point such as the origin. Always moving in the direction of a certain location, the direction of a position vector points in the direction of a vector’s origin.

Vectors and Scalars Are Two Different Types of Mathematical Quantities

When determining position, the direction that one faces is quite essential. When you claim that you are located at positive 6 meters in the x-direction, what you are actually indicating is that you are located 3 meters towards the right of a y-axis. This points in a certain direction.

A number that takes into account direction is referred to as a vector. A scalar is a number that may be written in either direction without affecting its value.

Scalars include things like temperature, for instance. Because there is no clear path that it follows. Even if it may be 70 degrees Fahrenheit outside, the temperature inside the building is not 70 degrees Fahrenheit. It could be 40 degrees Celsius, but it will never be 40 degrees Celsius when you head west. Not at all how things work with temperature. The temperature is an example of a scalar.

Because the direction is important, the position is represented as a vector. However, distance is indeed a scalar variable. The length of your journey can be measured in distance. For instance, if you sprint around your room while keeping the axis on the ground, you might run a fairly long way, all the way up to a total distance of fifty meters.

However, your location is not fifty meters away. For example, your position could be described as having a minus 3-meter value just on the x-axis and a plus 4-meter value on the y-axis. The distance you traveled did not change regardless of the direction in which you ran; you still covered fifty meters.

Therefore, while considering the distance, orientation is irrelevant. The measure of distance is indeed a scalar.

Illustration of a Position by Vector

In most situations, a position vector of such an item is calculated by starting from the origin. Imagine that an item is placed within space in the following manner.

The Formula for Positioning Using a Vector

Before we can calculate a position vector of any point in the xy plane, we need to have the point’s coordinates in front of us.

Take into consideration points A and B, each of which has the coordinates (w1, x1) and (w2, x2), accordingly. In order to calculate a position vector, we must first take the respective components of A and subtract them from the components of B in the following manner:

AB = (w2 – w1)*i + (x2 – x1)*j

Point A serves as the starting point for the position vector AB, which continues on to point B.

A Numerical Example of Position

Which of these figures lies beneath the Circle?

Figure 3 – Position representation

Solution

From the previous knowledge of position, the triangle is beneath the circle.

All mathematical drawings and images were created with GeoGebra.

Population Definition < Glossary Index > Pound Definition