Proof|Definition & Meaning

Figure 1 shows the proof for the statement: “If two angles are linear pairs, then they are supplementary angles.” 

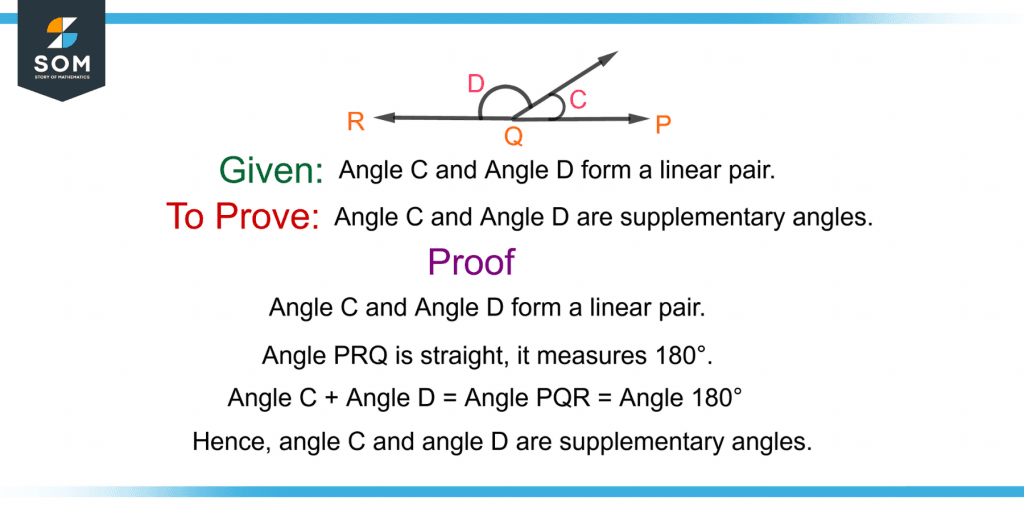
Figure 1 – An Example of Proof that a Linear Pair forms Two Supplementary Angles

History

The word “proof” is derived from the Latin word “probare,” meaning “to test.” It also has its origin in the Spanish word “probar,” the Italian word “provare,” and the German word “probieren,” which all means “to try.”

The idea and demonstration of mathematical proof were first presented in ancient Greek mathematics. Thales and Hippocrates gave the first proofs of the fundamental theorems in geometry.

The axiomatic method given by Euclid revolutionized mathematical proof. The procedure starts with axioms, undefined terms, and propositions self-evidently assumed true and proved using deductive logic.

Purpose

The purpose of formulating proof is to convince an audience of the truth of a statement. Many rigorous arguments are made to prove the authenticity of the statement.

There are many ways to present proof through different premises. A vague or incomplete argument does not gain acceptance of the proof.

Mathematical Logic

The field of mathematical logic forms the basis for the concept of proof. It studies formal mathematical logic with sub-areas such as set theory, proof theory, and model theory.

Proof Theory

The proof theory involves mathematical techniques to analyze proofs represented as mathematical objects. Proofs are presented as data structures such as boxed lists, lists, and trees which are inductively defined and constructed according to rules of inference and axioms.

The proof theory includes ordinal analysis, reverse mathematics, structural proof theory, provability logic, automated theorem proving, proof complexity, and proof mining.

Conjecture

A conjecture is a tentative statement or proposition made without any proof. It is an idea observed when viewing a similar pattern that holds for many different cases. It is a conclusion that is not rigorously proved.

A conjecture can also be called a “hypothesis,” but it is not written in a testable or formal way. An example of a conjecture is Riemen’s Hypothesis which paved the way for many areas of mathematics to prove them.

Axiom

An axiom is a statement that is considered to be true to establish it as a starting point for further arguments and reasoning. It is also known as an assumption or postulate. It is derived from the Greek word “axioma,” which means “something that is considered worthy or fit” or “something that proposes itself as evident.”

For example, the symmetric axiom states that if x = z, then z = x, also known as the axiom of equality.

Theorem

A theorem is a statement that has already been proved through deductive logic arguments. It is a conjecture that has been verified using axioms to start logical reasoning and is accepted worldwide. An example of a theorem is Fermat’s Last Theorem which Andrew Wiles proved in 1995.

Types of Proof

There are various methods to prove a statement which are given as follows:

Direct Proof

In direct proof, a statement is proved by logically using mathematical definitions, axioms, and known theorems. Figure 2 shows the direct proof that the sum of two odd integers is always an even integer.

Figure 2 – The Direct Proof of the Sum of Two Odd Integers is an Even Integer

Proof by Contradiction

In proof by contradiction, a statement opposite to the original statement is proved. In the proof, a contradiction proves the opposing statement to be false, thereby proving the original statement true.

For example, to prove by contradiction that if (m³ + 5) is odd, then m is even for all integers, it is assumed that m is odd, which negates the given proposition. Figure 3 shows its proof by using the contradiction method.

Figure 3 – An Example of Proof by Contradiction

The last equation in figure 3 is impossible (contradiction) as 5/2 (rational number) is not an integer, whereas the right-hand side results in an integer under the closure property w.r.t addition. Therefore the assumption that m is odd must be false for (m³ + 5) to be odd. Hence, m must be even.

Proof by Contraposition

Proof by contraposition refers to proving the contrapositive statement “if not y, then not x,” which proves the original statement “if x, then y.”

For example, to prove the statement “if a² is even, then the integer a is even” by contraposition means proving the equivalent assumption “if a is not even, then a² is not even.”

Suppose a is not even, then it is odd. By definition, the product of two odd integers is odd, so a.a = a² is odd, which means a² is not even. Hence, by contraposition, it is proved that if  a² is even, then a is even.

Proof by Induction

Proof by induction requires proving a base case by inductive arguments. If the base case P(n) and the following case, e.g., P(n + 1), is provable, then the other infinite cases are also provable. For example, to prove by induction that the positive integer (2j – 1) represents an odd number, consider figure 4.

Figure 4 – An Example of Proof by Induction

Example

Prove that the sum of any two consecutive numbers is an odd number using direct proof, proof by contradiction, and contraposition.

Solution

Direct Proof

Assume g and h are two consecutive integers, so by definition of consecutive numbers:

h = g + 1

Adding g and h and placing the value of h in the equation gives:

g + h = g + (g + 1)

g + h = 2g + 1

As (2g + 1) represents an odd number, hence the sum of two consecutive integers is an odd number.

Proof by Contradiction

Assume g and h are consecutive integers and the sum of g and h is not odd. If (g + h) is not odd, then there exists no integer l such that:

g + h = 2l + 1

But as g and h are consecutive, then:

g + h = g + (g + 1) = 2g + 1

Hence, there is a contradiction between (g + h) = 2l + 1 since there exists no integer l and (g + h) = 2g + 1 as the integer g exists, so:

g + h ≠ 2l + 1

Hence, the assumption that the sum of g and h is not odd must be false, so it is proved by contradiction that the sum of two consecutive numbers is odd.

Proof by Contraposition

The contrapositive statement will be if the sum of g and h is not odd, then g and h are not consecutive integers. If (g + h) is not odd, then there does not exist an integer w such that:

g + h = 2w + 1

So, g + h = a + (a + 1) does not hold for any integer a. But since (a + 1) is the successor of a, it implies that g and h cannot be consecutive. Hence, the contrapositive statement is proved, ultimately proving the original statement.

All the images are created using GeoGebra.

Profit Definition < Glossary Index > Proper Factor Definition