Proper Factor|Definition & Meaning

Factorization is a common procedure used in algebra and other forms of mathematics. Any integer can be factorized into multiple factors. These factors have different properties. One type of factors is a proper factor. They are such factors that are not equal to 1 or the original number that was taken as an input to the factorization process. 

The following figure illustrates an example of a proper factor that has been iterated in the definition:

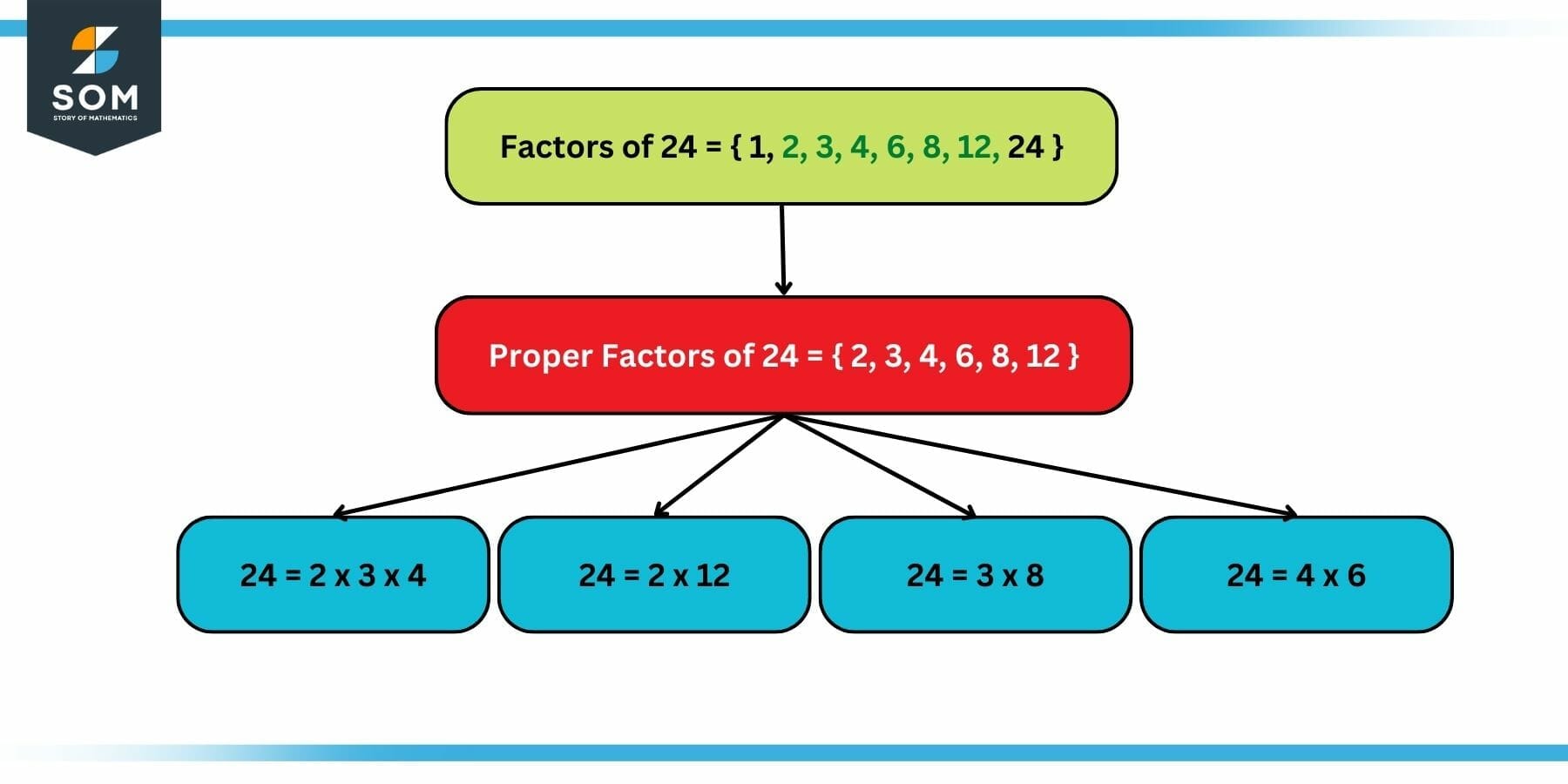
Figure 1: Example of Proper Factor

What Is Factorization and Proper Factor?

To understand the process of factorization, we need to understand what factors are. So let us see that in a bit more detail.

Factor

Factors are constituent parts of an integer such that the original integer can be obtained by multiplying the factors together. For example, the factors of 6 are 2 and 3. If we multiply 2 and 3, we obtain 2×3 = 6, which proves that 2 and 3 are the factors of 6 indeed. If you divide a number by its factor, the remainder is zero.

Proper Factor

A proper factor, also known as a proper divisor in mathematics, is a factor of a number that is greater than one and less than the number itself that evenly divides the given number, leaving zero as a remainder. For example, let us say that we want to find the factors of the number 10.

Now let us assume for the moment that we know how to find these factors, and we find out that 10 can be factorized into 1, 2, 5, and 10. Since 1 and 10 are not valuable, we say that 2 and 5 are the proper factors of 10.

For all integers, two factors are always there from the definition of factors. One of the factors is 1, and the other one is the number itself. From the definition of factors stated above, we can see that these numbers are actually termed factors, but they do not really add value to our cause mathematically.

For example, if we say that 1 and 24 are the factors of 24, I have just reiterated an obvious fact, and this information is useless. So, the proper factor is a type of factor that is not 1 or the original number.

Proper factors are a fundamental concept in mathematics, playing a key role in various areas of mathematics, including number theory, algebra, geometry, and trigonometry. Understanding and using proper factors effectively is essential for solving mathematical problems and making further advances in mathematics.

Factorization

Factorization is the name for the process of finding the factors of an integer. Continuing from the previous example, we know that 2 and 3 are factors of 6. But how did we arrive at these factors? How would I find these factors for a complex or difficult integer? To solve these problems, we need to understand the factorization method.

Method of Finding Proper Factors

Let us simplify the process into steps. Let us say that we are asked to find the factors of an integer X. First we will create a set of integers from 1 to X.

Second, we will divide X by all these integers one by one. After every division, we will check whether the remainder of the division is zero or not. If the remainder is zero, then we store the dividing number or the divisor into another set since it’s a factor by definition.0

By the end of this process, we end up with a set of factors. Now to find the proper factors, we would drop 1 and the original integer and thus obtain the set of proper fractions. The step-wise summary is given below:

Figure 2: Process of Finding Proper Factors

Step 1: Define the set of all potential factors smaller than the given number excluding 1.

Step 2: Divide the given number by all potential factors one by one and note the remainder.

Step 3: Filter out the integers that have zero remainders.

Example of Finding Proper Factors

Let us consider an example. Suppose we need to find the factors of the number 14. Now here are the steps:

(a) We define the set of all integers smaller than 14, excluding 1, which is given below:

Potential Factors = { 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 }

(b) Now we divide 14 by all these numbers one by one and note the remainder set given below:

Remainders = { 0, 2, 2, 4, 2, 0, 6, 5, 4, 3, 2, 1 }

(c) Now we filter out the integers that have zero remainders given below:

Proper Factors = { 2, 7 }

Hence, 2 and 7 are the proper factors of the number 14.

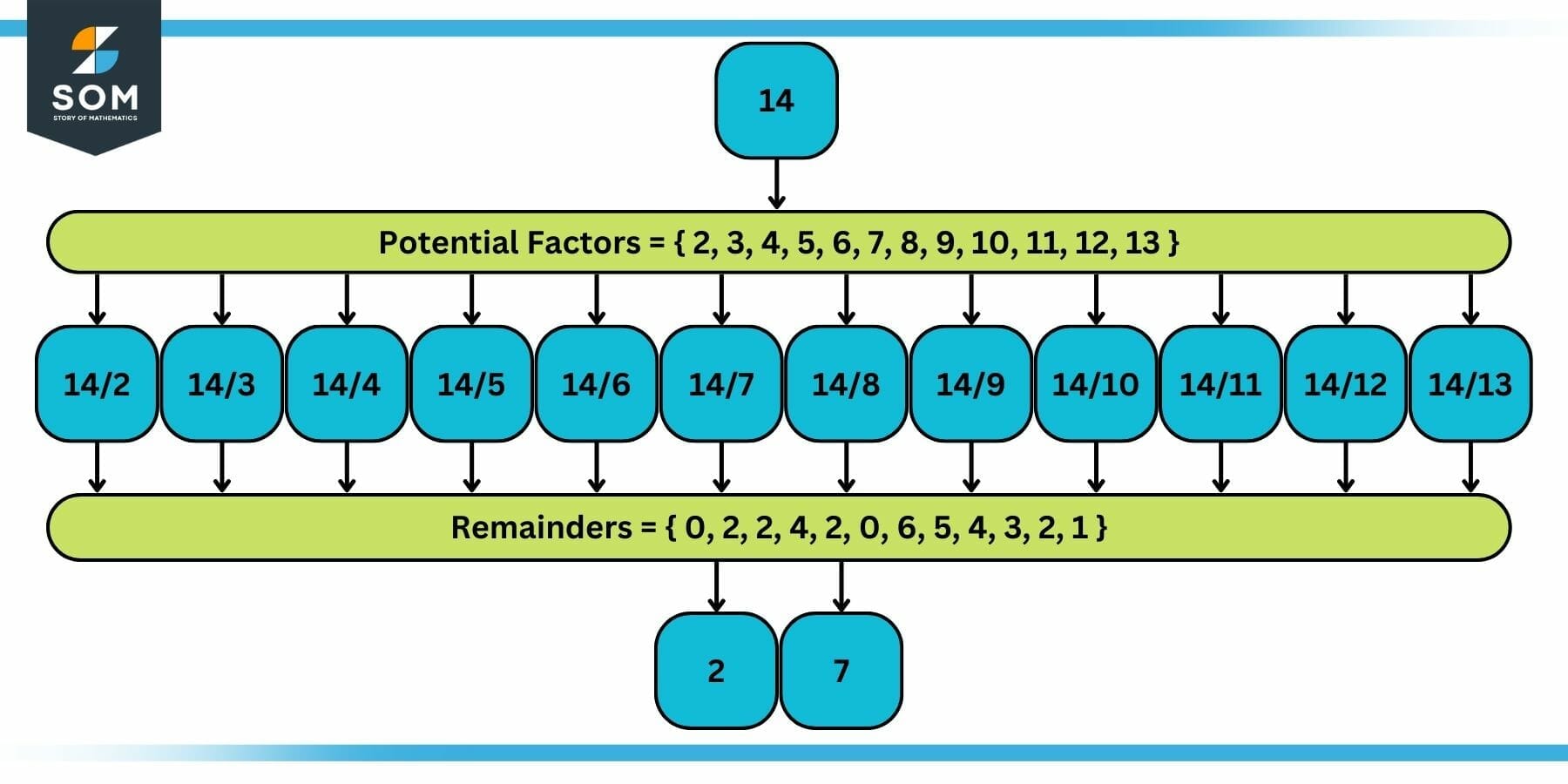
Figure 3: Example of Finding Proper Factors

Applications of Proper Factors

Proper factors are used in various mathematical concepts and applications, but for the sake of this article, let us consider the following four:

1. Finding the greatest common divisor (GCD).
2. Determining the prime factorization of a number.
3. Solving problems in number theory.
4. Solving problems in geometry and trigonometry.

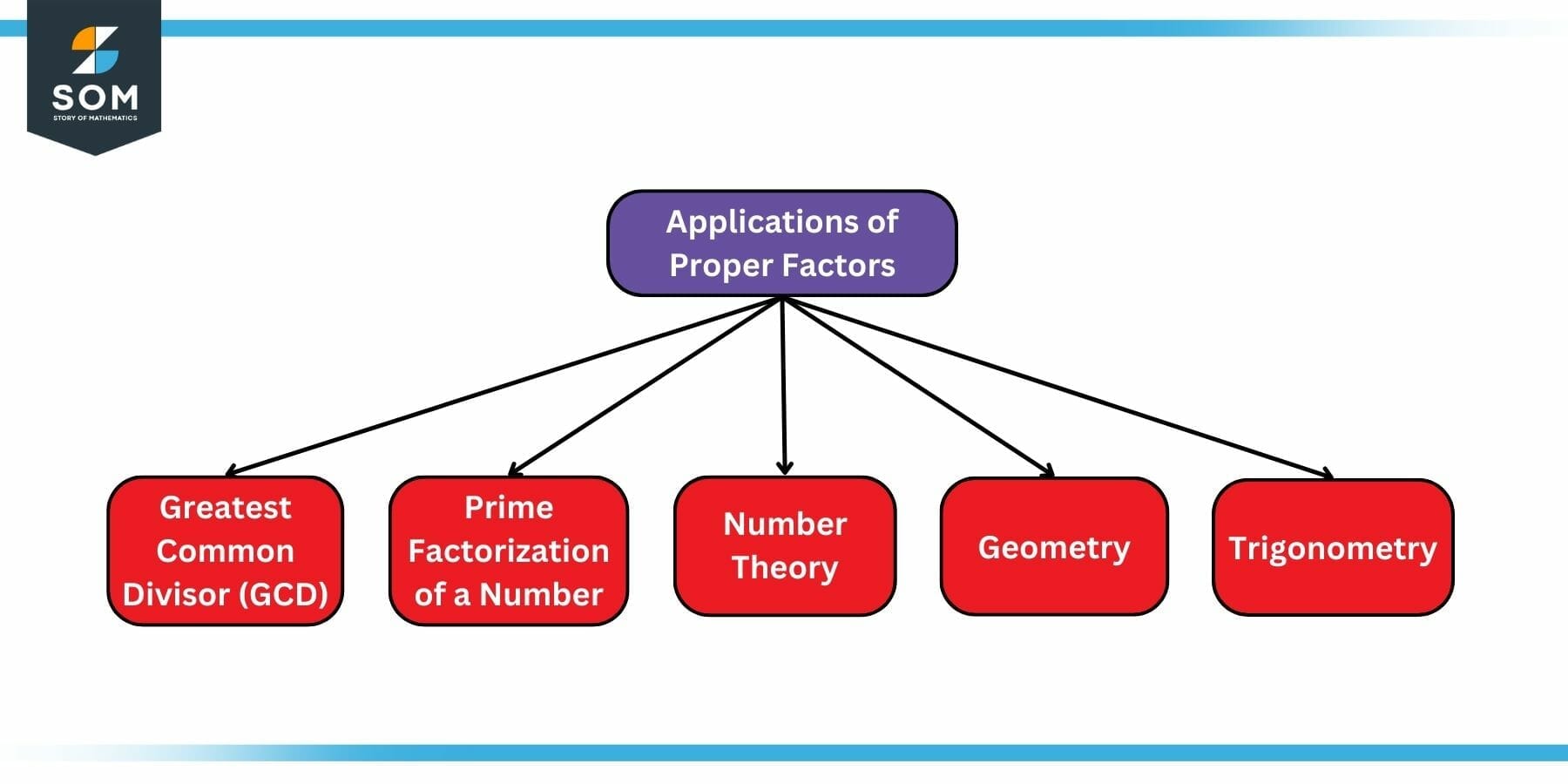
Figure 4: Applications of Proper Factors

Let us explain them one by one.

1. Finding the Greatest Common Divisor (GCD)

The greatest common divisor (also called the highest or greatest common factor) of two or more numbers is the largest shared factor between all of them. To find the greatest common divisor, one can list the proper factors of each number and then find the largest one that is common to all of them.

For example, the proper factors of 18 are 2, 3, 6, and 9, and the proper factors of 24 are 2, 3, 4, 6, 8, 12. As another example, the greatest common divisor of 24 and 18 is 6.

2. Determining the Prime Factorization of a Number

Another important use of proper factors is in finding the prime factorization of a number. The method of finding the prime factors of a given number that multiply together to form that number is called prime factorization. For example, the prime factorization of 24 is 2 x 2 x 2 x 3.

The prime numbers are the only proper factors of a number that are also prime numbers, making it easier to perform mathematical operations with the number.

3. Solving Problems in Number Theory

In number theory, proper factors play a role in understanding divisibility and the distribution of primes. For example, it is known that the quantity of proper factors of a number is directly related to whether the number is prime or composite.

A prime number has only two factors, i.e., 1 and itself, whereas a composite number has more than two factors. This means that the prime numbers have no proper factors. This observation has been used to develop algorithms for finding prime numbers and to understand the distribution of primes in the number system.

4. Solving Problems in Geometry and Trigonometry

Proper factors are also used in solving problems in geometry and trigonometry, such as finding the sides of a right triangle when given the area and one side length. In such problems, proper factors can be used to simplify expressions and to determine the necessary conditions for a solution to exist.

Numerical Problems of Proper Factors

Example 1

Calculate the proper factors of the number 8.

Solution

(a) We define the set of all integers smaller than 8, excluding 1, which is given below:

Potential Factors = { 2, 3, 4, 5, 6, 7 }

(b) Now we divide 8 by all these numbers one by one and note the remainder set given below:

Remainders = { 0, 2, 0, 3, 2, 1 }

(c) Now we filter out the integers that have zero remainders given below:

Proper Factors = { 2, 4 }

Hence, 2 and 4 are the proper factors of the number 8.

Example 2

Show that the number 11 is a prime number.

Solution

(a) We define the set of all integers smaller than 11, excluding 1, which is given below:

Potential Factors = { 2, 3, 4, 5, 6, 7, 8, 9, 10 }

(b) Now we divide 11 by all these numbers one by one and note the remainder set given below:

Remainders = { 1, 2, 3, 1, 5, 4, 3, 2, 1 }

(c) Now we filter out the integers that have zero remainders given below:

Proper Factors = { }

This means that the number 11 has no proper factors. It is only divisible by 1 and itself. So it’s a prime number.

All images were created with GeoGebra.

Proof Definition < Glossary Index > Proper Fraction Definition