Proper Fraction|Definition & Meaning

What Is a Proper Fraction? 

If a fraction’s numerator is lower than that fraction’s denominator, then we refer to that fraction as a proper fraction. A correct fraction’s value is guaranteed to be less than one at all times.

For illustration, Sami bought a bar of chocolate and cut it into quarters so that each portion was the same size. He kept one portion for himself and handed Rachel the remaining four portions. The fraction used to represent Sam’s share is one-fourth, and Rachel’s share is three-quarters. Because the numerator in each fraction is less than the denominator, we refer to these fractions as correct fractions.

The term “proper fraction” refers to a fraction in which we can say that value of the numerator is always lower than the value of the denominator.

For instance, the fractions 18/25, 17/45, 64/78, 1/4, and 1/9 are all correct. The numerator and the denominator are the components that make up a fraction; the different types of fractions can be distinguished by examining the relationship between these two values.

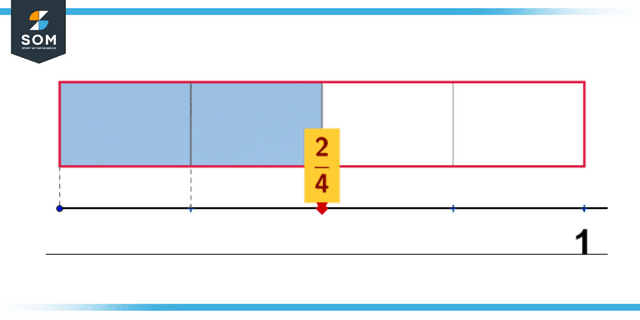
Figure 1: Representation of proper fraction.

Addition of Proper Fraction

When adding two appropriate fractions, we start by adding the numerators if the fractions supplied are like fractions, which means that the denominators are identical in both fractions. For instance, adding 2/8 and 3/8 is simply adding the numerators because the fraction’s denominators remain unchanged. 5/8 will be the total after adding together 2/8 and 3/8.

To add proper fractions that are not equivalent, however, we must first determine the Least Common Multiple (LCM) of the denominators and then reinterpret the fractions as equivalent fractions by using the LCM as the common denominator. This allows us to add proper fractions that have different denominators.

Now that all of the denominators have converged on a single value, we may combine the numerators and then write the sum of those numerators as the ultimate numerator on top of the denominator that they share in common.

To add 2/3 and 4/5, we must first determine the least common multiple of the denominators. Fifteen is the LCM of 3 and 5. Now that we have both fractions, we multiply each one by the accurate count (in this case, 5 and 3, respectively) to make the denominators equal. This results in 22/15, equal to (10 + 12)/15.

Subtracting Proper Fraction

Deducting correct fractions from a whole number is quite similar to adding them. To determine the difference between two proper fractions with the same denominator but different numerators, we need to determine the difference in the fractions’ numerators while maintaining the original denominator. For instance, the difference between 6/9 and 4/9 will be 2/9.

Now, we want to subtract proper fractions that are unlike one another, in which the denominators are different. In that case, we will take the Least Common Multiple (LCM) of the denominators and reinterpret the fractions as equivalent fractions by using LCM as the common denominator.

This will allow us to subtract the proper fractions that are unlike one another. After ensuring that all of the denominators are identical, we subtract the numerators and mark the outcome on the denominator they share.

To subtract 8/9 from 3/4, we must first determine the least common multiple of the denominators. The lowest common multiple of 9 and 4 is 36. Now that we have both fractions, we multiply each one by such a number (in this case, 4 and 9 correspondingly) to make the denominators equal. This yields 5/36, which equals (32 – 27)/36.

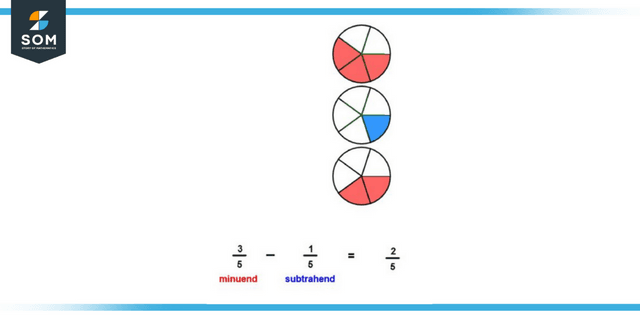
Figure 2: Representation of subtraction of proper fraction.

Multiplication of Proper Fraction

Multiplication and division of appropriate fractions are more accessible in a sense, in contrast to the addition and subtraction of proper fractions. We first multiply the numerators provided, then multiply the denominators, and finally, we decrease or simplify the fraction that has been produced.

To multiply 2/6 by 5/4, for instance, we first multiply the numerators 2 and 5, which gives us the number 10, and then multiply the denominators 6 and 4, which gives us the number 24. The product is listed as 10/24, although this number can be lowered to 5/12 if necessary.

Division of Proper Fraction

The process of dividing appropriate fractions is analogous to the process of multiplying. The only difference is that we switch the sign for division to the sign for multiplication and then multiply the first fraction by the inverse of the second fraction, which is called the reciprocal.

For instance, now let’s divide: 4/9 ÷ 2/3. This will result in 12/18 when 4/9 is multiplied by 3/2. This can be decreased even further to two-thirds.

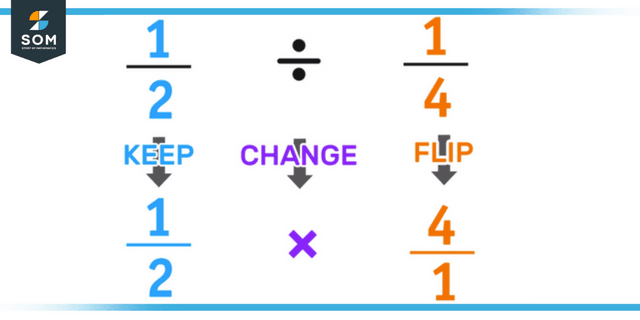
Figure 3: Representation of division of proper fraction.

Changing Improper Fractions Into Proper Fractions

In mathematics, it is possible to change an improper fraction into a mixed fraction, which is the product of combining a whole integer with a proper fraction. For illustration purposes, let us transform the improper fraction 13/5 into a mixed fraction by following the methods outlined below:

• To get the fraction’s answer, divide the numerator by the denominator. When we divide 13 by 7, we get 1 as the quotient and 6 as the remainder in this particular situation.
• The derived quotient should be written as a whole integer, and the remainder should be written as the numerator with the same denominator. In this situation, the absolute number will be the quotient (1), the remainder (6) will become the new numerator, and the denominator will remain the same.

Proper and Improper Fractions

By comparing the values of the numerator and the denominator, we can determine which of the two fractions is a proper fraction and which of the fractions is an improper fraction. If we take the reciprocal of a proper fraction, such as 5/7, we get an improper fraction. On the other hand, 5/7 is an example of a proper fraction.

Examples of Proper Fractions

Example 1

What do we get if we add the following proper fraction?

2/11 + 3/11 + 4/11 = ?

Solution

The denominator of all three fractions is the same (11), so we can simply add the numerators:

numerator = 2 + 3 + 4 = 9

The denominator of the result is the common denominator itself, so 11. Therefore:

2/11 + 3/11 + 4/11 = 9/11

Example 2

What do we get if we subtract the following proper fraction?

2/5 – 1/5 = ?

Solution

Since the denominator is common (5), we can simply subtract the numerators:

numerator = 2 – 1 = 1

Now, we can just write the common denominator below it to get the resulting fraction, so:

2/5 – 1/5 = 1/5

All images/graphs are created using GeoGebra.

Proper Factor Definition < Glossary Index > Property Definition