JUMP TO TOPIC
Property|Definition & Meaning
Definition
Defining characteristics or qualities that allow us to identify a particular thing and distinguish it from others. For example, symmetry and dimensionality. A circle is perfectly symmetrical around any line passing through its center, while a trapezium has no line of symmetry. Similarly, a circle is a two-dimensional shape, whereas a sphere is three-dimensional (has depth).
A property of an object refers to a characteristic or attribute that describes or defines the object. It can be a physical property such as size, shape, color, or texture, or it can be a functional property such as weight, capacity, or electrical conductivity.
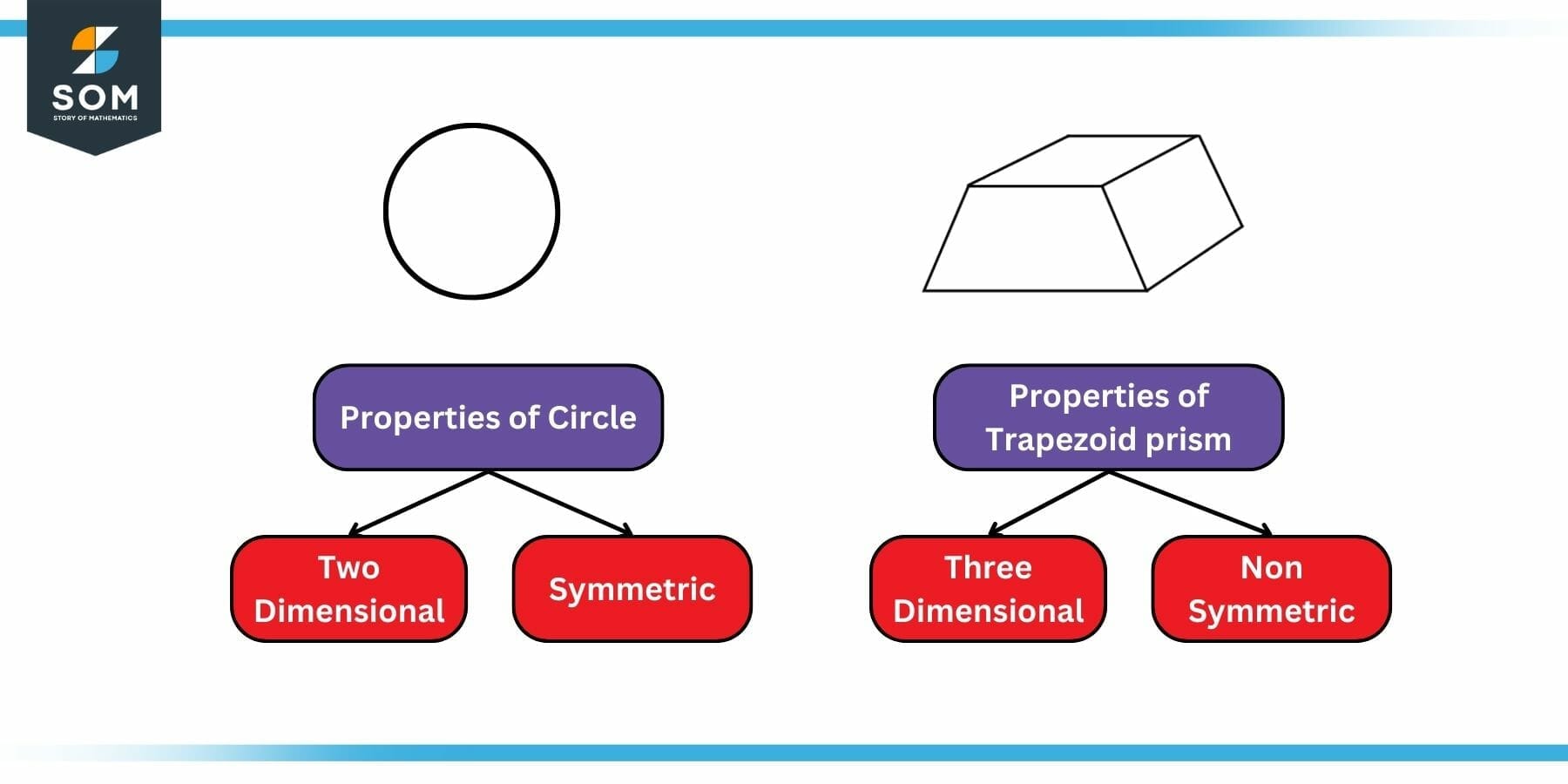
Figure 1: Example of Property
Mathematical Property
A property can also be a mathematical property, such as symmetry, associativity, or distributive, which can be used to describe and define mathematical objects. The properties of an object are used to distinguish it from other objects and to describe its unique characteristics.
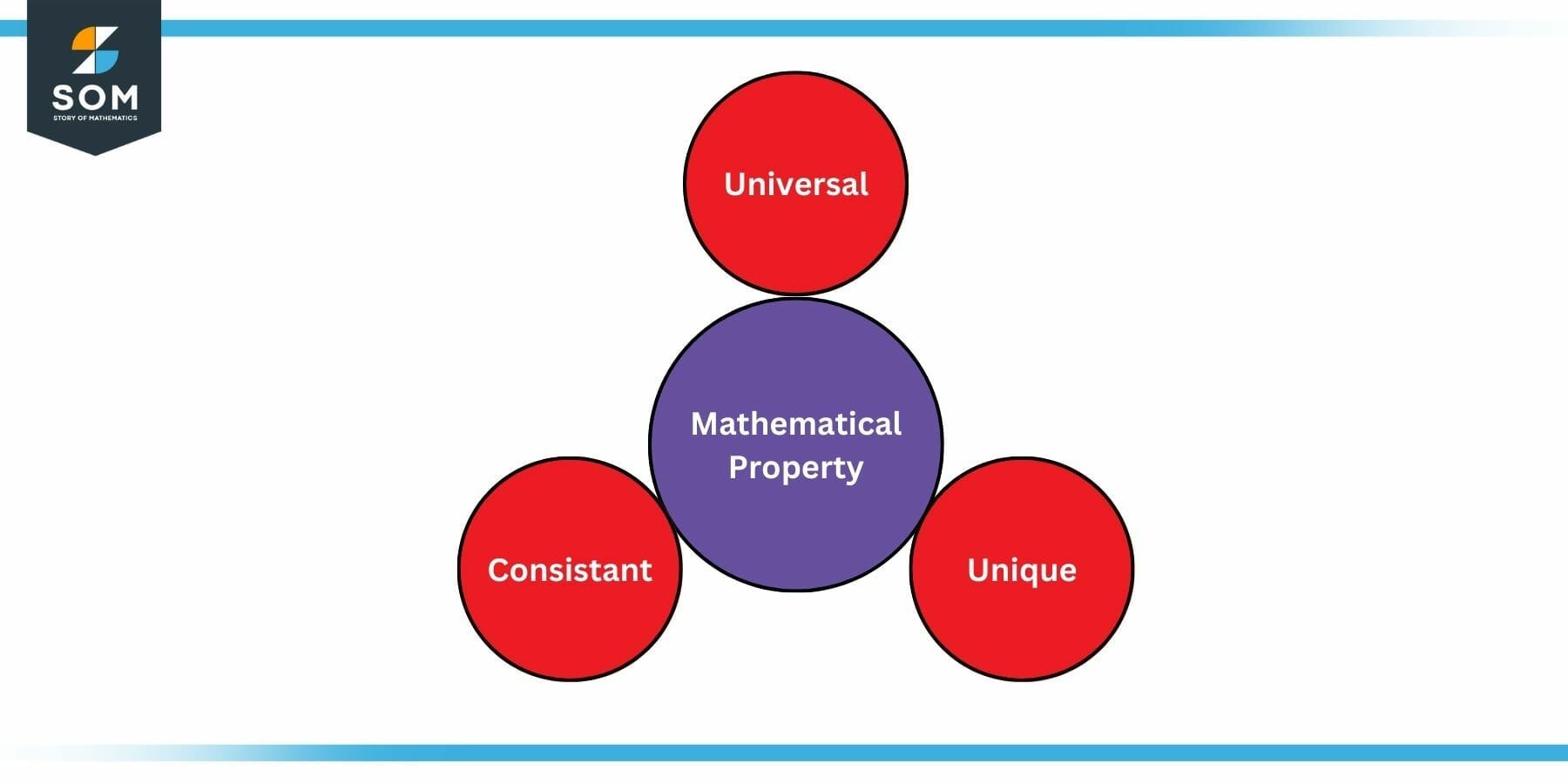
Figure 2: Qualities of Mathematical Property
A mathematical property is a characteristic of a mathematical object or concept that stays consistent and unchanged regardless of the context in which it is used. It is a fundamental aspect of mathematics that provides a basis for mathematical reasoning and problem-solving.
Significance of Mathematical Property
Properties play a critical role in many areas of science, technology, engineering, and mathematics. These properties define, identify, and describe mathematical objects and concepts and are used in many areas of mathematics, including arithmetic, algebra, calculus, geometry, and others.
Understanding these properties is essential for solving mathematical problems and for making mathematical arguments.
Examples of Mathematical Properties
Properties in Arithmetic
Equality Property
One of the most basic mathematical properties is the concept of equality. For example, the property of equality states that if two expressions are equal, then they can be used interchangeably in any mathematical calculation.
This property is often used in arithmetic and algebra, where it is critical to determine whether two expressions are equal in order to perform operations such as division, multiplication, subtraction, and addition.
Inverse Operations
Another important property in mathematics is the concept of inverse operations. Inverse operations are any two operations that undo each other, much like how subtraction undoes addition so they are inverse operations. This is true because subtracting a number from some other number is the same as adding the opposite of that number to it.
Similarly, multiplication and division are inverse operations, as dividing a number x by another number y is the same as multiplying x by the reciprocal of y.
Congruence Property
In geometry, the concept of congruence is an important property. Congruence refers to the similarity of two geometric figures in size and shape. Two figures are congruent if they have the same shape and size and can be superimposed on each other exactly.
This property is widely used in geometry to determine the properties of lines, angles, triangles, and other geometric figures.
Properties of a Geometric Shape
Let us consider the example of a unit sphere and a unit cube for the sake of this section.
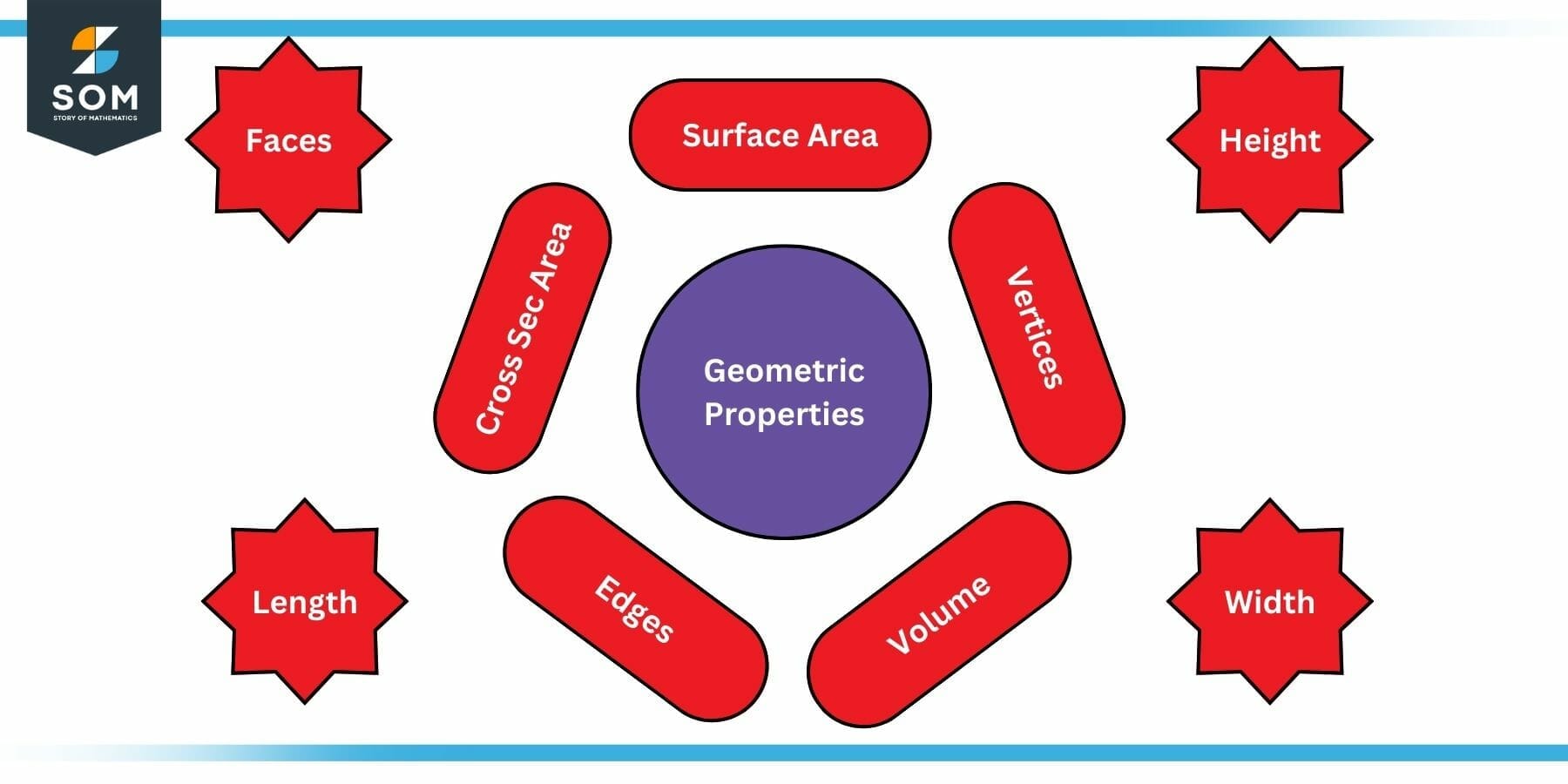
Figure 3: Geometric Properties
A geometric shape can be characterized and described with the help of its mathematical properties. Following are some of the chief properties among them:
- Perimeter: The sum of all edge lengths or side lengths of a geometric shape is called the perimeter. For example, the maximum perimeter of the unit sphere is 2$\pi$.
- Surface Area: The space occupied by a 2D shape in a 2D cartesian plane is called the area. For example, the maximum surface area of a unit sphere is 4$\pi$.
- Length: The measured distance between two extreme vertices of a geometric shape along the first dimension is called its length. Unit cube has a length of 1.
- Width: The measured distance between two extreme vertices of a geometric shape along the second dimension is called its width. Unit cube has a width of 1.
- Height: The measured distance between two extreme vertices of a geometric shape along the third dimension is called its height. Unit cube has a height of 1.
- Faces: The flat surfaces (all points have the same surface normal) of a geometric shape are called their faces. Unit cube has 6 faces. The unit sphere has no faces.
- Vertices: The points where edges meet are called vertices of a geometric shape. Unit cube has 8 vertices. Unit sphere has no vertices.
- Edges: The lines along which the faces of a geometric shape meet are called its edges. Unit cube has 12 edges. The unit sphere has no edges.
- Volume: The space occupied by a 3D shape in the 3D cartesian plane is called volume. For example, the maximum perimeter of the unit sphere is 4$\pi$/3.
Properties of Set Theory
Five properties are commonly used in set theory. These are:
- Commutative property: If the order of inputs does not change the result of a mathematical operator, then it’s called a commutative property.
- Associative property: If the grouping of inputs does not change the final results of a mathematical operator, then it’s called an associative property.
- Distributive property: If the result of an operator is invariant to the fact that this operator is applied to a group or an individual input, then it’s called distributive property.
- Identity property: The existence of a number that is unaffected by a mathematical operator is called identity property.
- Inverse property: The existence of a pair of numbers such that when a mathematical operator is applied to the pair, results in the identity is called inverse property.
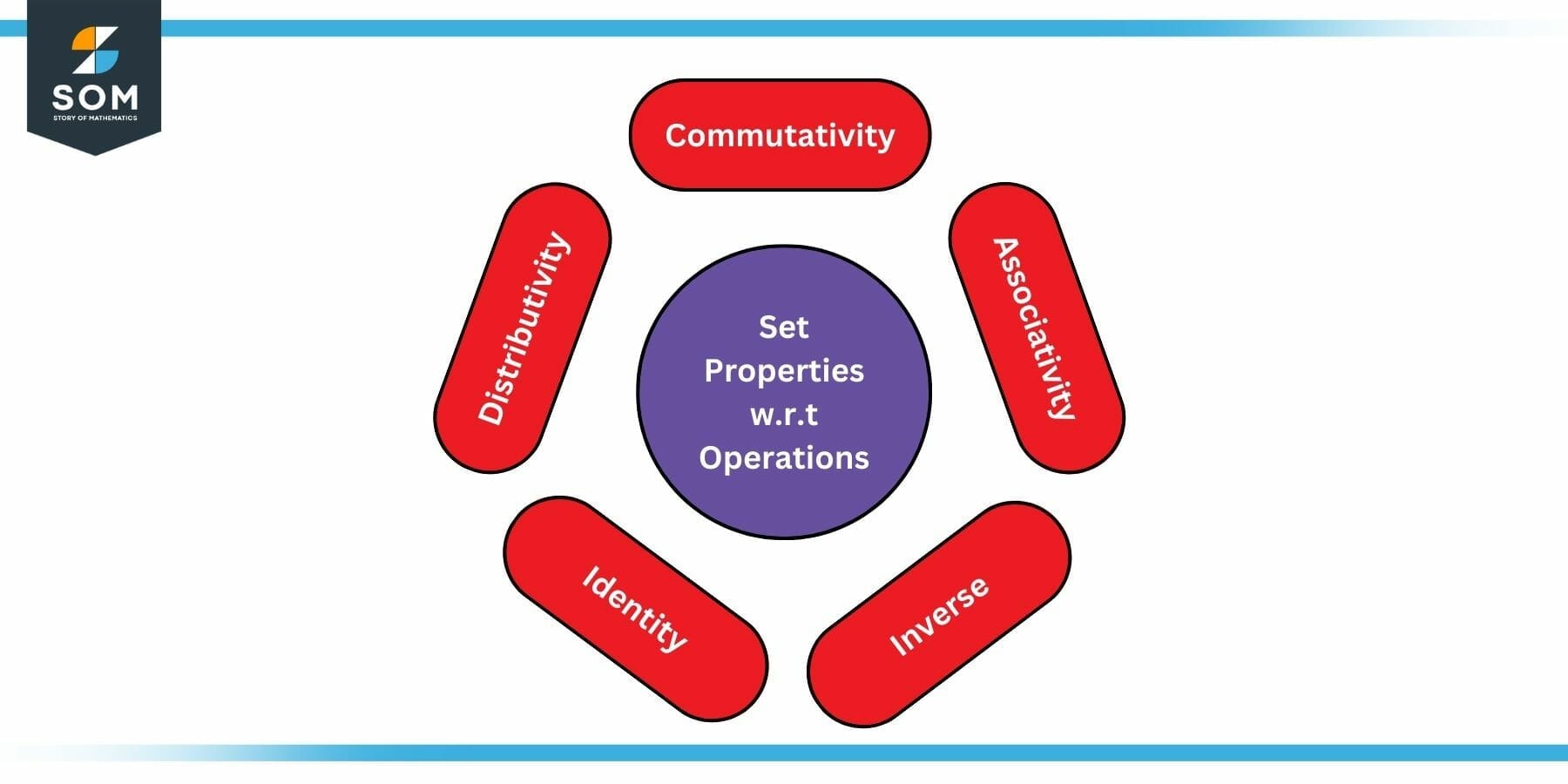
Figure 4: Set Properties
Properties in Trigonometry
There are three most fundamental trigonometric properties known to us, which are often called trigonometric identities. These include:
\[ \sin^2\theta + \cos^2\theta = 1 \]
\[ 1 + \tan^2\theta = \sec^2\theta \]
\[ 1 + \cot^2\theta = \csc^2\theta \]
Where sin, cos, tan, csc, sec, and cot are the sine, cosine, tangent, cosecant, secant, and cotangent functions, respectively.
Numerical Examples of Property
Now that we have good background knowledge of what the property is, we can solve some numerical problems.
Example 1
List some mathematical properties of a cube with a side length of 2 meters.
Solution
Using the geometrical properties discussed earlier, we can find that:
- Perimeter = 12 x 2 = 24 meters
- Surface Area = 6 x 2 x 2 = 24 square meters
- Length = 2 meters
- Width = 2 meters
- Height = 2 meters
- Faces = 6
- Vertices = 8
- Edges = 12
- Volume = 2 x 2 x 2 = 8 cubic meters
Example 2
Prove that $ \sec^2\theta + \csc^2\theta = \sec^2\theta \ \csc^2\theta $ using mathematical properties.
Solution
Consider the following trigonometric identity:
\[ \sin^2\theta + \cos^2\theta = 1 \]
Substituting $ \sin^2\theta = \dfrac{ 1 }{ \csc^2\theta } $ and $ \cos^2\theta = \dfrac{ 1 }{ \sec^2\theta } $ in above equation:
\[ \dfrac{ 1 }{ \csc^2\theta } + \dfrac{ 1 }{ \sec^2\theta } = 1 \]
\[ \dfrac{ \sec^2\theta + \csc^2\theta }{ \csc^2\theta \ \sec^2\theta} = 1 \]
\[ \sec^2\theta + \csc^2\theta = \csc^2\theta \ \sec^2\theta \]
Hence proved.
All images were created with GeoGebra.
