JUMP TO TOPIC
Protractror|Definition & Meaning
Definition
The protractor is a geometrical instrument used to measure and draw angles. It is shaped like a semicircle, with markings and lines indicating various angles (degrees) in both the clockwise and anti-clockwise directions. Some people call it a “D” since it looks much like the letter “D.”
The shape of the protractor is shown in Figure 1 below.
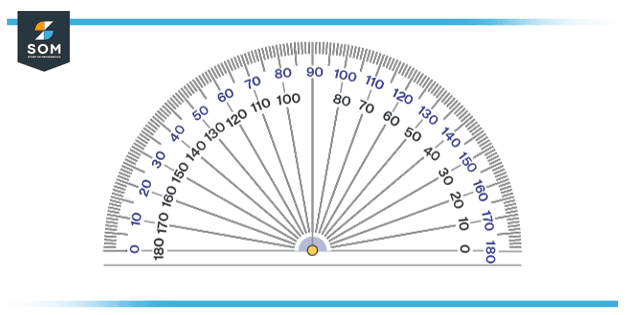
Figure 1: Shape of the protractor
As shown in Figure 1, a protractor is a semicircular geometry instrument that is divided into 180 identical cuts, apiece counting 1°. It is utilized for marking and sketching inclinations of known dimensions and finding inclinations of unknown dimensions and is usually constructed of transparent plastic, glass, steel, or wood.
The geometry protractor has 2 graduated scales sketched on it i.e., outer and inner. The outer scale begins from 0° and ranges up to 180° in clockwise order, and the inner scale has an identical range in counterclockwise order.
A protractor is an easy measuring tool that is utilized to gauge angles. A typical protractor is in the form of a semicircle with an internal scale and an external scale and with graduations marked from 0° to 180° on it. Designers utilize a more accurate protractor called an arc protractor instrument which gives more accurate readings.
Protractors have been in service since the 17th century. By the 18th century, protractors were widely utilized in geometry and mathematics. Some protractors are straightforward half-discs or full circles. More refined protractors (e.g., bevel protractors) have one or two swinging arms to help gauge the inclination.
A protractor, in mathematics, is supposed to be a critical measuring tool that is in the form of a semi-circle. A common protractor is a translucent tool that permits one to gauge angles in degrees.
A radian scale protractor gauges an angle in radians. If one observes carefully, one may see that a typical protractor has degrees labeled clockwise from 0° to 180° on the outer scale and counter-clockwise from 0° to 180° on the inner scale.
What Is a Protractor Used For?
Youths understand how to utilize these instruments in mathematics tasks and, in particular, when understanding the properties of shapes. The rationale behind why protractors are utilized in mathematical schooling is that they equip juniors with the prospect of setting their learning into practice.
For example, students not only understand the concepts of various inclinations in theory, but they will also learn how to measure and draw angles. Major types of angle classes students learn include the following:
- Right angles
- Acute angles
- Obtuse angles
- Straight angles
- Reflex angles
By getting some hands-on experience, youth are more likely to attain information for longer.
Measuring Angles With a Protractor
Generically, to gauge an angle by utilizing a protractor, one needs to follow the steps given below.
- Align the vertex of the inclination with the dot at the middle of the protractor.
- Align one side of the inclination with 0 degrees on the protractor.
- Read the protractor to note where the other side of the angle intersects the number scale. Most protractors have two number scales. It’s important to use the same number scale for both sides of the angle.
A protractor is an instrument that is very uncomplicated to use. It has 2 readings – the outer reading and the inner reading that help to reckon an inclination. A protractor may be read utilizing its interior readings or its exterior readings depending on the inclination that is created.
Each interior and exterior measurement complements each other, i.e., these readings add up to 180°. e.g., 10° + 170° = 180°, 20° + 160° = 180° etc. The steps involved in measuring the angle are summarized below and are depicted in Figure 2.
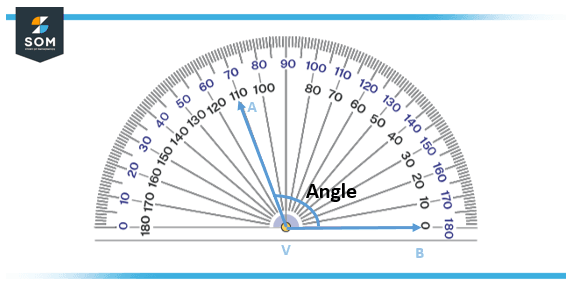
Figure 2: How to measure the angle
- Step 1: Place the center (dot) of the protractor on the vertex V.
- Step 2: Place the base of the protractor on the beam, which is the base of the inclination labeled as B.
- Step 3: Now choose which measurements are to be observed. If the inclination to be gauged is on the left-hand side from the middle of the protractor, one has to utilize the external graduation of the protractor.
- Step 4: If the inclination to be gauged is at the right-hand side from the middle of the protractor, one has to utilize the internal graduation of the protractor.
Sketching Angles With a Protractor
To sketch angles by utilizing a protractor, one needs to go through the subsequent steps. For demonstration, Allow us to see how to sketch an inclination of 60º utilizing a protractor. The summary of the same process is depicted in Figure 3 below.
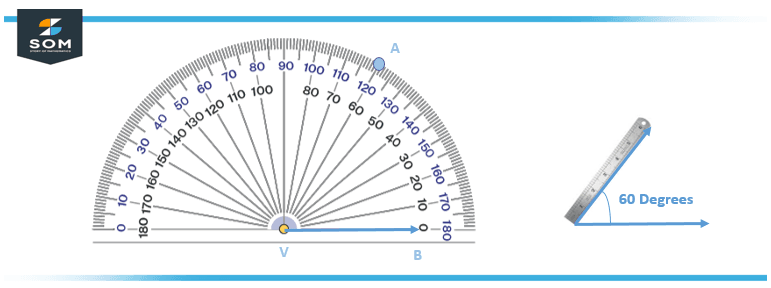
Figure 3: Drawing an angle using a protractor
- Step 1: Draw a baseline VB.
- Step 2: Align the base of the protractor on VB so that the middle of the protractor is positioned on point V.
- Step 3: As the inclination is sketched on the right-hand side of the vertex ‘V,’ the inner scale for readings needs to be used.
- Step 4: In the inner scale, look for 60º and mark it as a point A.
- Step 5: Now, using a scale, join V and A. Therefore, ∠AVB = 60°.
360° Protractor
A 360° protractor is circular in formation and carries gradings up to 360° in clockwise order. It is typically utilized in the area of architecture, mechanical drawings, meteorology, etc. One may also use a 360° protractor to sketch a reflex angle. The inclination protractor tool and 360° protractor give more accurate measurements.
If the inclination to be measured is on the left-hand side from the middle of the protractor, one needs to use the outer readings of the protractor and if the angle to be measured is on the right-hand side of the middle, one needs to use the inner readings. As a precaution, one needs to align the baseline and vertex properly in order to reduce errors.
Solved Examples for Specific Cases
Example 1
Find the measurement of each inclination of an equilateral triangle having vertices ABC with the use of a protractor.
Solution
Align the protractor with the vertices of △ABC. Record the angle acquired in each case. One will see that all the inclinations of the equilateral triangle measure 60°.
Example 2
What will be the inclination created at vertex B of the square that has vertices ABCD?
Solution
In order to find inclination at vertex B, place the middle of the protractor at vertex B with either AB or BC overlapping with the baseline and note the measurement. One will get a 90° angle.
All images/mathematical drawings were created with GeoGebra.
