Quadrangle|Definition & Meaning

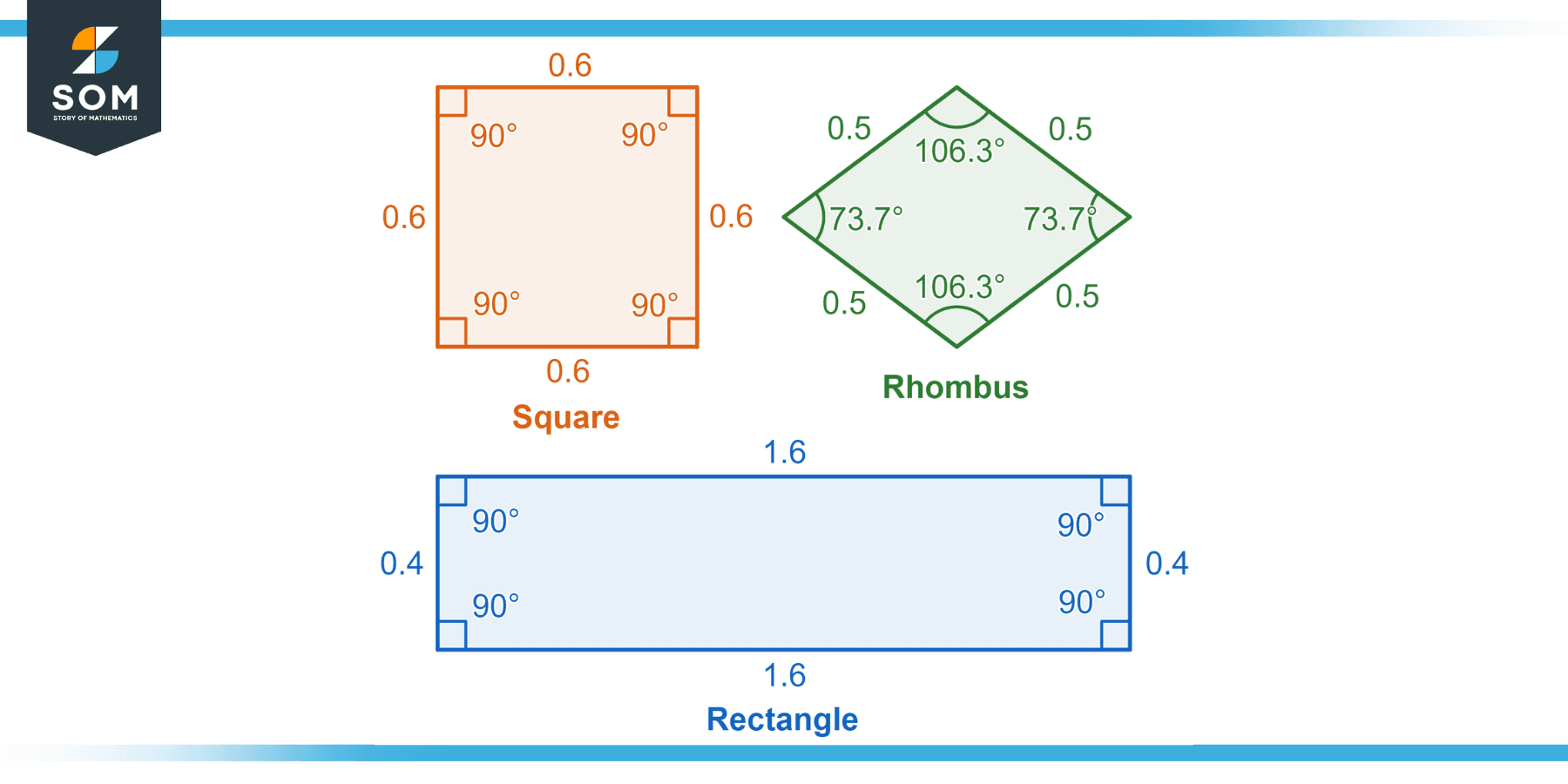
Figure 1 – Various different quadrangles and their measurements

Types of Quadrangle 

Quadrangles are divided into different types depending on the properties of the sides and angles. The different types of quadrangles are square, rectangle, parallelogram, rhombus, trapezoid, and kite. Each of these is explained below.

Square

A square is a type of quadrangle in which all four sides’ lengths are equal. The angles in a square are all right angles (measuring 90 degrees). This means that the adjacent sides in a square are all perpendicular. Consequently, the opposite sides are parallel. The area of a square where every side’s length equals a is given by a². 

Rectangle

Rectangle is another common quadrangle in which the opposite sides are equal and parallel. Similar to a square, the interior angles are all right angles in a rectangle and the adjacent sides are perpendicular to each other. The sides of a rectangle are commonly referred to as length and width. The area of a rectangle having length a and width b is given by a $\times$ b. 

Rhombus

A quadrangle in which all four sides are equal in length (same as a square) but the interior angles are not all equal is called a rhombus. In a rhombus, the opposite angles are equal. A square is a special type of rhombus in which all the interior angles are right angles. 

For a rhombus with each side equal to a, and diagonals given by d1 and d2 the area is given by:

Area = (d1 x d2) / 2

Another representation for the area involves the interior angle and the length of the side of the rhombus. Let the side of the rhombus be given by a with one of the interior angles given by $\theta$. The area is given by:

Area = a² $\times \sin{\theta}$

Parallelogram

A parallelogram is a type of quadrangle in which the opposite sides are both parallel and equal in length. Since the opposite sides are equal in length and parallel to each other, this results in the opposite angles being equal as well. A parallelogram having sides length of a and b with height h – which is the perpendicular distance between opposite sides – has an area of b x h. 

A parallelogram’s area can also be completely defined by the lengths of the sides, but it also requires knowledge about the angle between the two sides. If the angle between the sides a and b is $\theta$, then the area is given by:

Area = ab $\sin({\theta})$

Note from the definition of a parallelogram that square, rectangle, and rhombus are all special cases for the parallelogram and are all parallelograms in themselves since all of them have their opposite sides and angles as equal and parallel as well.

Trapezoid

A trapezoid is a quadrangle in which one pair of opposite sides are parallel to each other. The two parallel sides are referred to as the bases of the trapezoid. The shortest distance between the two bases is called the height of the trapezoid. 

The area of a trapezoid is calculated based on the lengths of the parallel sides and the distance between them – the height of the trapezoid. The area with bases a and b with height h is given by:

Area = (a + b) x (h / 2)

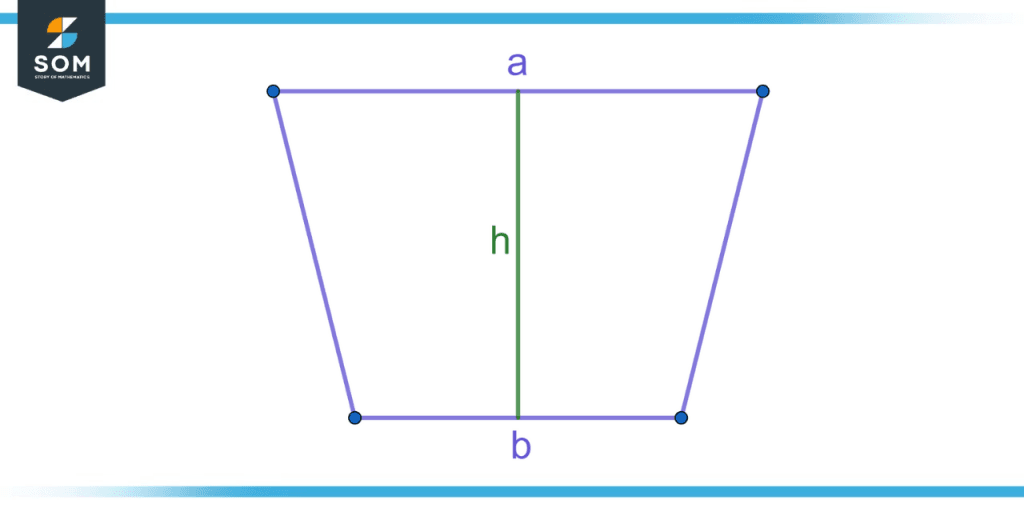
Figure 2 – A trapezoid with bases a and b and height h.

A special type of trapezoid in which the lengths of the two parallel bases are equal is called an isosceles trapezoid. 

Note that the shape of trapezoid is referred to as a trapezium in the UK. 

Kite

Kite is a quadrangle in which the adjacent sides are equal in length. Since there are a total of four sides in a kite – it being a quadrangle – there are two pairs of equal sides in a kite. The two points where the unequal sides meet have equal angles. 

The diagonals of a kite show some interesting properties. The diagonals meet at right angle. Also, the longer of the two diagonals – also called as main diagonal – bisects the other diagonal i.e., cuts the smaller diagonal into half at the intersection point. 

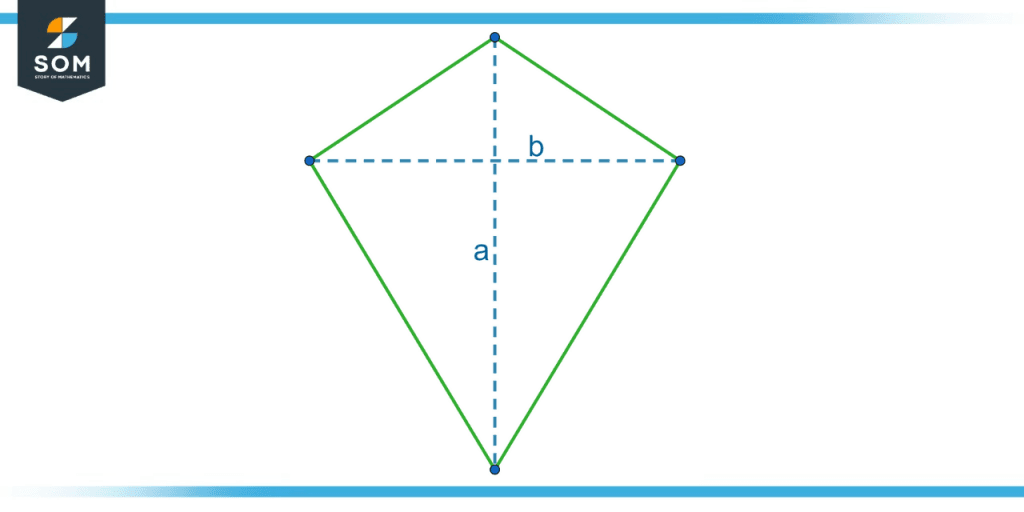
Figure 3 – A kite with its diagonals a and b.

The area of a kite can be computed directly from the diagonals as well. Let the bigger diagonal be a, and the smaller diagonal be b. Then the area of the kite is given by:

Area = (ab) / 2

Thus, it is half of the product of the two diagonals.

Regular and Irregular Quadrangles

Quadrangles are also classified as regular and irregular quadrangles. A quadrangle in which all the sides and angles have equal measure is called a regular quadrangle. The quadrangles that do not have all the sides and angles of equal measure are called irregular quadrangles. 

From the definitions of the different types of quadrangles above, it can be noted that only a square is a quadrangle in which all the angles and sides have equal lengths. Thus, a square is the only regular quadrangle. All the other types of quadrangles are irregular. 

An Example of a Quadrangle

John wants to hire a cleaning for his newly acquired farm, which roughly resembles a parallelogram. He knows that the measures of the two adjacent sides of the farm are 23 and 18 meters, respectively. He also measures the shortest distance between the two opposite sides of 23 meters each is 20 meters. The cleaning company bills at the rate of 1.3 dollars per square meter. Compute the cost for John.

Solution

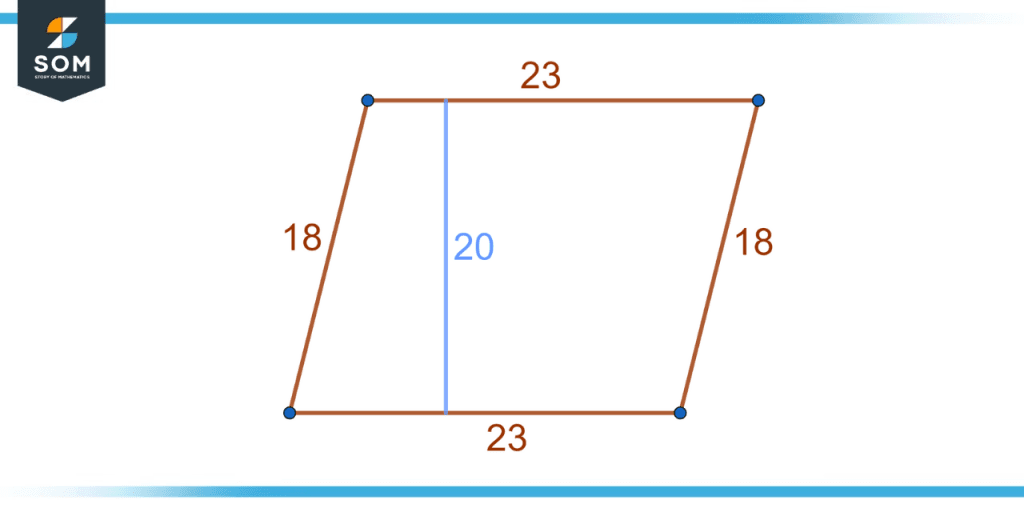
Figure 4 – Parallelogram representing the measures of John’s farm.

Note that the cost is proportional to the square meters, which is a unit of the area. This means that the area of the farm is required for the calculation of the total cost.

It is given that the farm resembles a parallelogram. Recall that the area of a parallelogram can be computed from the length of its base and height. The height of the parallelogram is the shortest distance between the bases. The height is given as 20 meters and the base is 23 meters. The area is thus:

Area = 20 x 23

Area = 460 square meters

The cost will be the product of the total square meters and the per square meter cost. The per unit area cost is given as 1.3 dollars, and the computed area is 460 units. Thus, the total cost will be:

Cost = 460 x 1.2

Cost = 552 dollars

Thus, the total cost for John will be 552 dollars.