Quadrant (Circle)|Definition & Meaning

Consider a circle having two radii r1 and r2 that are at right angles to each other (90 degrees). The arc connecting the two radii will be taken as a quadrant of a circle. 

Representation

Here is the representation of the quadrant of a circle, the red portion constitutes the quadrant which is typically a one-fourth portion of a whole circle.

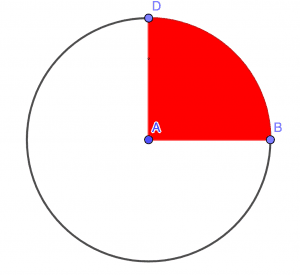
Figure – 1 Quadrant of Circle Representation

If we bisect the circle into four equal parts, then we get the following quadrants.

Quadrant 1

ABC is the first quadrant of the circle as shown in the figure below.

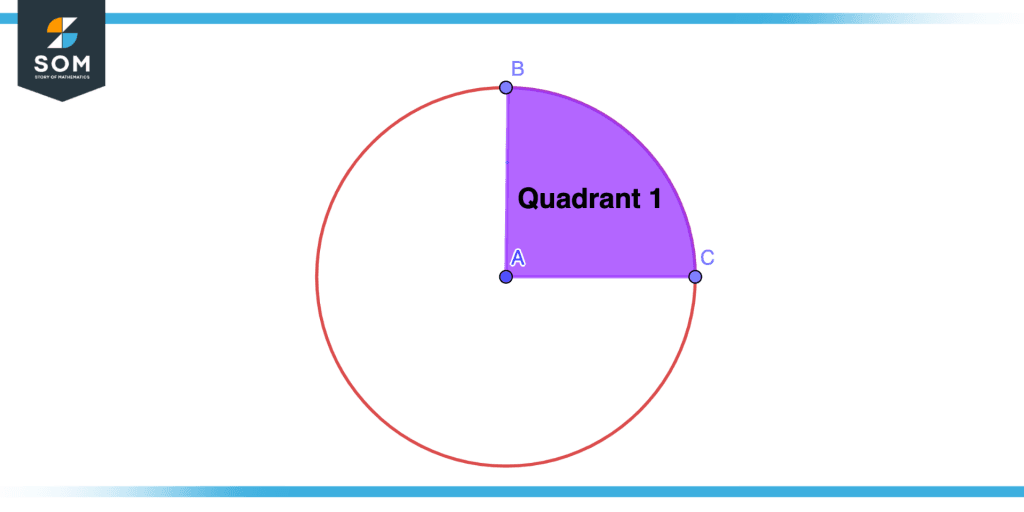
Figure – 2 First Quadrant of Circle

Quadrant 2

AED is the second quadrant of the circle as shown in the figure below.

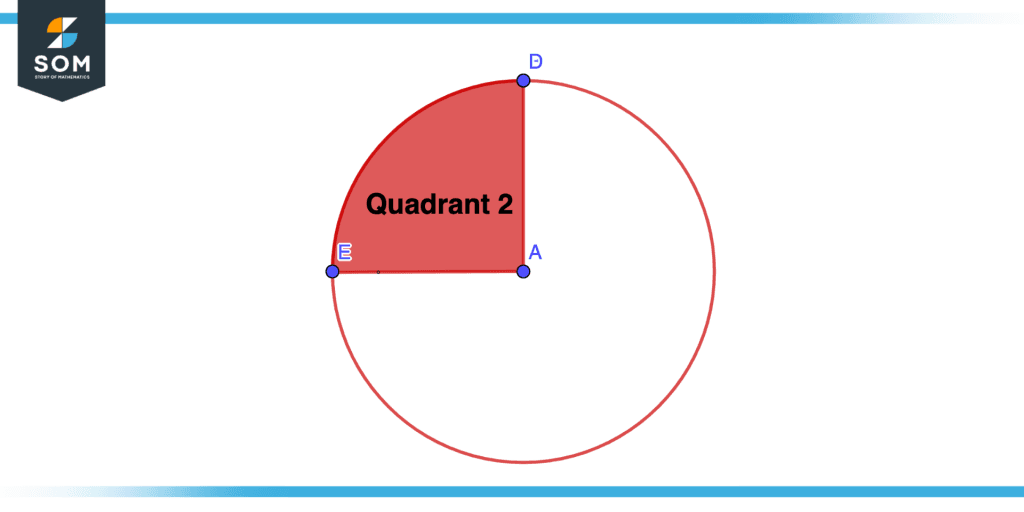
Figure – 3 Second Quadrant of Circle

Quadrant 3

AFG is the third quadrant of the circle as shown in the figure below.

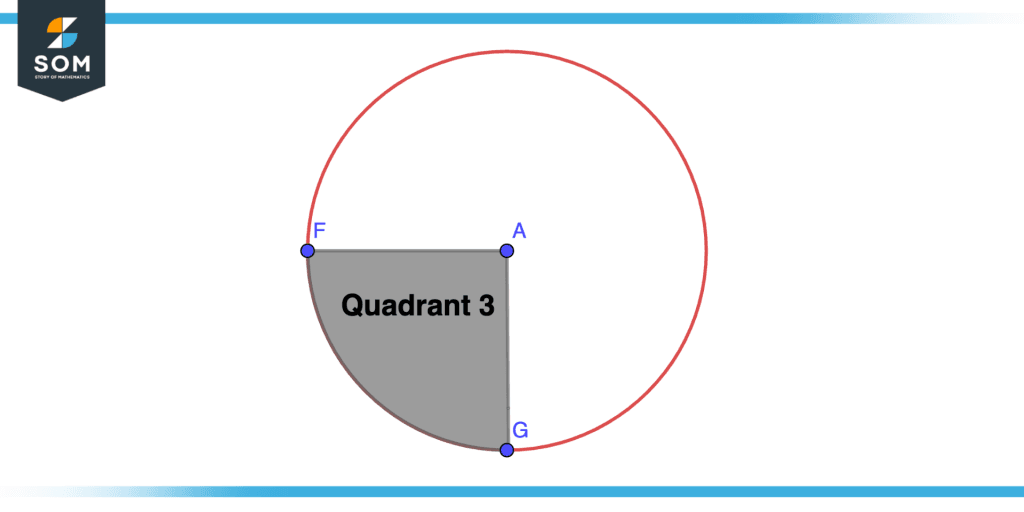
Figure 4 – Third Quadrant of Circle

Quadrant 4

AKL is the fourth quadrant of the circle as shown in the figure below.

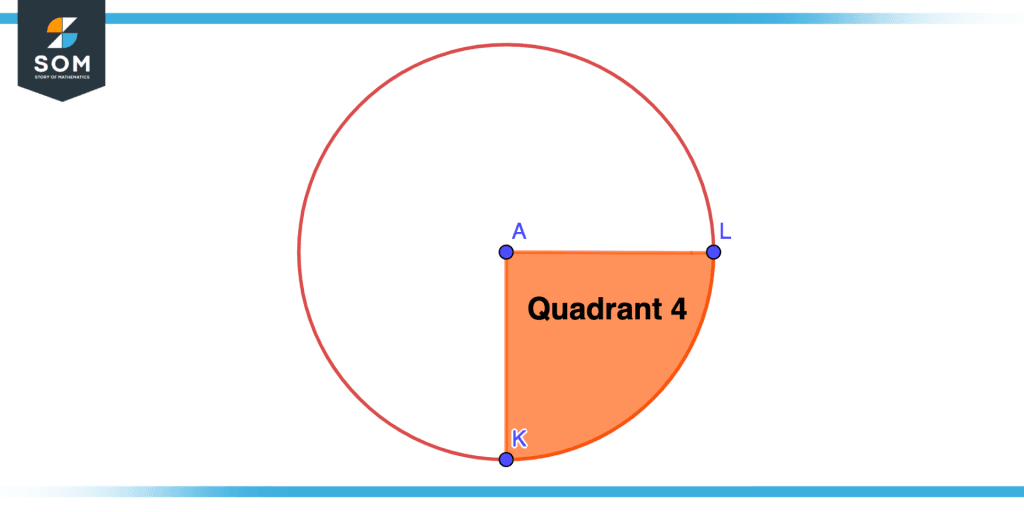
Figure 5 – Fourth Quadrant of Circle

Properties of Quadrant of Circle

1. The quadrant must be a sector of 90 degrees.
2. The radii that form the quadrant must be at the right angle to each other.
3. The area of one quadrant must not overlap with any of the other three quadrants to maintain the 4 equal quadrants (the circle has four quadrants).

Steps to Make a Quadrant of a Circle

Step 1

From the center of the circle sketch a line to any point on the circle.

Step 2

Sketch another line that must be at a right angle to the above like drawn (90-degree).

Step 3

The arc joining the above two lines including the center and radii will be referred to as a quadrant of the circle.

Constructing a Quadrant of a Circle Practically

Step 1

Consider below the circle having a center A. We will take a point in a circle to let us suppose B now we will join the points A and B as shown. We can call the line segment AB as radius or radii 1 of the circle.

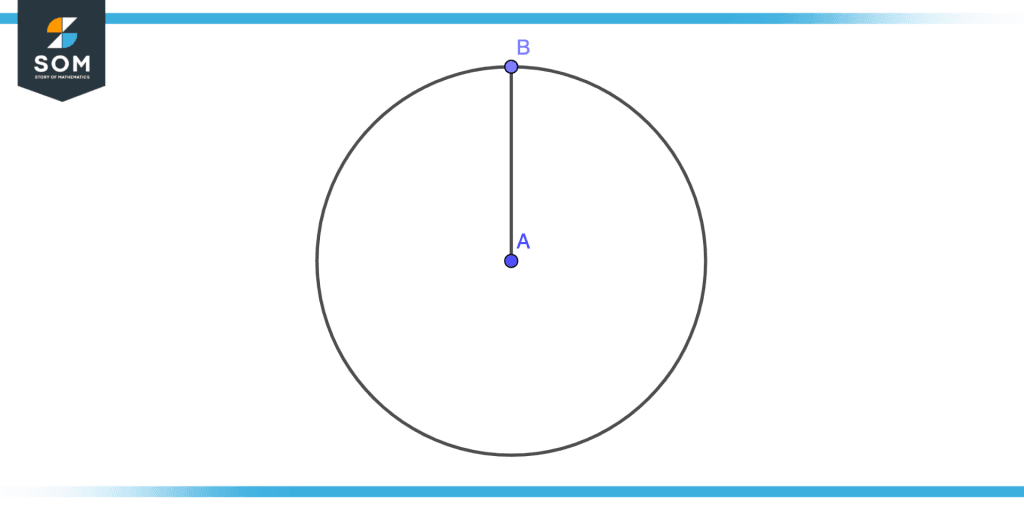
Figure 6 – Constructing Quadrant Step One

Step 2

Consider another point suppose C on the circle but here we will apply the property of the quadrant, the supposed point must be in such a manner that it is at the right angle to the previous point A. Join given point C with the center of circle A, we get a line segment AC, take AC as the second radii of the circle that is the right angle to the line segment AB.

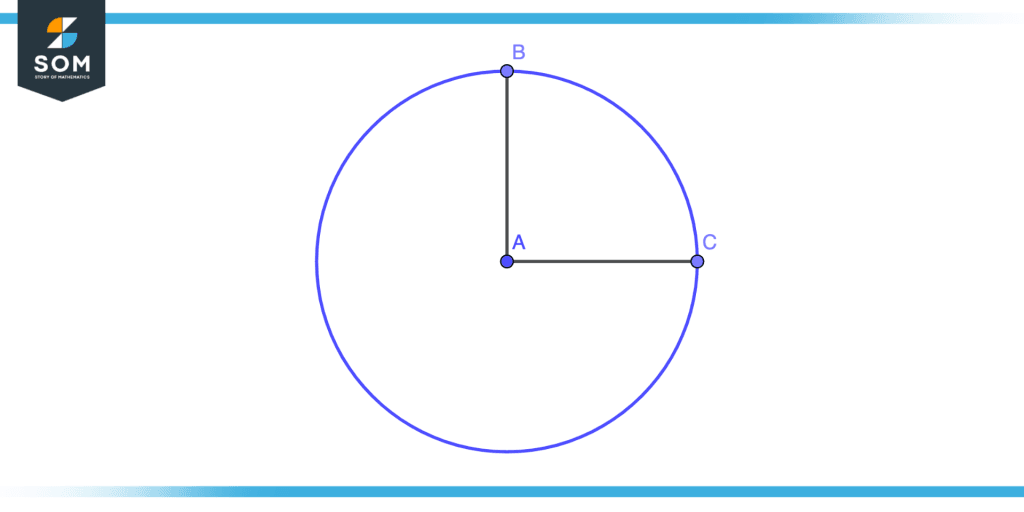
Figure 7 – Constructing Quadrant Step Two

Step 3

The arc joining the radii AB and AC along with the two radii constitute a quadrant of the circle as shown in the figure.

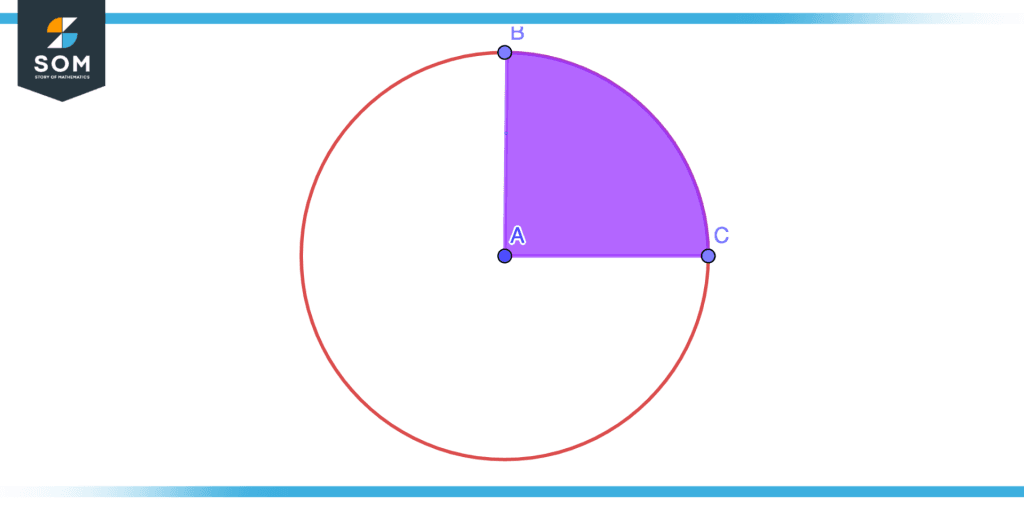
Figure 8 – Constructing Quadrant Step Three

Steps to Make a Circle From Its Quadrant

Step 1

Sketch two line segments of equal length.

Step 2

Join the above two lines together in such a way that they are at a right angle to each other and share a single common point.

Step 3

Connect the two uncommon points of the line segment with an arc .

Step 4

Repeat the above step three more times we have now four quadrants we join these four quadrants to a single common point that will eventually make the circle.

Constructing a Circle From Its Quadrant Practically

Step 1

Draw two line segments AD and EF of equal length as shown in the figure.

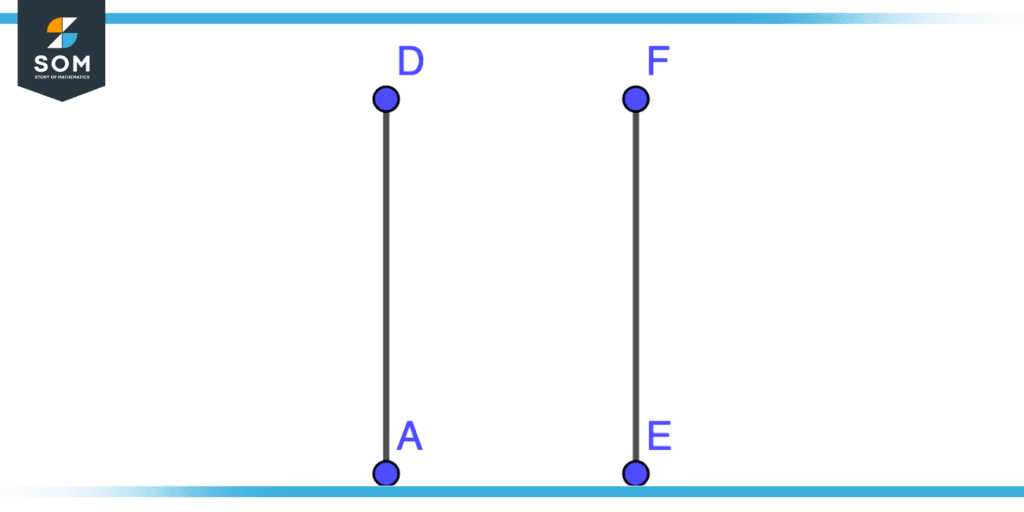
Figure 9 – Constructing Circle From Quadrant Step One

Step 2

Join AD and EF together in such a way they meet at single point A as shown in the figure we have now segments AD and AE and the angle between them is 90 degrees.

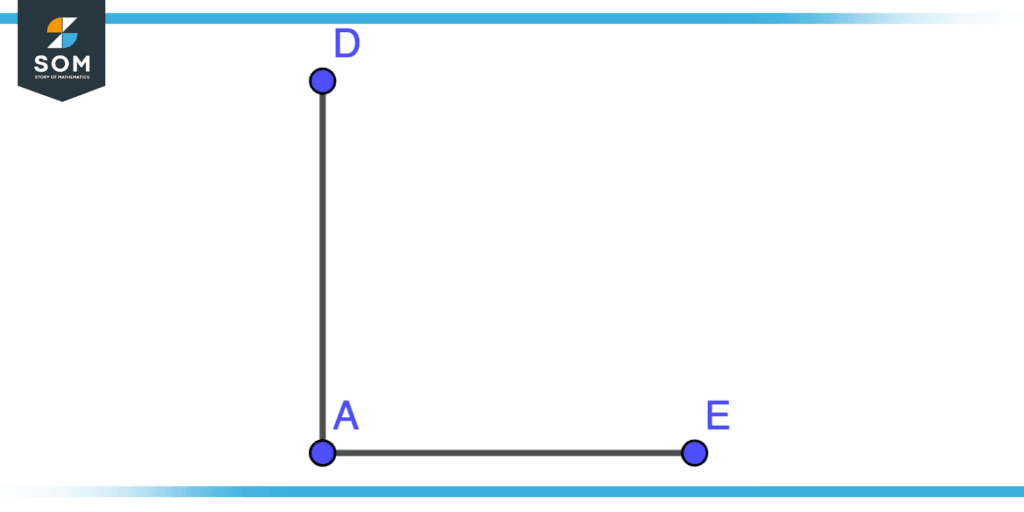
Figure 10 – Constructing Circle From Quadrant Step Two

Step 3

Connect the points D and E of segments AD and AE with an arc saying “C” as shown in the figure.

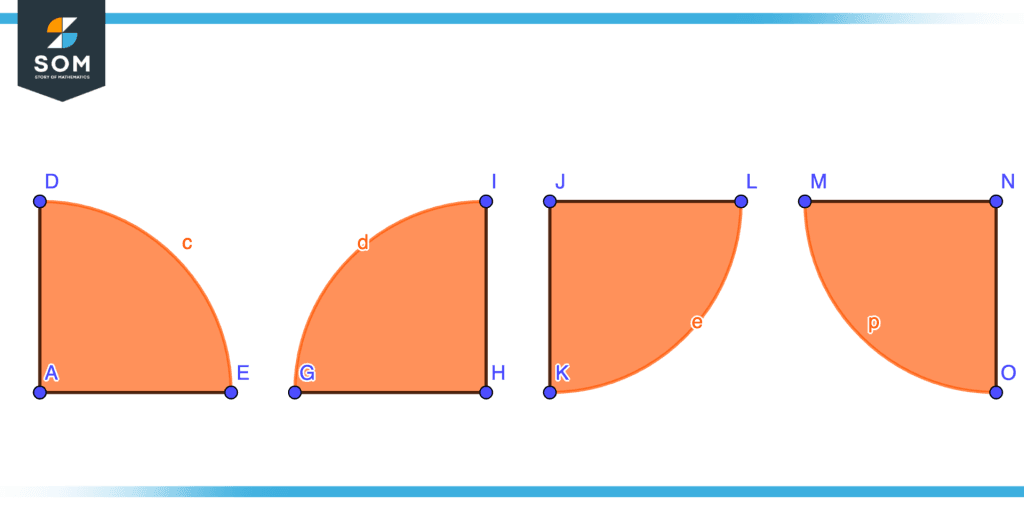
Figure 11 – Constructing Circle From Quadrant Step Three

Step 4

On repeating the above steps three more times we got four quadrants AED, HIG, JKL, and NMO we will now join these quadrants together in such a way that they share a single common point A. Finally, a circle is constructed and each quadrant is one-fourth portion of the whole circle.

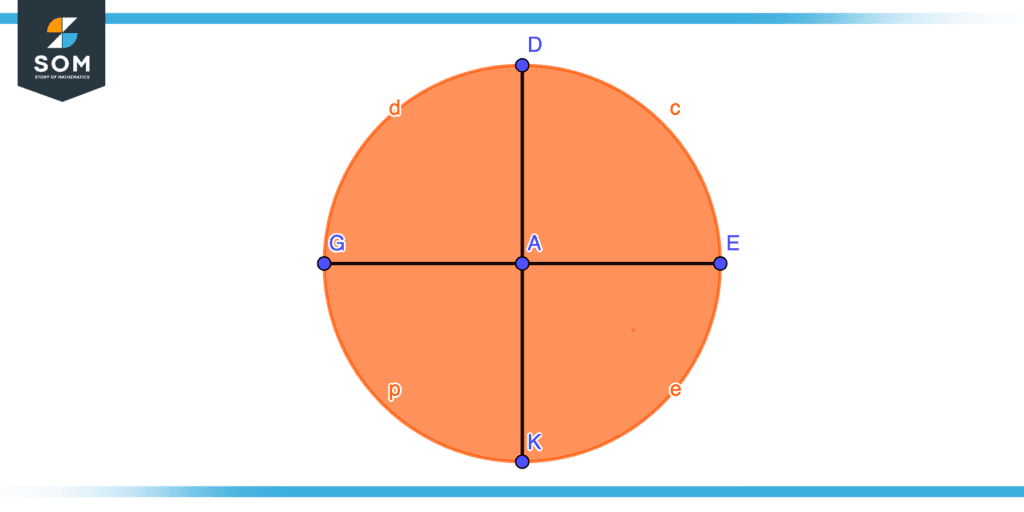
Figure 12 – Constructing Circle From Quadrant Step Four

Area of Quadrant

The area of the quadrant of a circle is generally equal to one-fourth times the area of the circle. Calculating a quadrant’s area requires knowing a circle’s area. We can calculate a circle’s area of quadrant by using the formula given below since a quadrant’s area is one-fourth of its total area.

Area of circle =$\pi r^{2}$

Area of Quadrant of circle =$\frac{1}{4} \times \pi r^{2} $

The Perimeter of the Quadrant

Quadrants of a circle have a perimeter that is one by four times the circumference and two times the radius. An angle between two points on a circle is also referred to as a quadrant’s circumference. The perimeter of a quadrant of a circle can be calculated by using the given formula.

Perimeter =$r(\frac{\pi}{2} +2)$

An Example of Identifying Quadrants of Circles

Consider the following figure to demonstrate which is the quadrant of a circle and which is not, and explain with reasons.

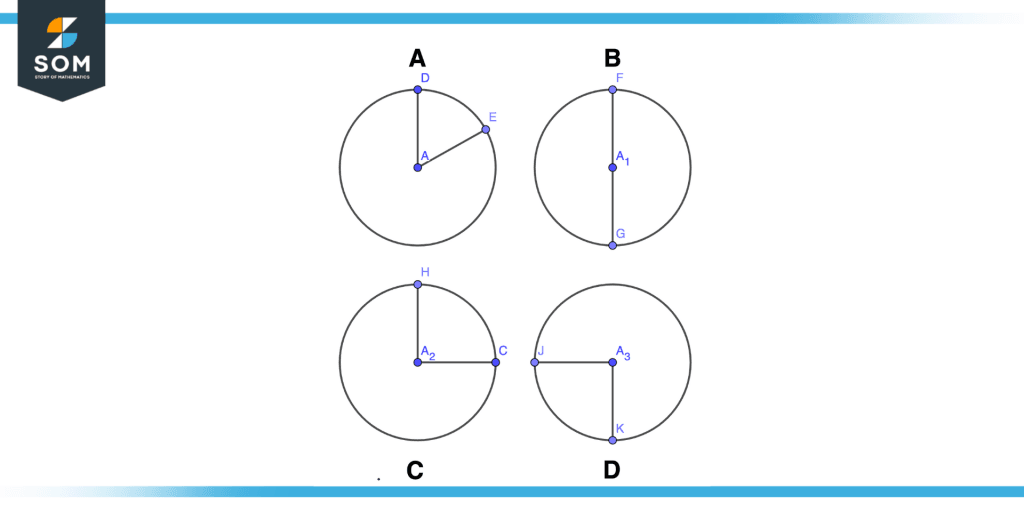
Figure 13 – Quadrant of Circle Example

Solution

In Figure A, there are two radii AD and AE. We can see that they are not right angles to each other rather they are at somewhat 60 degrees to each other, moreover AED is not one-fourth portion of the whole circle so we will conclude that AED is not a quadrant of the circle.

In Figure B, there are two radii AF and AG, we can visualize that these two radii are bisecting the circle into two parts moreover they are 180 degrees so AFG is not a quadrant of the circle.

In Figure C, there are two radii AC and AH. Both of the radii are right angle or 90 degrees to each other moreover it is constituting exactly one-fourth of the whole circle so ACH is referred to as the quadrant of the circle. Generally, the figure is representing the first quadrant of a circle

In Figure D, there are two radii AK and AJ both are perpendicular to each other i.e. 90 degrees moreover they are making one-fourth portion of the given circle also this is generally the third quadrant of a circle so  AKJ is the quadrant.

All mathematical drawings and images were created with GeoGebra.

Quadrangle Definition < Glossary Index > Quadratic Definition