JUMP TO TOPIC
Quadratic|Definition & Meaning
Definition
A quadratic is any term, expression, or equation where the variable’s highest power (or exponent) equals a square (power of 2 or $^2$). For example, x$^2$ is a quadratic term, and 3x$^2$ + 2x + 1 is a quadratic expression because of the quadratic term 3x$^2$.
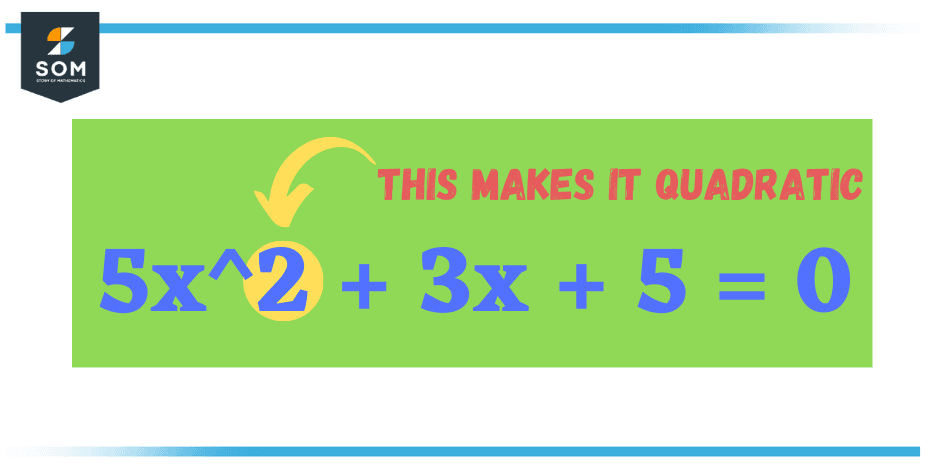
Figure 1 – General form of a quadratic
The definition of a quadratic as a squared linear equation demands that at least a single square component must be included. It even goes by the name of quadratic equations in general mathematics books. The known form of a quadratic is ax2 + bx + c. This polynomial equation contains two terms, a constant and a variable.
Here, a,b and c are the constants, also known as coefficients of variables, whereas x is known as the independent variable. The quadratic polynomial only stays quadratic when its 2nd-degree variable is not equal to zero. If it becomes equal to zero, the quadratic term roots out to be a linear equation like:
bx + c = 0
These contents are also known as quadratic coefficients.
What Is a Polynomial?
A mathematical expression containing various variables and constants is known as a polynomial. These expressions are known as algebraic expressions, and the variables are occasionally known as indeterminate.
Every arithmetic operation, such as multiplication, addition, and subtraction taught in junior years, can be performed on a polynomial.
A polynomial can have numerous variables as well as higher exponents depending upon the situation. A simple polynomial can be written as x + 1, which is a first-degree polynomial. Similarly, a quadratic equation is a 2nd-degree polynomial which we will be discussing in this article.
The definitive form of a polynomial is:
\[P(x) = a_nx^n +a_{n-1}x^{n-1} +a_{n-2}x^{n-2} + \ldots + a_1x + a_0 \]
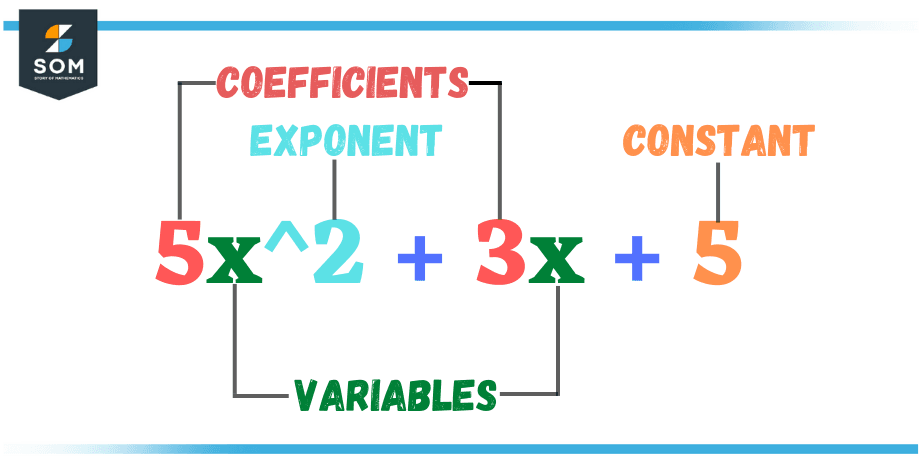
Figure 2 – Elements of a Quadratic equation
Degree of a Polynomial
Polynomials have exponential powers existing on indeterminate, and the highest exponent is regarded as the degree of the polynomial. A zero polynomial has an undefined degree, such as 6. Whereas a polynomial with a zero degree is a constant such as P(x) = 6. Some higher-order polynomials are given below
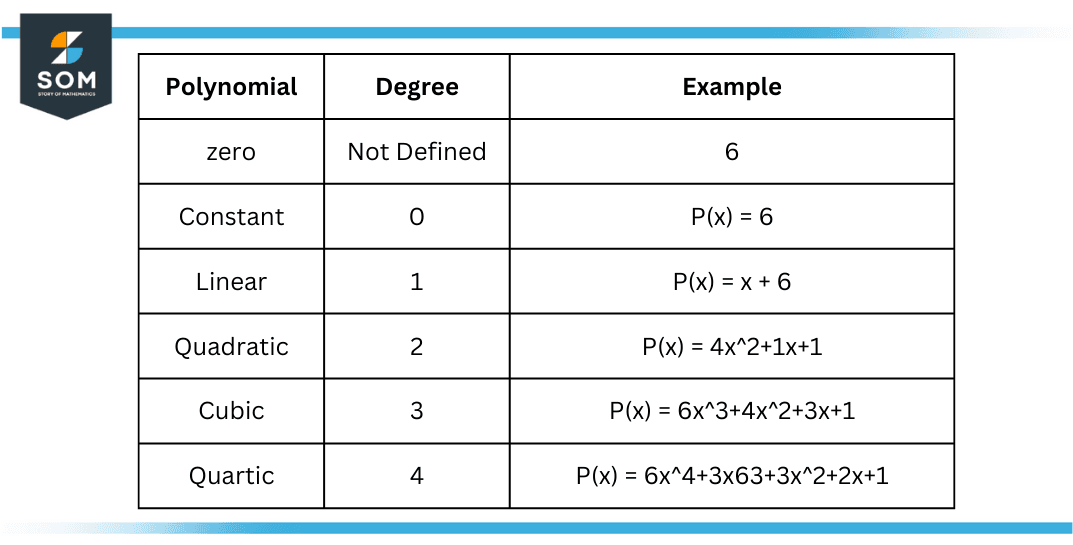
Figure 3 – Degree of Polynomials
Quadratics Function
A quadratic polynomial is such a polynomial that will have at least one variable of 2nd-degree, or it may have more than one 2nd-degree variable. A function that is represented by such a polynomial is known as a quadratic function. A quadratic equation can be constructed if a quadratic function is made equal to zero. The zeros of the associated quadratic function serve as the solutions to quadratic equations.
A quadratic function is written in the form of:
f(x) = ax2 + bx + c
A curve known as a parabola forms the graph of a quadratic function.
Although the “breadth” or “angle of inclination” of a parabola can vary as well as its direction of opening, they always possess the same fundamental “U” form. If the coefficient “a” is positive, the graph will be an upwards facing “U,” whereas it will be facing downwards if “a” is negative.
Quadratics Formula
The quadratics formula is used to solve the quadratic equation for the value of its indeterminate. In other words, we use the quadratics formula to uncover the roots of a quadratic equation. A quadratic equation of the form ax2 + bx + c can be solved using the following quadratic formula:
\[ x = \dfrac{-b \pm \sqrt{b^2 – 4ac}}{2a} \]
How To Solve Quadratics?
The quadratics equation can be solved in numerous ways, but in everyday practice, the following methods are the most common ones,
Factoring the Quadratics
The following pointers must be fulfilled to factorize a quadratic:
- Start by solving the equation ax2 + bx + c.
- Make sure the zero setting is appropriate.
- Assume the right part of the quadratic has a value equal to zero and factorize the left-hand side of the equation.
- Give each component a value of nonentity. The x values can now be found by solving the quadratic.
If you encounter a case where the coefficient of the highest degree monomial is not equal to 1, then purposefully, you have to come up with a strategy to find the appropriate arrangement of the factors.
Completing Square
One approach to locating the roots of a quadratic is by using the completing square method. With this approach, the given quadratic must be first transformed into an ideal square.
The following steps must be fulfilled to complete the square of a quadratic:
- Construct the equation in the format so that “c” appears on the right-hand side.
- Reduce “a” from the whole equation to ensure that the coefficient of x2 is equivalent to 1. This action is only necessary if “a” is not 1.
- Now add $\left(\frac{b}{2a}\right)^2$ across halves, which is half of the coefficient of x-term under a square.
- The left-hand part of the quadratic should be factored as a complete square.
- Calculate the square roots of each side.
- Calculate the roots of the x indeterminate.
Quadratics Formula
We have already discussed the quadratics formula in detail to find the roots of any quadratic equation. Upon solving the equation using this formula, the final solution must have two answers, as the highest degree of this polynomial is equal to two. The formula is
\[ x = \dfrac{-b \pm \sqrt{b^2 – 4ac}}{2a} \]
Here, the plus-minus signs show us that the solution will contain two distinguishable roots of x.
Square Root of Special Quadratics
This method can only be applied if there is a possible equation that will have a square on both sides, such that their square root is feasible. Such as x2 + b2 = 0. This type of equation can be easily solved using the square root method, and it will result in two identical roots but with different signs.
Quadratic Irrationals
In mathematics, irrational numbers are all those real numbers that can not be written as the ratio of two positive or negative integers. Such numbers cannot be written as simple fractions of the form p/q, where q must not be equal to 0.
Now, a quadratic irrational is called irrational because of the solution of a quadratic whose rational coefficients are not reducible over the rational numerals. A fractional quadratic will have fractional coefficients, which can be eliminated by taking the product with the least expected denominator.
Since a quadratic irrational is a subset with 2nd–degree algebraic numerical, it can be expressed as:
\[ \dfrac{a + b\sqrt{c}}{d}\]
Solved Example
For the given equation, write it down in standard form and draw a graph of the function while pointing out its zeros.
f(x) = x2 – 6x + 7
Solution
Completing Squares of the function by adding and subtracting 9:
= (x2 – 6x + 9 – 9) + 7
We get a perfect square namely (x – 3)2, such that:
f(x) = (x – 3)2 – 2
This is the standard form of the function f.
From the above equation, we can easily figure out the vertex of the function that is (3, -2).
In order to find the zeros, we must first set the function equal to 0 and take the square root to find the values of x:
= (x – 3)2 – 2=0
(x-3)2 = 2
x – 3 = $\sqrt{2}$
x = 3 $\pm\sqrt{2}$
The last step is to sketch the graph of the standard function by shifting the graph in the first quadrant, i.e., 3 units in the positive x direction and 2 units in the negative y direction.
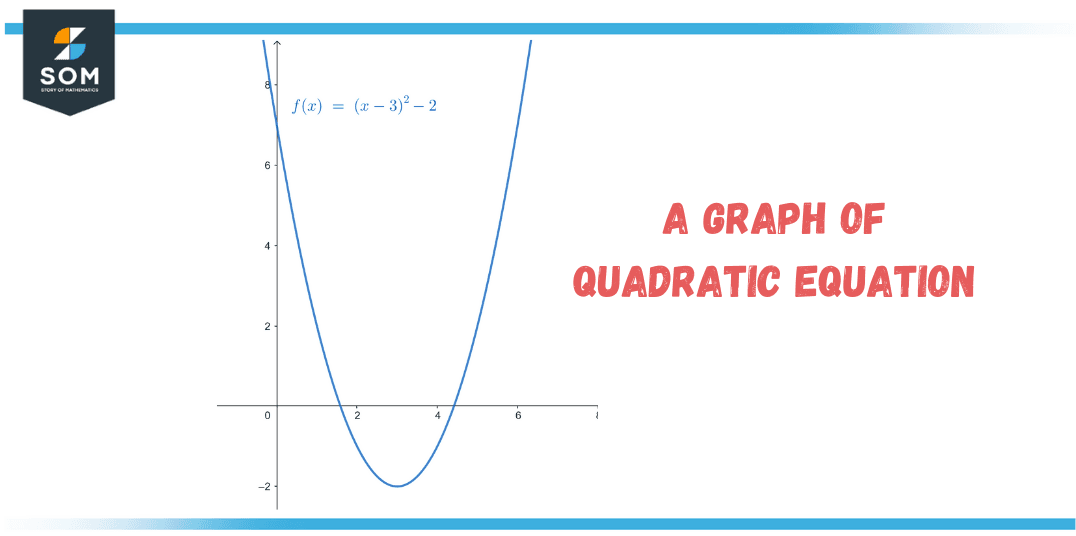
Figure 4 – Graph of the quadratic equation x2 – 6x + 7
If, in any case, the coefficient of x2 is not equal to 1. Then, the first priority is to factorize it before moving forward.
All images were created with GeoGebra.
