JUMP TO TOPIC
Monic Polynomial|Definition & Meaning
Definition
A monic polynomial is a one-variable polynomial with the coefficient of the highest power variable equal to one. In other words, it is a univariate polynomial with a leading coefficient as one.
Figure 1 shows a monic polynomial with four terms.
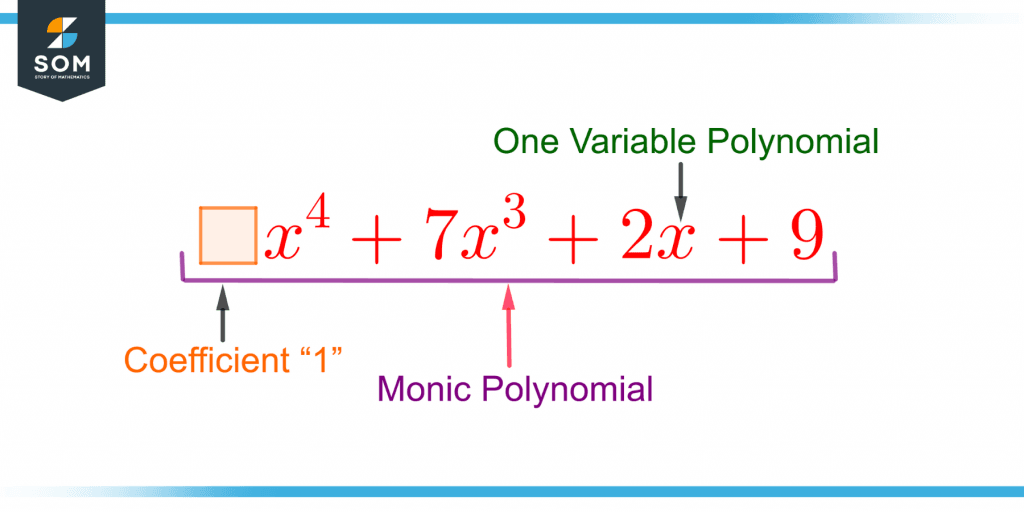
Figure 1 – Demonstration of a Monic Polynomial
The degree of the above polynomial is four. Notice that it is only a one-variable “x” polynomial with the variable’s coefficient of the highest power “four” equal to one, making it monic.
Both conditions must be fulfilled for a polynomial to be monic. Figure 2 shows two polynomials.

Figure 2 – Demonstration of Two Non-monic Polynomials
The first polynomial is not monic because it is a two-variable polynomial of a and b. The second polynomial is a one-variable polynomial of variable m but it is also not monic as the coefficient of the highest power variable is three not one.
Types of Monic Polynomial
A polynomial is an expression consisting of variables, constants, and exponents combined using math operators. The word “poly” means “many”, hence a polynomial has one or more than one term.
The types of monic polynomials include the monic binomial and the trinomial.
Monic Binomial
A binomial is a polynomial consisting of two terms. A monic binomial is a one-variable polynomial having two terms with the leading coefficient as one. For example, the following equation consists of a monic binomial.
x2 – 3x = 0
The degree of this monic binomial is 2. This equation can be solved by taking x as common:
x(x – 3) = 0
The above equation can also be written as:
x = 0, x – 3 = 0
x = 0, x = 3
So, the roots of this monic binomial are x = 0 and x = 3. The number of roots of a polynomial depends upon the degree of the polynomial.
Monic Trinomial
A monic trinomial is a univariate polynomial with three terms having the variable’s coefficient of the highest degree equal to one. The following equation has a monic trinomial:
x2 + 6x + 8 = 0
To factor this equation, it can be written as:
x2 + 4x + 2x + 8 = 0
x(x + 4) + 2(x + 4) = 0
Taking (x + 4) as common gives:
(x + 4)(x + 2) = 0
This can be written as:
(x + 4) = 0, (x + 2) = 0
So:
x = -4, x = -2
So, the roots of this monic trinomial equation are -4 and -2.
A quadratic polynomial is a second-degree polynomial consisting of three terms hence it is also a trinomial. The quadratic equation is:
px2 + qx + r = 0
Where:
p ≠ 0
Where p, q, and r are the coefficients of x2, x, and $x0$. For a quadratic equation to be monic, p should be equal to 1.
Figure 3 shows examples of a monic binomial and a trinomial.
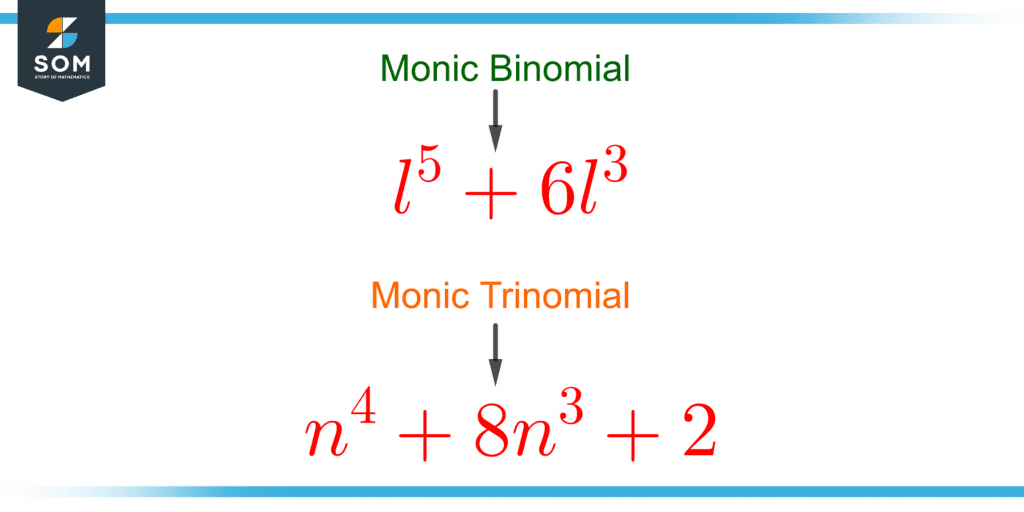
Figure 3 – Examples of Monic Binomial and Monic Trinomial
Monic Polynomials With Different Degrees
The degree of a polynomial is the highest power of the variable in the polynomial. Identifying the degree of a monic polynomial is easier as the variable with the highest degree will have a coefficient of one. Some monic polynomials with different degrees are discussed below:
Monic Polynomial With Degree Three
The polynomial x3 + 2x2 + 4x + 1 is a monic polynomial with degree 3.
Monic Polynomial With Degree Four
The polynomial 5t2 + t4 + 5 is a variable “t” monic polynomial with degree 4.
Monic Polynomial With Degree Five
The polynomial s5 + 2s4 + 7s + 6 is a monic polynomial with variable s having degree 5.
Conversion of a Non-Monic Polynomial Into a Monic Polynomial
A non-monic polynomial can be converted into a monic polynomial by dividing the whole polynomial by the integer multiplied by the highest power variable. For this conversion, the polynomial must be a single variable polynomial.
For example, a non-monic polynomial is given as:
P(n) = 5n4 + 35n3 + 10n
It is a degree 4 non-monic trinomial with a single variable n. It can be converted to a monic polynomial by dividing it by 5, so the polynomial becomes:
P(n) = n4 + 7n3 + 2n
Figure 4 shows the conversion of a non-monic polynomial into a monic polynomial.
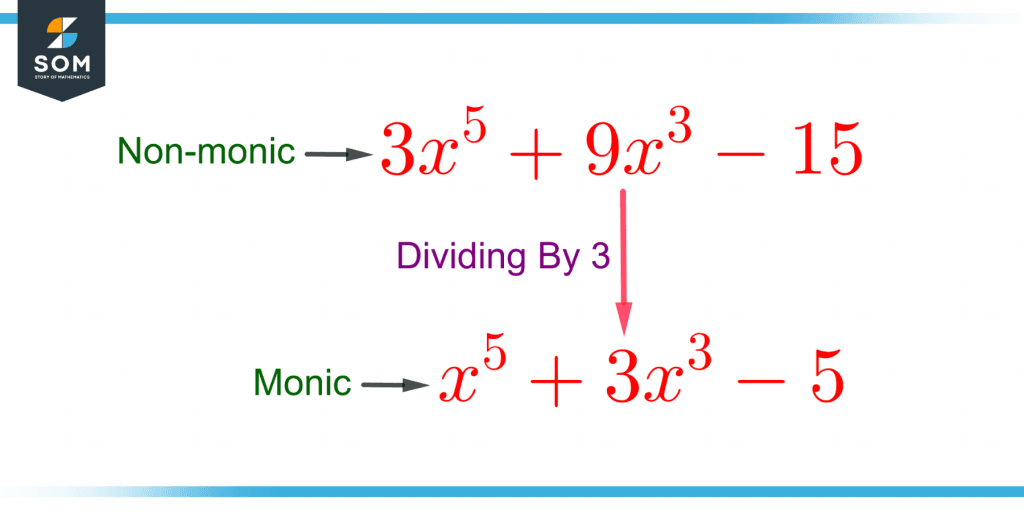
Figure 4 – Conversion of a Non-monic Polynomial into a Monic Polynomial
Properties of Monic Polynomial
A monic polynomial has the following important characteristics.
Product of Monic Polynomials
The product of two monic polynomials is also a monic polynomial provided that both have the same variable. For example, the product P(m) of R(m) = m4 + 2m3 + 3 and Q(m) = m2 + 7 is:
R(m).Q(m) = (m4 + 2m3 – 3)(m2 + 7)
P(m) = m6 + 7m4 + 2m5 + 14m3 – 3m2 – 21
P(m) = m6 + 2m5 + 7m4 + 14m3 – 3m2 – 21
Hence, P(m) is also a monic polynomial of degree 6.
Roots of a Monic Polynomial
The roots of a polynomial are the solutions or the values of the variables for which the polynomial is equal to zero. If a monic polynomial has all the coefficients as integers, then its roots will also be integers.
For example, the monic polynomial x2 + 8x + 16 is solved by using the formula:
(a + b)2 = a2 + 2ab + b2
(x)2 + 2(x)(4) + (4)2 = 0
(x + 4)2 = 0
It can be written as:
(x + 4) = 0, (x + 4) = 0
x = -4, x = -4
Hence, the roots of the polynomial x2 + 8x + 16 with integer coefficients are also integers.
Example
Which of the following is a monic polynomial?
(a) x2 + 2y – 3
(b) y2 + y – 42
Is the monic polynomial binomial or a trinomial? What is its degree? Also, find its roots.
Solution
The polynomial (a) is a two-variable polynomial hence it is not a monic polynomial.
Polynomial (b) is a monic polynomial. It is a trinomial with a degree of 2. The roots of the polynomial can be found by equating it to zero as:
y2 + y – 42 = 0
It can be solved by factorization as:
y2 + 7y – 6y – 42 = 0
y(y + 7) – 6(y + 7) = 0
Taking (y + 7) as common:
(y + 7)(y – 6) = 0
So:
(y + 7) = 0, (y – 6) = 0
y = -7, y = 6
So, the roots of the monic polynomial y2 + y – 42 are 6 and -7.
All the images are created using GeoGebra.
