Quadratic Equation|Definition & Meaning

What Is a Quadratic Equation? 

An equation of the second degree in algebra that involves the variable x is called a quadratic equation. The equation for a quadratic in its simplified form reads as follows: ax² + bx + c = 0. Here, a and b represent the coefficients, x represents the variable, and c represents the constant term.

A non-zero value for the coefficient of x² is required as the first requirement for an equation to be considered a quadratic equation (a value greater than 0). The order in which these terms are written is essential. In most situations, the numerical values of a, b, and c are not expressed as fractions or decimals; instead, they are written as integral values.

You will need to convert all of these equations into the conventional form of the quadratic equation.

The Characteristics of the Quadratic Equation’s Roots

The letters alpha (α) and beta (β) are the standard symbols to indicate a quadratic equation’s roots.

In this section, we will delve deeper into the process of discovering the characteristics of the roots of a quadratic equation, even though we won’t be solving the equation.

In addition, we will read out the formulas that can be used to get the sum and product of the equation’s roots.

It is possible to determine the characteristics of the roots of an equation without locating the equation’s roots (x, y). It is feasible to accomplish this by calculating the value of the discriminant, which is a component of the formula used to calculate the quadratic equation. Based on the discriminant value, it is possible to forecast the characteristics of the roots of the quadratic equation.

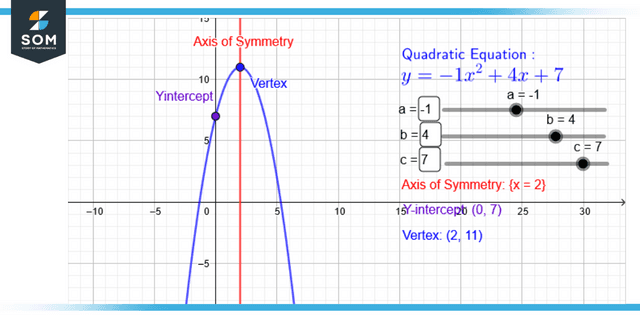
Figure 1: Representation of characteristics of quadratic equation through graph.

Roots of the Quadratic Equation and Their Product

To Determine the sum and product of the roots of a quadratic equation requires the usage of the coefficient of x². These are all helpful pieces of information. It is possible to directly calculate the addition and multiplication of the roots of a quadratic equation by using the equation itself. This eliminates the need to identify the solutions of the quadratic equation.

The quadratic equation has a solution whose roots add up to a number equal to the inverse of the product of the coefficient of x and the coefficient of x². When divided by the coefficient of the x² variable, the constant term answers that the product of the equation’s root is equivalent.

The following is the sum and product of the roots for the quadratic equation ax² + bx + c = 0, which can be written as:

The Total of the Roots: α + β = -b/a = -(coefficient of x / coefficient of x²)

The Roots’ Product: x² = c/a = constant term / coefficient of x²

It is also possible to formulate the quadratic equation using the roots of the given equation.

Various Approaches to the Resolution of Quadratic Equations

The two possible values of x that result from solving a quadratic equation can also be thought of as the problem’s two roots. There are four distinct approaches to resolving the problem of locating the roots of a quadratic equation. The following is a rundown of the four different approaches to solving quadratic equations:

• The process of factoring the quadratic equation
• Using the quadratic formula (which we have seen already)
• The Completion of the Square Graphing Method to Locate the Roots

The above-mentioned approaches to understanding how to apply these methods and their uses and applications.

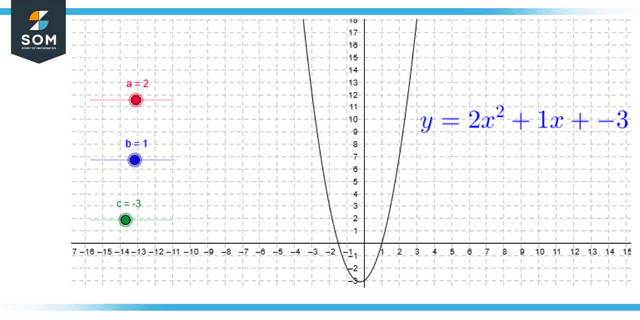
Figure 2: Representation of quadratic equation

Factoring the Quadratic Equation

Factorising a quadratic equation involves going through a series of phases. To obtain a general form of the quadratic equation ax² + bx + c = 0, we need to begin by separating the central component into two parts so that the product of the terms is equivalent to the constant term.

In addition, we can derive the necessary factors by extracting the common denominators from the set of denominators that are accessible.

Graphing an Equation With Quadratic Terms

It is possible to generate the graphing of the quadratic equation ax² + bx + c = 0 by first describing the quadratic equation as a function, which looks like this: y = ax² + bx + c.

When we continue to solve the problem and substitute values for x, we can obtain values for y, which in turn allows us to obtain a large number of points. It is possible to generate a graph for the quadratic equation in the shape of a parabola by presenting these points along the coordinate axis.

Important Points Regarding Quadratic Equation

Some of the hints and strategies regarding quadratic equations that are provided below help simplify the process of solving quadratic equations.

• In most cases, the quadratic equations can be solved using the technique of On the other hand; the quadratic formula is utilized in situations where the problem cannot be solved via factorization.
• There is another name for the roots of a quadratic equation: the zeroes of the equation.
• When the discriminant value of a quadratic equation is negative, the roots of the equation are expressed by complex numbers.

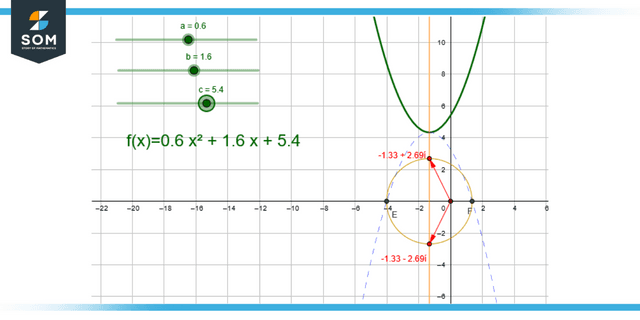
Figure 3: Representation of complex roots of quadratic equation

Example Problems of Quadratic Equations

Example 1

Find the roots of the given equation:

-2x² + 46x + 100 = -5x² + 6x

Solution

-2x² + 46x + 100 + 5x² – 6x

3x² + 40x + 100 = 0

Now, by applying the quadratic equation, we will get the roots:

x = -10/3 , x = -10

Example 2

Solve the following equation by completing the square:

-2x² + 4x – 6 = 0

Solution

-2 (x² – 2x) – 6 = 0

Now we will add positive and negative 1:

-2 (x² – 2x + 1 – 1) – 6 = 0

-2 (x² – 2x + 1) + 2 – 6 = 0

-2 (x – 1)² – 4 = 0

All images/graphs are created using GeoGebra.

Quadratic Definition < Glossary Index > Quadrillion Definition