Quarter|Definition & Meaning

A quarter can indeed be thought of as one portion out of four total portions that are equal in size. If we look at one full unit, we can see that it is composed of four quarters. 

In mathematics, the number quarter is represented via the use of fractions. A quarter fraction can be defined as the split of one whole into four equal parts. In this context, the number 1 refers to the part that is being discussed, and the number 4 refers to the number of parts that have been created by the division of the whole.

It is expressed as 1/4 when written out in the numerical form.

The following figures graphically represent different quarters.

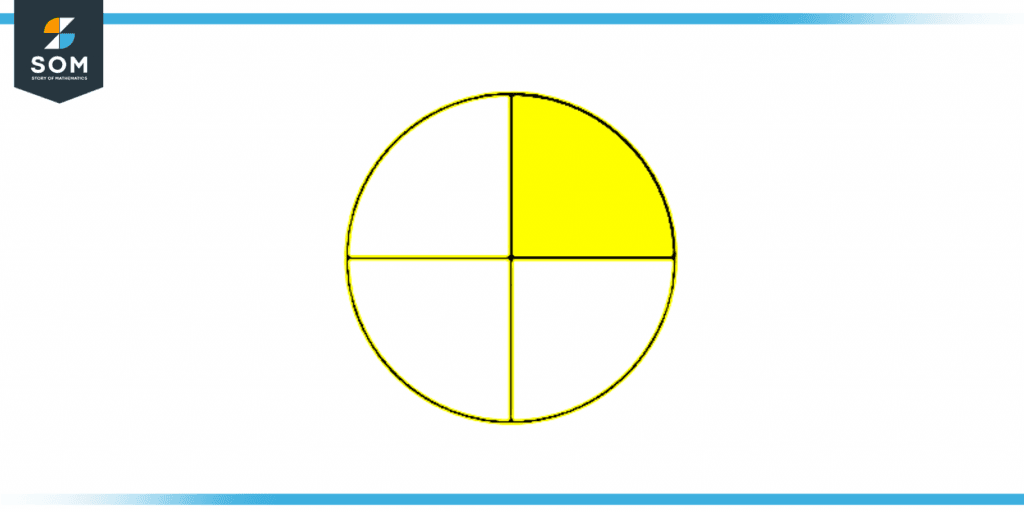
Figure 1 – Representation of 1 quarter

What Exactly Is a Quarter?

One quarter indicates one among four equal pieces. As an example, a family consists of four people in total. You cut the pizza into four equal pieces, and you give each member the same amount of each piece. One quarter is the name given to each of the four sections that result whenever a whole is cut into quarters of equal size.

What Does It Mean To Have Two Quarters?

Two quarters are equal to two of the four parts total. Imagine that you cut the pizza into four equal portions and that you have two pieces of pizza left over. When read aloud, the number 24 might be interpreted as either two-quarters or two-fourths.

The figure below represents two quarters.

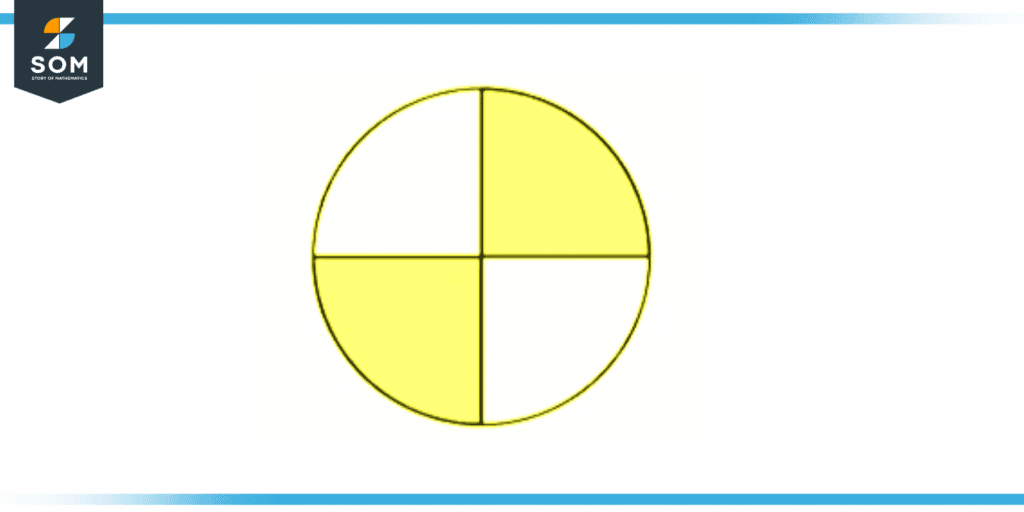
Figure 2 – Representation of quarters

What Does It Mean To Have Three Quarters?

The term “three-quarters” refers to three of the four equally sized components. When you see the number 34, you should read it as “three-quarters” or “three-fourths.”Imagine you cut the pizza into four equal pieces, and there are still three slices of pizza left behind.

In summing up, a quarter can be thought of as one of the four equal parts that anything is divided into. Additionally, the term “two quarters” refers to the division of a whole into two equal halves, while “three quarters” refers to the division of a whole into three equal parts.

Example of Quarter

To further comprehend what a quarter is in terms of numbers, let’s look at an example. For instance, in order to calculate the quantity of a quarter of 8 peaches, you must first divide the peaches into 4 equal parts. Each portion will include a total of two peaches. Each equal part is representative of a quarter of the whole. Therefore, a quarter of eight is equal to 2.

The following figure represents the whole circle in 4 quarters.

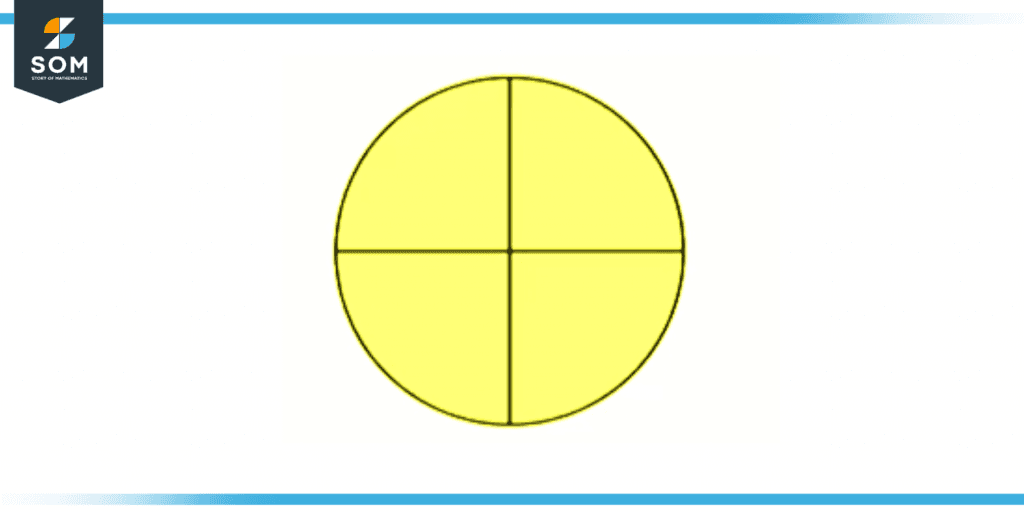
Figure 3 – Representation of 4 quarters

Utilizing Quarters in a Number of Different Forms

In mathematics, a quarter can stand for a number of different things, including the following:

The passage of time, for example, one-quarter of such an hour. One hour, or 60 minutes, can be divided into four equal parts using this method. One quarter is equal to fifteen minutes in length. As a result, the times 3:45 and 4:15 are indicated when the phrases “quarter to 4″ and “quarter past 4” are used, respectively.

The year, or a portion of the year, like a quarter. One year, which consists of 12 months, can be divided into four (a quarter). This indicates that there are three months in each quarter.

• The first quarter runs from January 1st to March 31st.
• The second quarter runs from 1 April to 30 June.
• The third fiscal quarter runs from July 1 through September 30.
• The fourth quarter runs from October 1st to December 31st.

The amount of money in question, like a quarter of such a dollar. 100 pennies make 1 dollar. Therefore, the value of a quarter of such a dollar is equal to 25 cents.

Another one of McDonald’s most popular burgers is called the “Quarter Pounder,” which similarly uses the term quarter as its moniker. The fact that the burger patty, in its uncooked state, weighs one-fourth of a pound led to the creation of this particular name for the dish.

Numerical Example of Quarter

Express the following numbers in terms of one quarter.

1. 40
2. 24
3. 12
4. 8
5. 16
6. 28
7. 4
8. 44
9. 48

Solution

The given values are:

40, 24, 12, 8, 16, 28, 4, 44 and 48

We have to find the quarter for the given values.

We know that a quarter is equal to 1/4.

1. 40 divided by 4 results in  10, so the value of the quarter is 10.
2. 24 divided by 4 results in  6, so the value of the quarter is 6.
3. 12 divided by 4 results in  3, so the value of the quarter is 3.
4. 8 divided by 4 results in  2, so the value of the quarter is 2.
5. 16 divided by 4 results in  4, so the value of the quarter is 4.
6. 28 divided by 4 results in  7, so the value of the quarter is 7.
7. 4 divided by 4 results in  1, so the value of the quarter is 1.
8. 44 divided by 4 results in  11, so the value of the quarter is 11.
9. 48 divided by 4 results in  12, so the value of the quarter is 12.

Hence, we have found the values of quarters for the given values.

All images were created with GeoGebra.

Quantity Definition < Glossary Index > Quintillion Definition