JUMP TO TOPIC
Radian|Definition & Meaning
Definition
A radian equals the angle subtended on the circle’s center by an arc whose length equals the circle’s radius. In degrees, a radian equals (180/$\pi$) $\approx$ 57.2958 degrees. If you consider a sector OAB on a circle where O is the center and AB is the arc such that |arc AB| = r, then $\angle$AOB = $\angle$BOA = 1 radian.
Figure 1 below shows a radian.
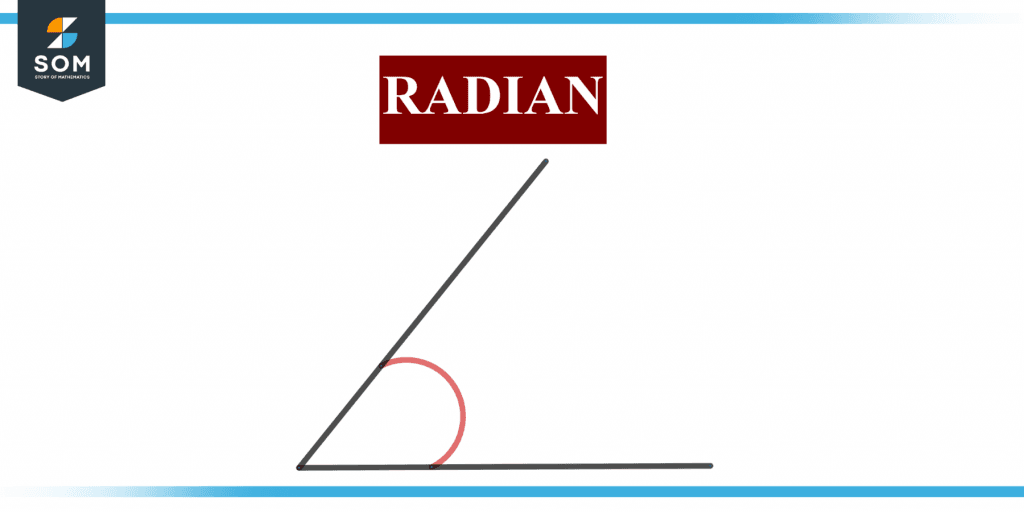
Figure 1 – Representation of a radian.
A radian is defined as the arc subtended at its center by a one-unit-long arc within a line segment “rad” is the radian measurement’s symbol. So because the width of a circle having radius “r” = 2r, the diameter of something like a circle to radius “r” is 2.
Consequently, one full circle of the initial side yields a 2-radian angle. Furthermore, in a circle of radius r, an arc of width r disrupts an arc of 1 radian, a plane angular measuring unit equal to something like an angle at the center of a circle distanced by an arc whose length matches the radius or 57.3 degrees.
Figure 2 below shows the radian measure of a circle.
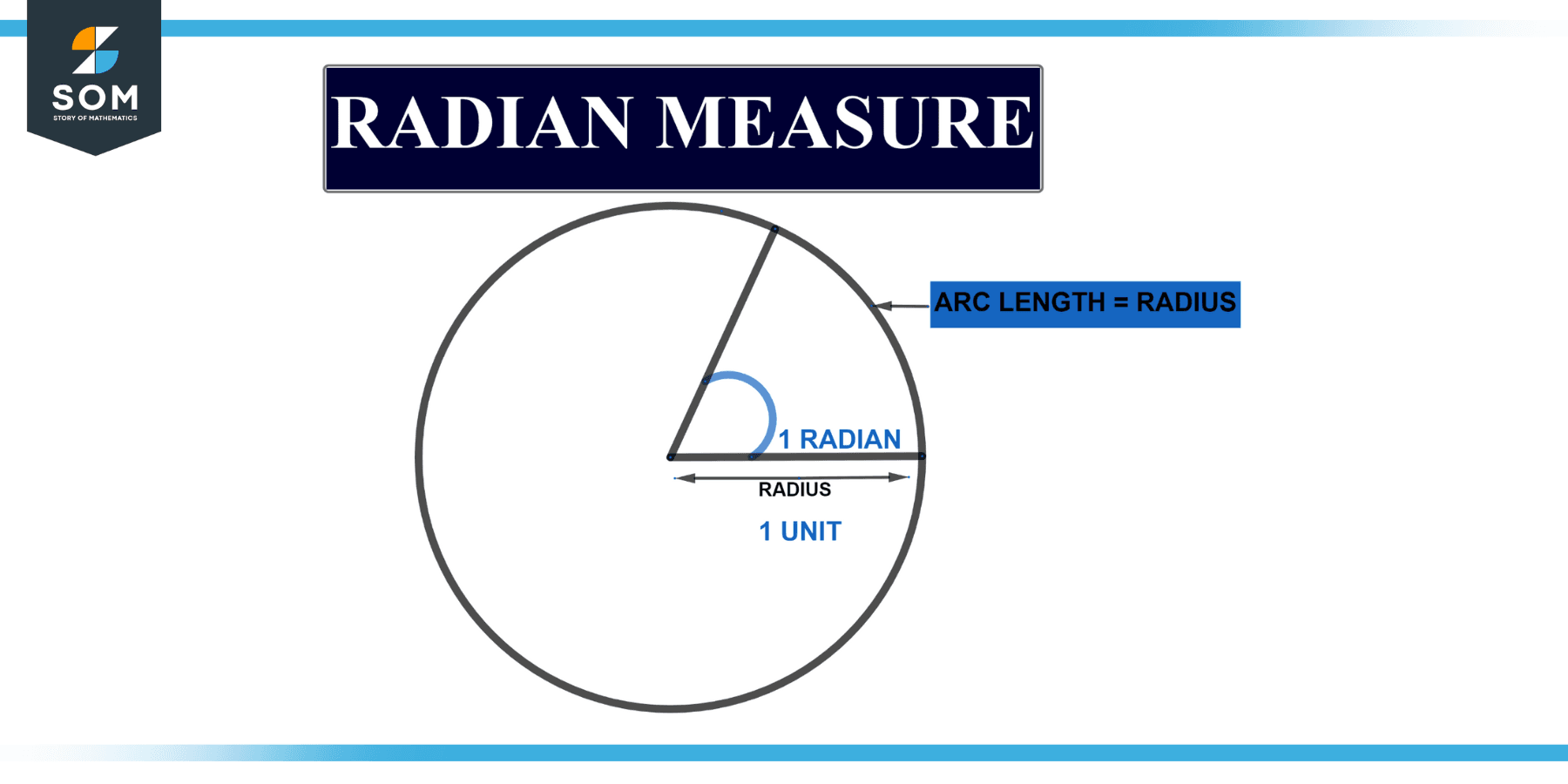
Figure 2 – Representation of measuring a radian
What Is Radian?
A radian is indeed a unit of measurement for angles. Angles are measured using two units: degrees and radians. You may have used degrees to measure the overall sizes of angles up to this point. Angle measurements in advanced mathematics, on the other hand, are typically defined using a unit system other than the degree system for several reasons. The radian system is the name given to this system.
- “Radian” is an angle measuring unit. Here are some interesting facts about “radian.”
- Radian is represented by the letter “rad” or the symbol “c” inside the exponent.
- If an angle is expressed without units, it is written in radians.
What Makes Radian Unique?
Radians allow you to connect a linear measurement to an angle measurement. A unit circle consists of a radius of one unit. One unit all-along circumference equals one unit all-along radius. Wrap an anticlockwise number line around a unit circle, beginning at zero (1, 0).
Uses of Radian
- In calculus and most other fields of mathematics, angles are measured in radians.
- Radians are very commonly employed in physics. When doing angular measurements in physics, they are preferable over degrees.
Formula for Radian
We already know that 1 radian equals the angle formed by the arc of even a circle, where length equals the radius of that circle. Therefore, the angle area enclosed by such an arc of radians of the circle is described as the arc-to-circle radius ratio.
\[\theta =\frac{\text{arc length}}{\text{radius}}\]
If we consider the arc to be the entire circumference of the circle, then circular length = $2\pi r$. We also understand that the diameter of a sphere at its center forms a 360-degree angle; using the calculation mentioned above, the radian formula is 2$\pi$ equals 360 degrees.
Degrees
A degree is the unit of measurement for angles. It isn’t a SI unit since radians are the SI magnitude of angles. A protractor is used in geometry to identify the angle of degrees. A protractor is widely used in the classroom to measure angles to solve math problems. Let’s look at how the degree sign represents an angle measurement.
A degree is a measurement unit used to express an angle’s measure. Angles are usually measured using two units of measurement: radians and degrees. In practical geometry, the angle is always measured in degrees. The sign for a degree is °. (degree symbol). A complete angle of degrees equals 360 degrees (sometimes written as 360°), equal to one entire revolution.
Conversion of Radian to Degrees
An angle could be converted between “radians to degrees” or “degrees to radians” as needed. For these conversions, we utilize the radian calculation 2$\pi$ = 360 degrees.
Radian to Degrees Conversion
The radian formula is as follows:
2$\pi$ = 360 degrees
As a result, we get:
1 Radian = $\dfrac{360 \text{ degrees}}{2\pi \text{ radians}}$ = $\dfrac{180 \text{ degrees}}{\pi \text{ radians}}$
To convert from radians to degrees, multiply that angle by $\frac{180}{\pi}$. Equivalently, divide it by $\frac{\pi}{180}$. This is a method for converting radians to degrees.
The Degree to Radian Conversion
The radian formula is as follows:
2$\pi$ = 360 degrees
As a result:
1 Degree = $\dfrac{2\pi \text{ radian}}{360 \text{ degrees}}$ = $\dfrac{\pi \text{ radians}}{180 \text{ degrees}}$
To convert from degrees to radians, multiply that angle by $\frac{\pi}{180}$. Equivalently, divide it by $\frac{180}{\pi}$. This is a straightforward method for converting degrees to radians.
Figure 3 below shows the conversion of radians to degrees and vice versa.
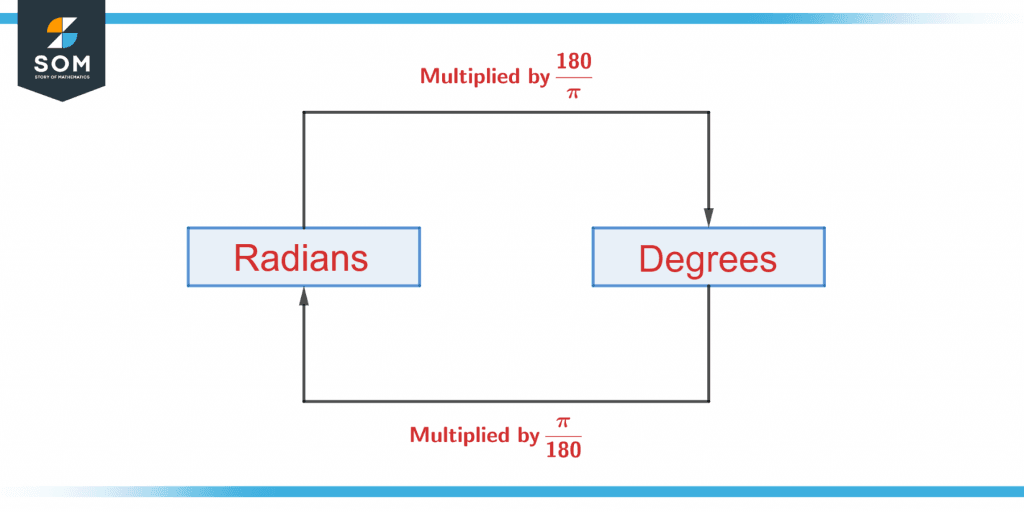
Figure 3 – Conversion of radian to a degree.
Example Problems Using Radians
Below are some examples of radian which would help further clarify your understanding of the topic.
Example 1
What’s the size of a circle with a radius of 6 inches and an angle of 1.5 radians?
Solution
The circle’s radius is 6 inches.
The arc’s subtended angle equals 1.5 radians.
The distance is defined as the combination of the radius and the angle area enclosed by the arc just at the circle’s center.
As a result, the arc length is (6)(1.5), which equals 9 inches.
The length of the arc is 9 inches.
Example 2
What is the diameter of a circle with a radius of 6 inches and an angle of 2.5 degrees?
Solution
The circle’s radius is 6 inches.
An arc’s subtended angle is equal to 2.5 radians.
The distance is calculated by adding the radius and angle area encompassed by the arc directly in the center of the circle.
As a result, the length is (6)(2.5) = 15 inches.
The length of the arc is 15 inches.
Example 3
What is the diameter of a circle with a radius of 7 inches and an angle of 2.5 degrees?
Solution
The circle’s radius is 6 inches.
An arc’s subtended angle is equal to 2.5 radians.
The distance is calculated by adding the radius and, thus, the angle area encompassed by the arc directly in the center of a circle.
As a result, the length is (7)(2.5), equaling 17.5 inches.
The length of the arc is, therefore, 17.5 inches.
All Images are made using GeoGebra.
