JUMP TO TOPIC
Radical|Definition & Meaning
Definition
The general term for the nth root of a value or expression. The symbol for the radical is $\sqrt{}$, usually used as $\sqrt[n]{a}$, where n is the index and a is the radicand. For example, the term $\sqrt[4]{16}$ represents the quadruple root (or 4th root) of the number 16 (the radicand), which equals two since 2$^4$ = 16.
In mathematics, the symbol for a radical is the under-root, which is also known as the root sign.
A radical is indeed the inverse of an exponent. It may represent a square root or cube root, and the number that comes before the sign or radical is referred to as the degree or index number. This number, a complete number rendered as an exponent, eliminates the radical previously there.
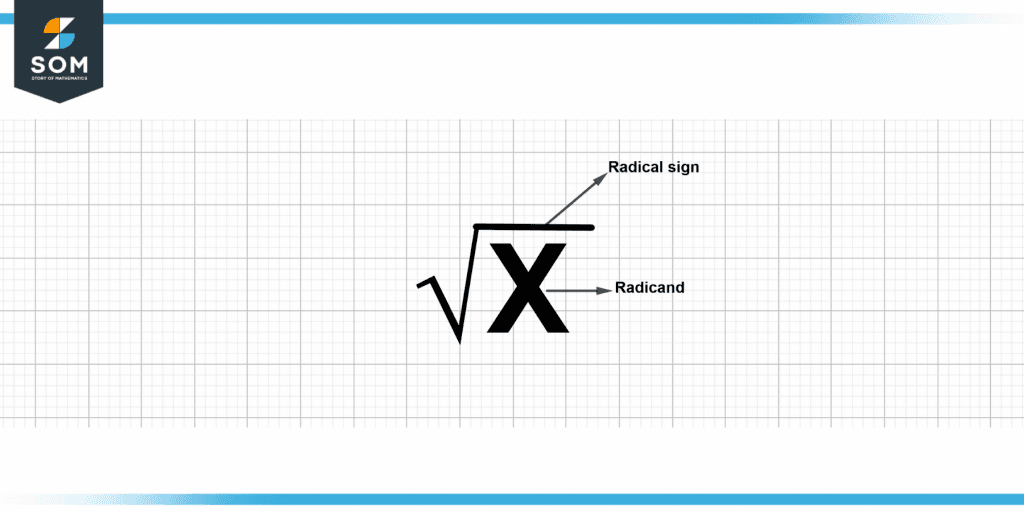
Figure 1 – Radical representation
What Exactly Does the Term Radical Mean?
There is no difference between a number’s radical and its root; they are the same thing. It’s possible that the root is just a square root, a cube root, or even just an nth root. As a result, a radical is a name given to any number or phrase that makes use of a root.
The English word “radical” originates from the Latin term “radix,” which literally translates to “root.” The term “radical” can be used to refer to a variety of distinct roots for a number, such as the square root, the cube root, the fourth root, and on.
The number that comes even before radical is called the number index or degree, which has a specific meaning. Multiplying this number by itself this many times gives us the answer to how many times we need to multiply the radical by this number.
This is seen as the counterpart of an exponent, much in the same way as addition is the contrary of subtraction & division is the opponent of multiplication.
Representation of Radical
A radical is represented by the symbol as √. A radical is also related to the following terms:
A radical equation involves the variable inside a radical.
The term “radical expression” refers to an expression that is contained within a square root.
The term “radical inequality” refers to an inequality that is contained within a radical.
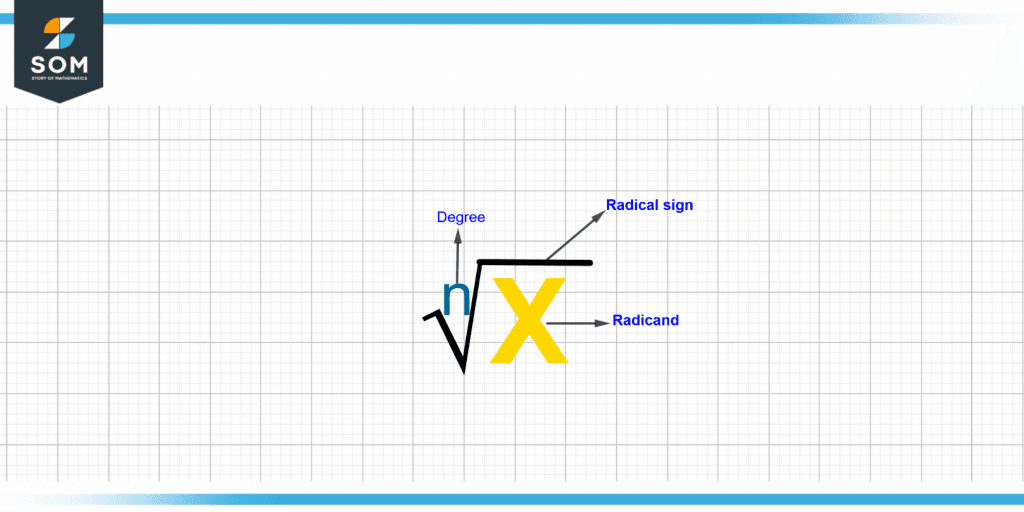
Figure 2 – Complete representation of radical
The illustration below represents the 4 in terms of the radical sign.
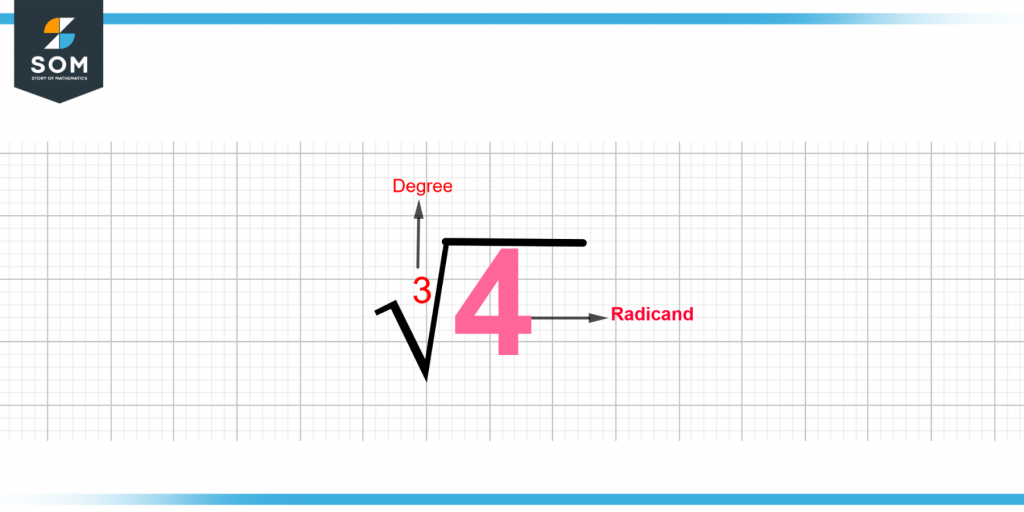
Figure 3 – Representation of 4 in terms of radical
Basic Radical Principles
The following are some broad guidelines to follow if you identify as a radical:
If the number that is being radicalized has a positive value, then the result will also have a positive value.
If the number that is being subtracted by the radical is negative, then the outcome will also be negative.
Irrational numbers are produced whenever the number underneath the radical equals negative, and also, an index is an even integer. This combination produces an irrational outcome.
The value of the radical will equal the square root if an index also isn’t specified.
It is possible to multiply numbers with identical radicals and indices.
For numbers that fall under the same radical, the division is possible.
When the number is divided under the same radical, the multiplication rule can be applied in the other direction.
In any equation, the radical can also be expressed in its exponent form.
The radical expression itself is equal to the radical’s inverse exponent, which is the index number.
The Radical Formula
In order to get a solution for an equation containing radicals, it must first be made radical-free. We have to power both of the equation’s sides with n in order to make an equation involving the nth root radical free. This made the radical equation free of radicals more difficult to see. Let’s take a look at the radical formula that’s down here.
\[n\sqrt{x} = p\]
\[x^\frac{1}{n} = p \]
\[(x^\frac{1}{n})^n = p^n \]
\[x = p^n\]
- The value ‘n’ is referred to as the index.
- The term “radical” refers to the expression as well as a variable that is located within the radical sign, which in this case is the letter x.
Application of Radical in Real Life
In addition to their usage in a wide number of mathematical applications, radicals also have a great many applications in the real world. The following are some examples:
When it comes to the solution of equations, radicals can be utilized to solve equations that contain roots.
Radicals are frequently employed in geometry to determine a line segment’s length or a shape’s area.
Radicals are utilized in a variety of scientific and engineering domains in order to find solutions to challenges involving a range of dimensions and quantities.
In the field of computing, radicals are used for operations on various data structures and algorithms.
In summary, radicals have several practical applications in diverse domains of mathematics, physics, engineering, and computer programming. These applications can be found in a wide variety of contexts. Equations are solved with them, dimensions and quantities are determined with them, and statistical measurements are computed with them.
Summary
A mathematical expression or a number can be represented by the symbol known as a radical, which stands for the expression’s or number’s root. The symbol for it is termed as a radical sign and represented by √. As an illustration, the square-root of 9 is written as the symbol 9, and even the 27 cube root is written as the symbol $\sqrt{27}$.
Radicals can be employed to symbolize either positive or negative roots, depending on the context. For instance, the four square root is two, and the negative four square root is a negative four raised to the power minus four, which is equivalent to two imaginary units.
Simplifying radicals can be accomplished by relocating any components that were previously located within the radical sign to a new location outside of the radical sign in the form of a coefficient.
A Numerical Example of Radical
Example 1
Write the given number in terms of radical
\[3^{\frac{6}{2}}\]
Solution
Given that:
\[3^{\frac{6}{2}}\]
We have to write it in radical form.
So:
\[3^{\frac{6}{2}} = (3^6)^{\frac{1}{2}}\]
\[3^{\frac{6}{2}} = 729^{\frac{1}{2}}\]
\[3^{\frac{6}{2}} = \sqrt{729}\]
Example 2
Write the given number in terms of radical
\[3^{\frac{8}{2}}\]
Solution
Given that:
\[3^{\frac{8}{2}}\]
We have to write it in radical form.
So:
\[3^{\frac{8}{2}} = (3^8)^{\frac{1}{2}}\]
\[3^{\frac{8}{2}} = 6561^{\frac{1}{2}}\]
\[3^{\frac{8}{2}} = \sqrt{6561}\]
Example 3
Write the given number in terms of radical
\[3^{\frac{7}{2}}\]
Solution
Given that:
\[3^{\frac{7}{2}}\]
We have to write it in radical form.
So:
\[3^{\frac{7}{2}} = (3^7)^{\frac{1}{2}} \]
\[3^{\frac{7}{2}} = 2187^{\frac{1}{2}} \]
\[3^{\frac{7}{2}} = \sqrt{2187} \]
All mathematical drawings and images were created with GeoGebra.
