Radicand|Definition & Meaning

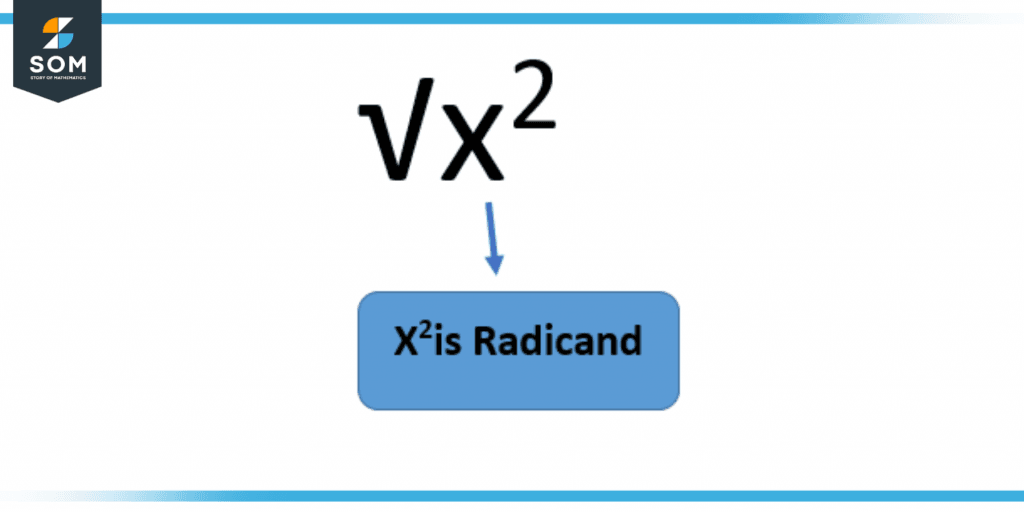
Figure 1 – Radicand x$^2$

In mathematics, the term “radicand” refers to the value or expression that is printed underneath a radical sign or root symbol. It is a way of expressing something from which we are drawing inspiration. Take, for instance, the statement which states the cube root of 64 is 4, as an example. In this case, the radicand is the number 64. 

The Concept of a Number’s Root

Both the word “radicand” and the word “radical” can be traced back to the Latin word “radix,” which literally translates to “root.” The reasoning for this is that the root, in this case, the root of a word, is the source of whatever it is that it is.

If you take the cube or square of a number, whatever number it was originally derived from becomes the root, whereas the number that was squared or cubed itself becomes the radicand.

These phrases made their first appearance in print in England in the middle of the 1600s in a book written by John Pell entitled An Introduction to Algebra.

In mathematics, an expression, number, or variable written inside a root symbol is referred to as a radicand. It is a quantity itself for which we are searching for the underlying cause. When we study exponents and roots, we come across the term “radicand” quite frequently. Therefore, the value of the radicand  4 is equal to 2.

The following are some examples of radicands. Here, x is the radicand:

√x

Here a + b is the radicand:

√(a+b)

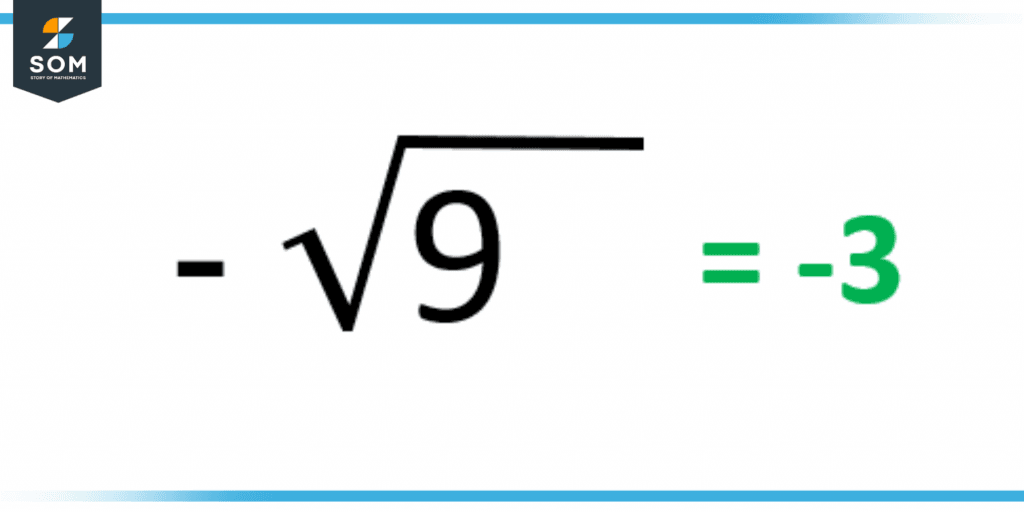
Figure 2 – Negative square root of a radicand

Here is another example where the negative sign is with the square root, so 9 is a perfect square here; the negative sign will come with the answer as it is.

This is the problem that you are attempting to solve by locating the root. The value (3x) in the expression√(3x) serves as the radicand denoted by the symbol (3x).

An equation is said to be radical if it has a minimum of one variable expression inside of a radical, which is often the square root of the variable.

The radical could be any root; for example, the square root or the cube root. In most cases, equations can be solved by separating the variable in question and then undoing whatever changes have been made to that variable.

Radicand and Radical

A sign called the radical (√) is utilized for the purpose of indicating the root of any variable or number. It is written as a symbol. The radicand is the word or expression that is placed just under the radical sign. In other words, the radicand is an input to the radical (or nth root) function.

There is one additional concept that pertains to the radicand, and that concept is called the index. Let’s get some information on it.

Index and Radicand

You must already comprehend the definition of radicand by this point in time. Now, if we look closely at the examples that have been presented here, we will notice that the radicand sign has a small number printed just of it is often a natural number that is bigger than 1.

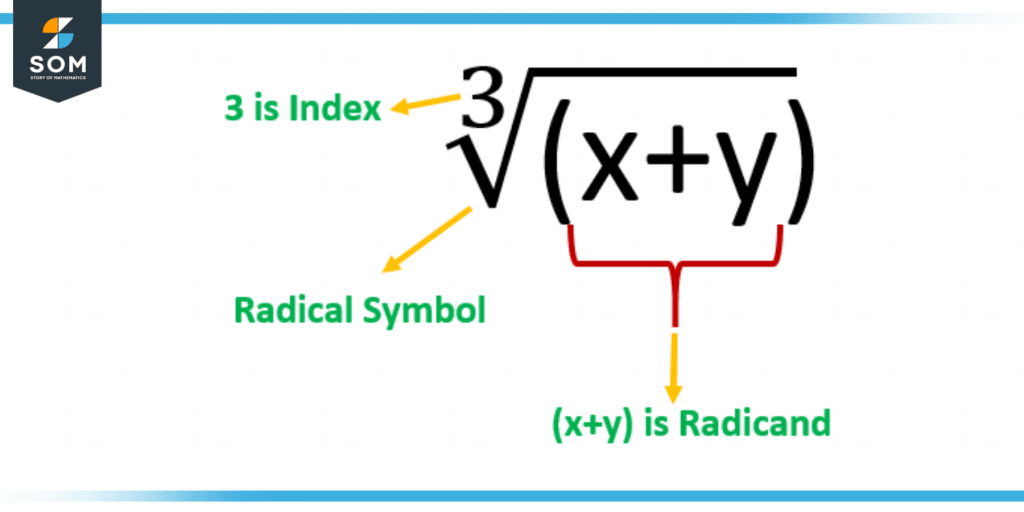
Figure 3 – The index and the radicand

For example, in the expression $\mathsf{\sqrt[3]{x+y}}$, the number 3 is placed on the upper left of a radicand. In mathematics, this type of quantity is called an index. To put it another way, it is the same as the number of the root.

In the event that there is no quantity of index given to a left of a radicand symbol, we take the index to be 2, as this is the default.

When Radicand Is Negative

Principal square roots are obtained by multiplying primary numbers to obtain the radicand, and negative values obtained by multiplying primary numbers to obtain the same positive number are referred to as negative square roots. If we are given a negative number and asked to find the square of that number, there is no real number that can be used.

When Radicand Is a Perfect Square

If the number that is contained within the radical sign, known as the radicand, is a positive number and it is possible to factor it as the squared of another positive integer, therefore the square root of such a number is immediately apparent. The following is a property that we have in this instance:

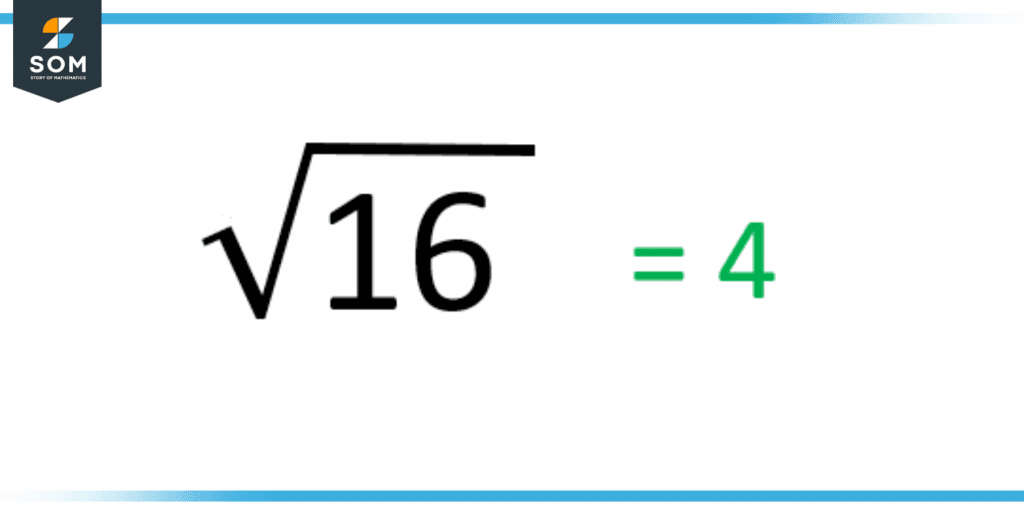
Figure 4 – When the radicand is a perfect square

When Radicand Is Not a Perfect Square

There is no guarantee that the radicand will always take the form of a perfect square. Whenever any positive integer does not have a perfect square, then the square root of that positive integer will be an irrational number. For instance, here in the figure below, 72 is not a perfect square, so the answer is an irrational number.

Still, you can get a pretty good approximation to the nearest square number, leading to the answer in a whole number.

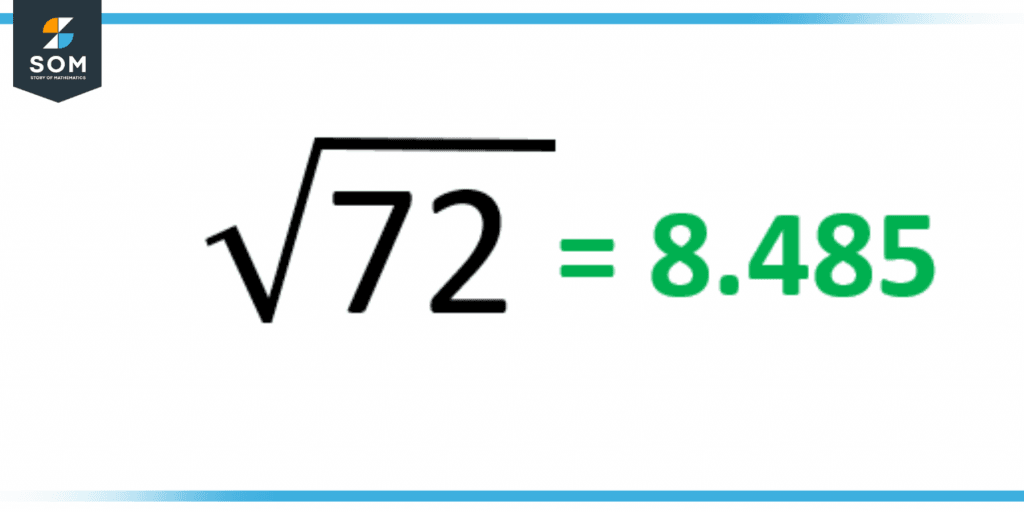
Figure 5 – When the radicand is not a perfect square

Example 1

Solve the following given expression:

√(64) – 5

Solution

Here the square root is of the perfect square that is radicand is 64, which is a perfect square of 8:

 = √(8²) – 5

Here the square will cancel with the square root, so only 8 will be left:

= 8 – 5

= 3

The final answer to the above expression is 3.

Example 2

Identify the radicand  2 + 2√(121) and also solve the following expression.

Solution

The radiant in the given expression is 121. Here, 121 is a perfect square of 11:

121 = 11²

This implies that:

2 + 2√(121) = 2 + 2√(11)²

= 2 + 2(11)

= 2 + 22

= 24

Example 3

Solve the following expression evolving radicand √(3x – 6 )² and find the value of x.

Solution

Here radicand is 3x – 6:

= √(3x – 6 )²

The square root will cancel with the square:

√(3x – 6 )² = 3x – 6

3x = 6

x = 6/3

x = 2

All the figures above are created on GeoGebra.

Radical Definition < Glossary Index > Random Sample Definition