JUMP TO TOPIC
- Definition
- What Is Meant by a Random Sample?
- What Is Random Sampling and Why Is It Used?
- The Four Types of Random Sampling
- What Is the Difference Between Random and Non Random Sampling?
- What Are the Advantages of Random Sampling?
- What Are the Limitations of Random Sampling?
- Three Examples of Random Sample in Mathematics
Random Sample|Definition & Meaning
Definition
A sample that is chosen from a population randomly such that each member of the population has an equal probability of being selected is called a random sample. For example, choosing 2 students from a class of 20 by randomly drawing names from a list is a random sample.
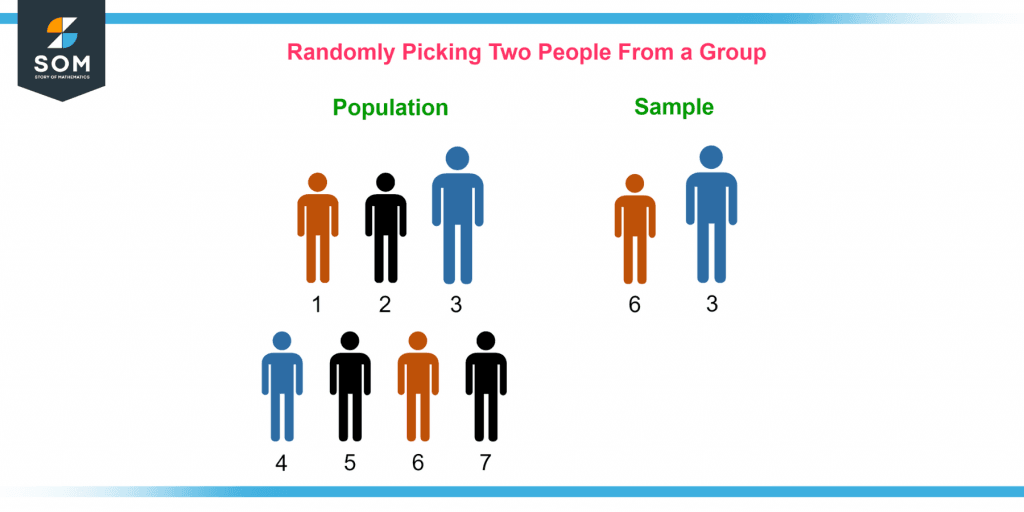
Figure 1 – Random Sampling
What Is Meant by a Random Sample?
A subset of people chosen at random from a broader population has an equal probability of being included in the sample, which is why it is called a random sample.
This reduces the likelihood of selection bias and ensures that the sample accurately and impartially reflects the population. Using this, conclusions may be reached about the population from which the sample was taken.
What Is Random Sampling and Why Is It Used?
The process of choosing a small group of people at random from a larger population ensures that each person has an equal probability of being chosen for the sample. This reduces the possibility of selection bias and guarantees that the sample is representative of the population.
Random sampling is employed in statistics and research to infer the characteristics of a population from a sample. For example, if a sample of 100 individuals is selected randomly from a population of 1,000, and it is found that 10% of the sample has a certain characteristic, it can be inferred that approximately 10% of the population also has that characteristic.
Random sampling is also used in quality control, survey research, and other fields to estimate population parameters and test hypotheses.
It’s important to note that random sampling is just one of many sampling techniques, and it’s not always the best choice for every research or experimentation design. In some cases, other sampling methods, such as stratified, cluster, or systematic sampling, might be more appropriate.
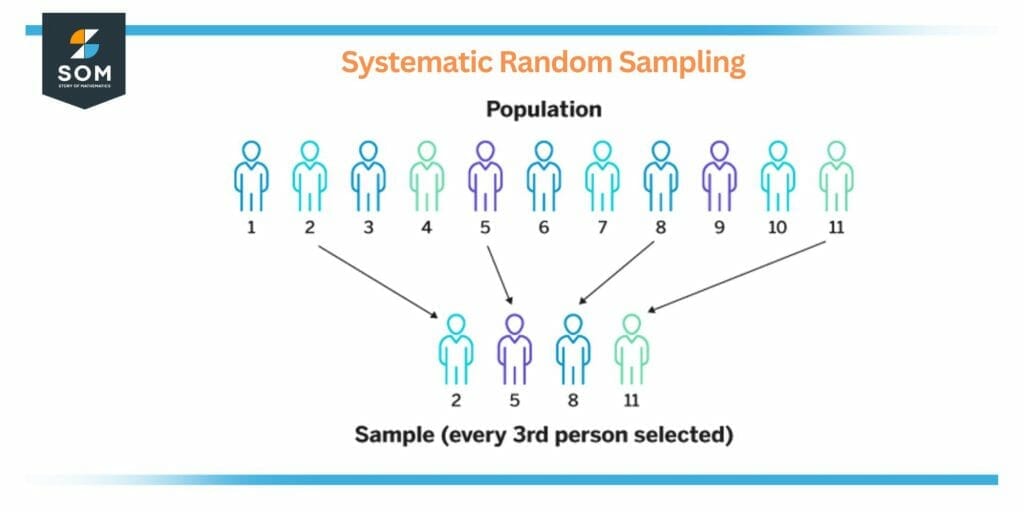
Figure 2 – Systematic Random Group
The Four Types of Random Sampling
There are several types of random sampling techniques, but four of the most commonly used are:
- Simple Random Sampling: In this method, individuals are chosen at random from the population without any bias. Every member of the population, therefore, has an equal chance of being picked as the sample.
- Systematic Sampling: With this approach, people are randomly chosen from the population at regular intervals, like every tenth person. When the population is presented in an organized list, like a phone book or a list of workers, this approach is helpful.
- Stratified Sampling: With this technique, strata or subgroups of the population are created, and random samples are drawn from each one. When the population is diverse, and it’s vital to make sure that various subgroups are represented in the sample, this strategy can be helpful.
- Cluster Sampling: This technique involves grouping the population into clusters and then randomly choosing samples from each cluster. When the population is huge and distributed, and it is neither practical nor cost-effective to poll every person, this strategy is helpful.
It’s crucial to remember that there are several other random sampling techniques, each of which has pros and cons depending on the research design and characteristics of the population being investigated.
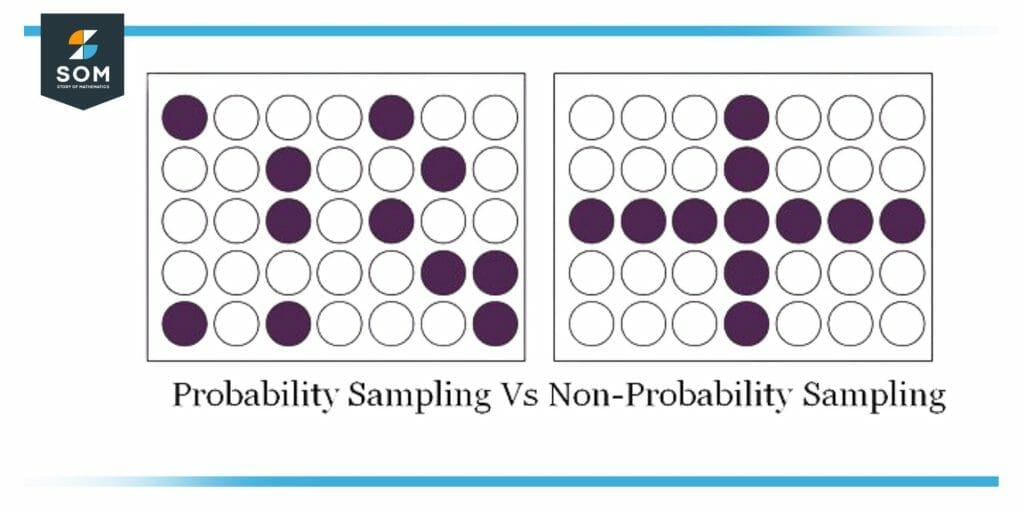
Figure 3 – Random vs. Non-Random
What Is the Difference Between Random and Non Random Sampling?
Random sampling and non-random sampling are two different methods of selecting a sample from a population.
In order to provide every person in the population an equal chance of being included in the sample, random sampling is a technique used to choose a small group of people from a larger population.
This reduces the likelihood of selection bias and ensures that the sample is representative of the population.
On the other hand, non-random sampling is a technique for choosing a sample in which the people are not picked at random. Instead, the sample is chosen using some bias or criterion, such as voluntarism, convenience, or opinion.
This method can introduce bias and lead to a sample that is not representative of the population.
It’s important to note that non-random sampling is not always bad or invalid; it all depends on the research goals and what the sample will be used for.
For instance, a researcher could utilize non-random sampling techniques like convenience sampling if they wish to examine a particular segment of the population, such as illness patients. However, random sampling is typically favored if the objective is to draw conclusions about the population as a whole.
What Are the Advantages of Random Sampling?
Random sampling is a widely used method for selecting a sample that is representative of a population. The following are some of the principal benefits of random sampling:
- Representativeness: In order to ensure that the sample is representative of the population, random sampling makes sure that every member of the population has an equal chance of being included in it.
- Generalization: Random sampling allows for the generalization of the findings to the population at large, which means that the results obtained from the sample can be applied to the entire population.
- Estimation and Hypothesis Testing: Random sampling allows researchers to estimate population parameters and test hypotheses, which can be useful for making inferences about the population.
- Reduction of Bias: Random sampling reduces the chance of the researcher’s own biases influencing the sample selection.
- Ease of implementation: Random sampling is relatively easy to implement and understand, making it accessible to a wide range of researchers.
- Well-established method: Random sampling is a widely accepted method for selecting a sample that is representative of a population, it has been used in many research fields, and its results are easy to interpret.
What Are the Limitations of Random Sampling?
Random sampling is a widely used and accepted method for selecting a sample that is representative of a population, but it does have some limitations. Some of the limitations of random sampling include the following:
- Sampling error: Even with random sampling, there is still a chance that the sample selected may not be perfectly representative of the population. This can lead to sampling error, which is the difference between the sample statistics and the true population parameters.
- Cost: Random sampling can be costly, especially when the population is large or widely dispersed. It can be difficult and expensive to obtain a representative sample when the population is hard to access.
- Limited sample size: Depending on the size of the population and the desired level of precision, the sample size required for random sampling can be large. This can be a limitation when resources and time are limited.
- Nonresponse bias: In some cases, individuals who are selected for the sample may not respond or may not be able to respond. This can introduce bias into the sample if the non-responders are systematically different from the responders.
- Hidden population: Sometimes, a population is hidden and hard to identify, making it difficult to obtain a random sample. For example, if trying to study a specific disease in a population, it may be hard to identify all the individuals with the disease.
It’s important to note that despite these limitations, random sampling is still considered a valid and reliable method for selecting a sample that is representative of a population, especially when used in combination with other techniques such as weighting.
Three Examples of Random Sample in Mathematics
Example 1
What is the average score on a math test for students in a certain school?
Solution
A random sample of 100 students from the school can be selected, and their test scores can be recorded and analyzed to estimate the average test score of all students in the school.
Example 2
What is the standard deviation of a certain set of data?
Solution
A random sample of 100 data points from the set can be selected, and the standard deviation can be calculated for the sample data. This can be used as an estimate of the standard deviation for the entire set of data.
Example 3
What is the probability that a certain coin is fair?
Solution
A random sample of 1000 flips of the coin can be conducted, and the number of heads and tails can be recorded. The proportion of heads and tails in the sample can be used to estimate the probability of heads for the entire population of coin flips, assuming that the coin is fair.
All images were created with GeoGebra.
