JUMP TO TOPIC
Rational Numbers|Definition & Meaning
Definition
A number is rational if it is possible to represent it as a fraction (equivalently, a ratio or division) of two integers. For example, we can write 2 as 4/2 or 2/1, so 2 is a rational number. Any number that cannot be represented in this form is called an irrational number (e.g., pi and Euler’s number e).
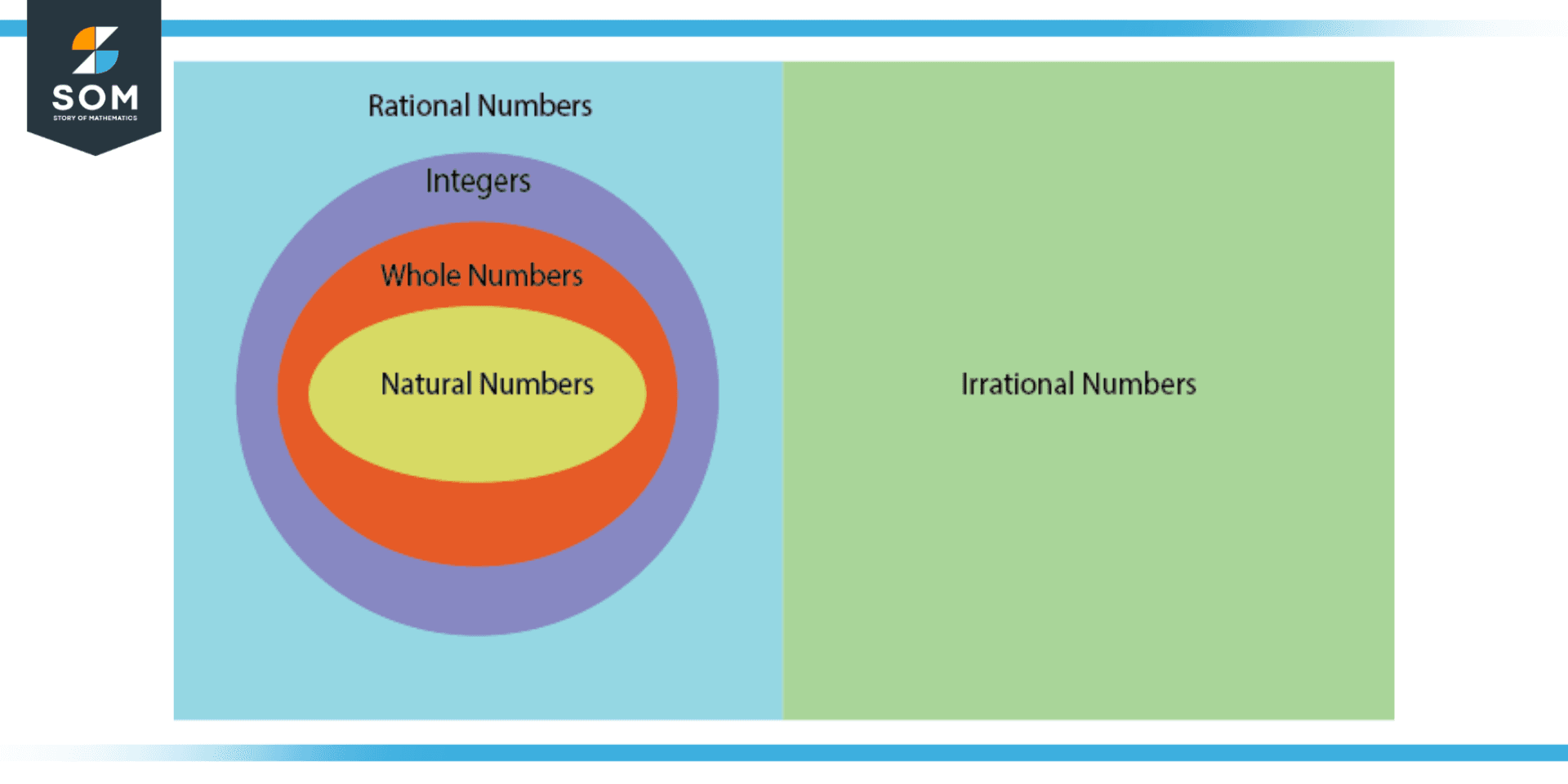
Figure 1: Diagram showing rational numbers as a set of N, W and Z.
The set of rational numbers also contains all of the integers, which can each be expressed as a ratio of two numbers where the numerator can be an integer and the denominator can be equal to 1. Rational numbers can be repeating or terminating decimals in decimal form.
The word “ratio” is where the word “rational” was first derived from. Rational numbers are therefore closely tied to the idea of fractions, which stand for ratios.
In other terms, a number would be a rational number if it can be written as a fraction in which the numerator and denominator are both integers.
All natural, whole, and integer numbers are included in the set of rational numbers. The set of rational numbers is denoted by Q.
Identification of Rational Numbers
The following attributes make it simple to recognize rational numbers:
- Rational numbers include all integers, whole numbers, natural numbers, and fractions containing integers.
- We can tell that a number is rational if its decimal form is terminating or recurring, as in the cases of 7.5 and 4.272727.
- Irrational numbers are those in which it appears that the decimals never finish or don’t repeat. Consider the number 5, which is irrational and equal to 2.2360679774997896409173.
- Checking if a number can be represented as the ratio of p/q, where p and q belong to the set of integers and q must not be equal to 0, is another method for determining whether or not a number is rational.
Terminating Decimal Numbers Are Rational
A rational number is any decimal that terminates or concludes at some point.
Consider the decimal value 0.5 as an illustration. This is a rational number since it may be changed to 1/2.
It is completely possible to transform even lengthier terminating decimal integers into fractions.
For instance, 0.0001 is a rational number since it can be written as 1/10,000.
A decimal number is, therefore, rational if its final value is reached without approximation or rounding.
Non-terminating Decimal Numbers With Indefinite Repetition Are Decimal
Rational numbers are those numbers that never end and have patterns. Since the pattern must continue forever, this is a little problematic.
Take the number 0.33333, for instance. Despite the fact that this is frequently abbreviated as 0.33, the sequence of 3s that follow the decimal point repeats indefinitely. This indicates that the number is rational and can be expressed as the fraction 1/3.
Consider using a more challenging number, such as 0.142857142857. Again, the pattern of 142857 that follows the decimal point repeats indefinitely, and the number can be expressed as the rational fraction 1/7.
There are decimal numbers, though, that never end and don’t have recurring patterns. They are not rational numbers.
Properties of Rational Numbers
A rational number will adhere to all the characteristics of the real number system because it is a subset of the real number. The following are some crucial characteristics of rational numbers:
- If we multiply, add, or subtract any two rational numbers, the outcome is always a rational number.
- If we use the same factor to divide or multiply the numerator and denominator, the answer is still a rational number.
- A rational number itself is what is obtained if we add zero to it.
- The operations of addition, subtraction, and multiplication on rational numbers are closed.
- Commutative addition and multiplication apply to rational numbers.
Commutative Property
According to the commutative law of addition:
A + B = B + A
According to the commutative property of multiplication:
AB = BA

Figure 2: Commutative property of rational numbers.
Associative Property
The associative property is followed by rational numbers while adding and multiplying. Assuming X, Y, and Z are rational, for addition:
X + (Y + Z) = (X + Y) + Z
In the case of multiplication, we have:
X (YZ) = (XY) Z

Figure 3: Associative property of rational numbers.
Distributive Property
If P, Q, and R are three rational integers, according to the distributive property, then:
P (Q + R) = (PQ) + (PR)

Figure 4: Distributive property of rational numbers.
We can apply it in the same way for multiplication over subtraction. However, remember that division is not distributive over the set of rational numbers (consider the case where the denominator becomes zero).
Irrational Numbers
Irrational numbers are any numbers that do not fit the criteria of a rational number. A decimal can be used to represent an irrational number even though it cannot be expressed as a simple fraction. After the decimal point, there are an infinite number of non-repetitive digits.
Many square roots (√2 = 1.41421356237…) and pi (π = 3.1415926536…) have digits that extend indefinitely past the decimal point. However, as they lack infinitely repeating patterns, they are regarded as irrational.
A separate set, the set of irrational numbers, does not at all constitute any of the remaining sets of numbers. Q’ represents the set of irrational numbers.
Solved Examples Using the Definition of Rational Numbers
Example 1
Assess whether 8/10, 70/1408, 25, and √7 are rational or irrational.
Solution
Since a ratio can be employed to express a rational number, which shows that it may be written as a fraction with a whole number as both the denominator and the numerator.
- Due to it being stated as a fraction, 8/10 is a rational number. Since 8/10 = 0.8.
- 70/1408 is a fraction and hence a rational number.
- As well as being rational, 25 can also be expressed as 25/1. Once more, a rational number.
- √7 has a value of 2.645751311….. Because it is non-terminating, it cannot be expressed as a fraction. Therefore, the number is irrational.
Example 2
Find three rational numbers between 2/5 and 2/3.
Solution
Let’s multiply 2/5 by 3/3 and 2/3 by 5/5. Hence, we get:
6/15 and 10/15
Since there is a sequence, the other three numbers are:
6/15, 7/15, 8/15, 9/15, 10/15
Example 3
Prove the associative property under multiplication when:
A = 8
B = 3
C = 12
Solution
Associative property under multiplication is:
A (BC) = (AB) C
8 (3×12) = (8×3) x 12
8 (36) = (24) 12
288 = 288
Hence, proved.
All images/mathematical drawings were created with GeoGebra.
