Ray|Definition & Meaning

More precisely, given two points A₁ and A₂ in space, joining them with a half-infinite line $\mathsf{\overrightarrow{A_1A_2}}$ in the direction A₁ to A₂ results in a ray if and only if it passes through the entire set of ordered collinear points both beyond A₂ {B₁, B₂, … B_n} and between A₁ and A₂ {C₁, C₂, … C_n} in that direction. Thus, the order of points along the ray would be (A₁, C₁, C₂, …, C_n, A₂, B₁, B₂, …, B_n), and we can say that it passes through all the points in space that lie in a particular direction from a defined starting point. We illustrate this in the following figure: 

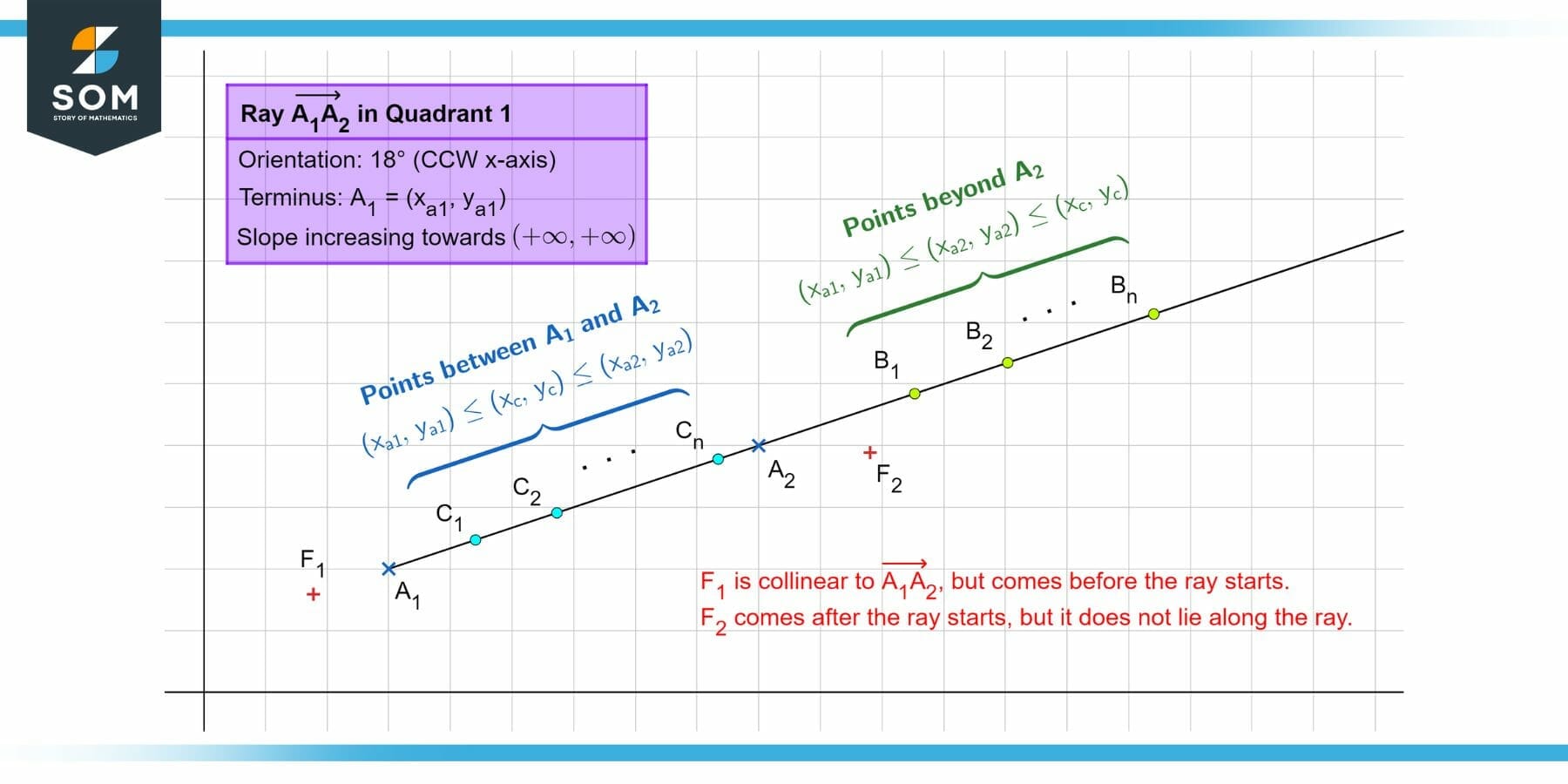
Figure 1 – A detailed illustration of a ray according to its definition.

Visualization on Graphs

Since we cannot draw an infinite line, we draw rays as a thin, finite line originating at the terminus with an arrow on the other end to indicate infinite length. This symbolization might sound familiar because we draw vectors the same way. 

While a ray has an infinite length and direction, a vector is a well-defined quantity with a finite length (magnitude) and direction. Therefore, much like a line segment, a vector has both a starting and an endpoint – very different from a ray!

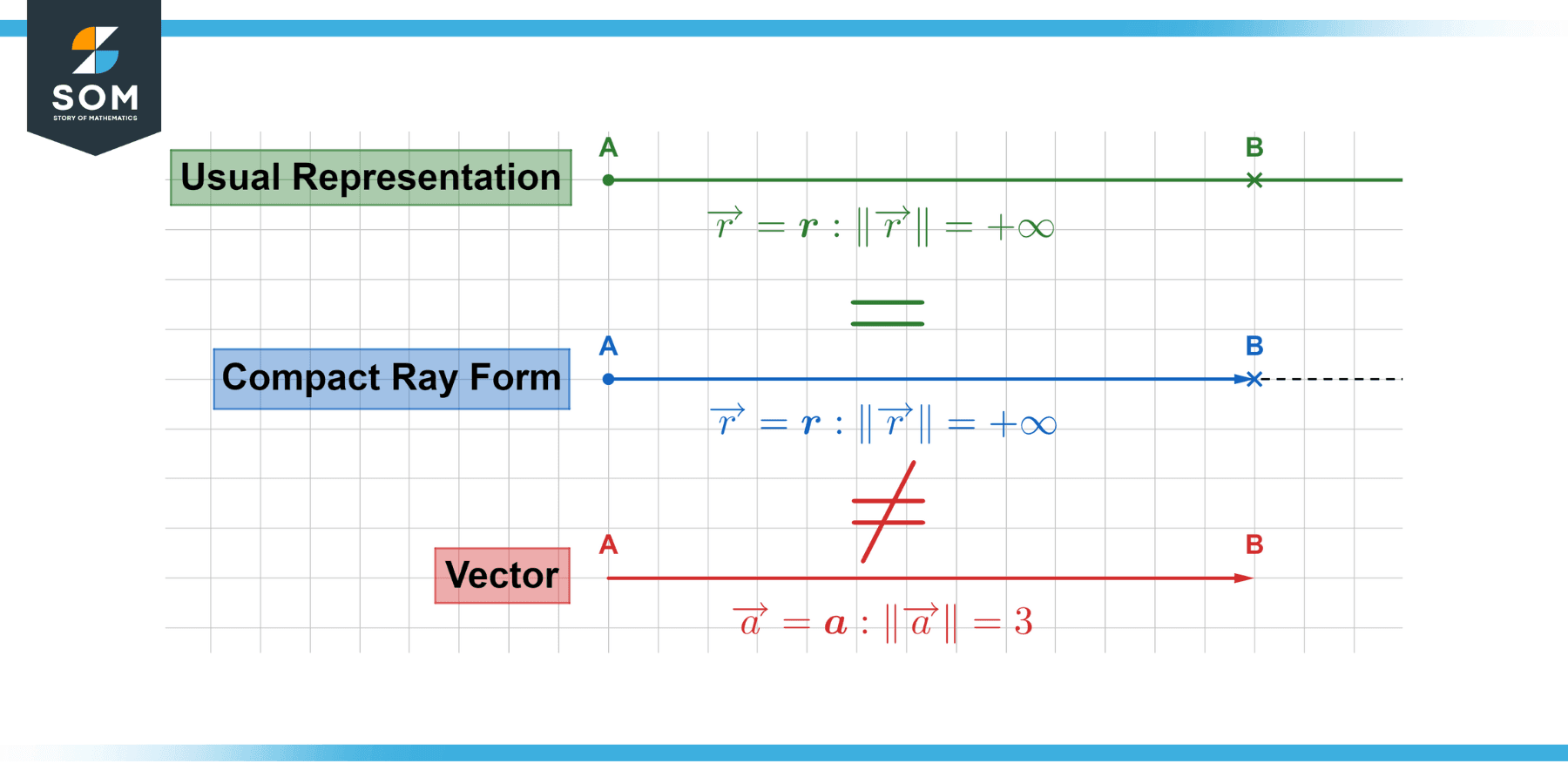
Figure 2 – The difference between the compact notation of a ray and a vector.

Intuition and Relationship With Lines and Line Segments

A line segment has a finite length with two endpoints, say A and B, so it passes through all the points between A and B. On the other hand, a line is infinite on both ends (has no endpoints) and passes through all the points (x, y) in space that satisfy the equation of a line: 

y = mx + c 

Where m is the slope and c is the y-intercept of the line. In other words, if you extend a line segment infinitely beyond its endpoints, you get a line. 

Now, you can think of a ray as a line, but instead of extending infinitely in two directions, it does so in only one. Equivalently, you can think of it as a line segment with only one endpoint and the length extending to infinity in the direction of the segment’s other endpoint. Thus, if the terminus of a ray is (p, q), then the equation of the line represents the ray:

(y – q) = m(x – p), where x $\geq$ p and y $\geq$ q

And we can find the direction of the ray as an angle:

$\theta$ = arctan(m)

A geometrical ray has only one point: the terminus. We use either angles or another point in space to specify the direction. 

Point-finding on Rays

There are two steps to the process. The first step is to check whether the candidate point’s coordinates (x_c, y_c) satisfy the ray’s slope-terminus relationship. Assuming the ray’s terminus is (p, q) and the slope is m, we have the following four cases:

1. If m > 0 and ray points towards ($+\infty$, $+\infty$), the point must satisfy: x_c $\geq$ p, y_c $\geq$ q.
2. If m > 0 and ray points towards ($-\infty$, $-\infty$), the point must satisfy: x_c $\leq$ p, y_c $\leq$ q.
3. If m < 0 and ray points towards ($+\infty$, $-\infty$), the point must satisfy: x_c $\geq$ p, y_c $\leq$ q.
4. If m < 0 and ray points towards ($-\infty$, $+\infty$), the point must satisfy: x_c $\leq$ p, y_c $\geq$ q.

If the point (x_c, y_c) passes the first check, we must perform the second check. That is, does the point (x_c, y_c) satisfy:

(y_c – q) / (x_c – p) = m

Here, m is the known value of the slope. If the above equality holds, the point has passed both checks, and we can say that the point (x_c, y_c) lies on the ray.  

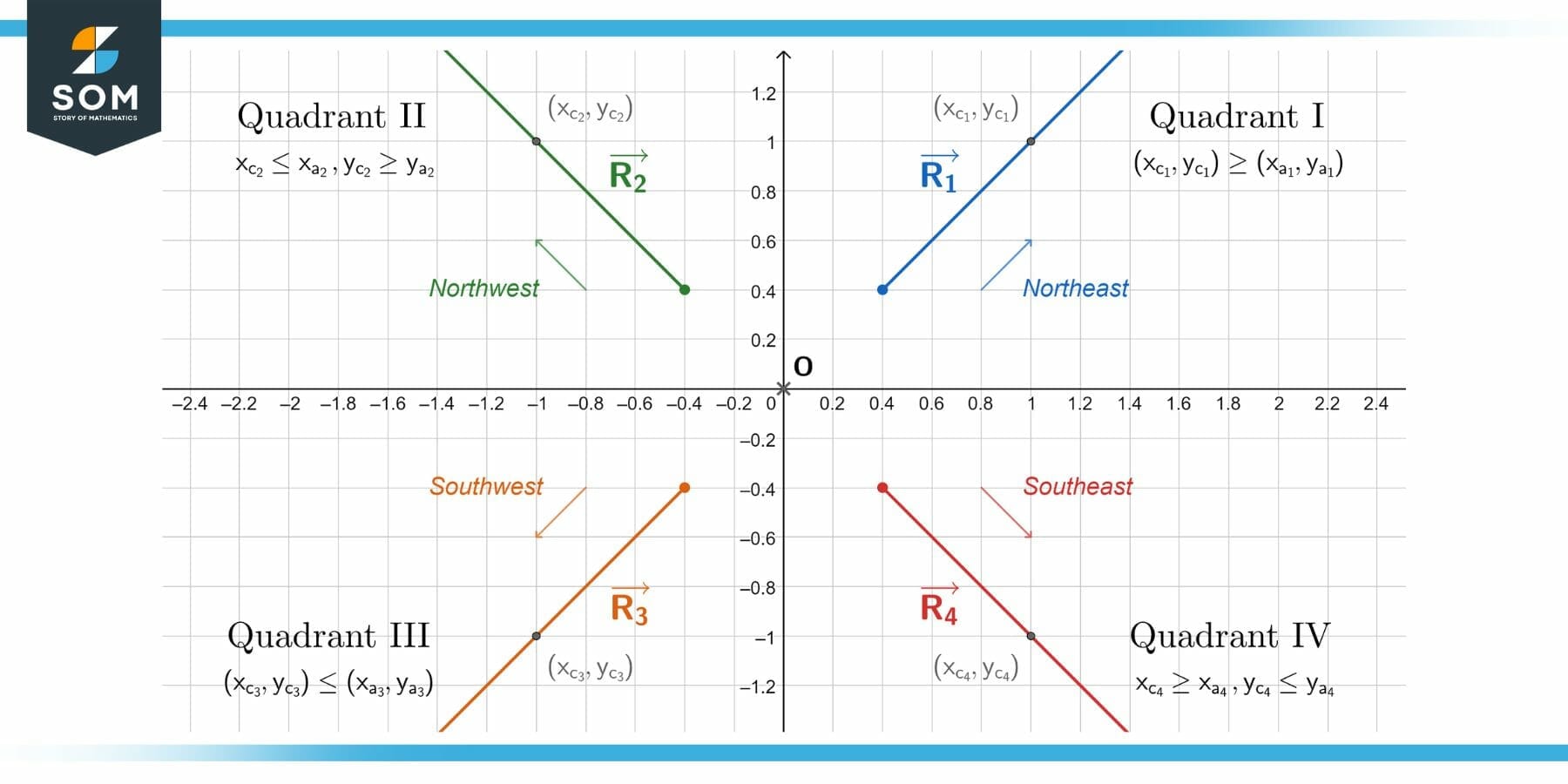
Figure 3 – The first step in finding points on rays is to relate the ray direction to a quadrant.

A ray centered at the origin towards the first quadrant points to ($+\infty$, $+\infty$), while one towards the third points to ($-\infty$, $-\infty$). Note that this is not always true for rays not centered at the origin. In that case, the way to go is to check for one of the combinations of ($\pm\infty$, $\pm\infty$).

A Solved Numerical Problem on Rays

Example 1

Given the equation of a line y = 3x + 2, find a ray parallel to it with a terminus (3, 1) pointing towards ($+\infty$, $+\infty$).

Solution

Method 1: To find a ray parallel to the line, we simply need the angle $\boldsymbol\theta$ of the line.

$\boldsymbol\theta$ = arctan(3) = 71.565${}^{\boldsymbol{\circ}}$

Now, place a protractor on the terminus (3, 1) and draw a line in that direction, and you are done! 

The second method involves finding another point on the ray and joining the terminus with it. We can proceed in one of two ways. Remember that the slope is increasing towards the northeast, so all choices of x and y should be greater than the terminus’ coordinates to pass the first check from earlier.

Let subscript ‘l’ represents the points on the line, and subscript ‘r’ represents the points on the ray.

Method 2.1: Use the equation of slope:

m = (y_r2 – y_r1) / (x_r2 – x_r1)

Substitute m = 3, x_r1 = 3, y_r1 = 1, and one of x_r2 $\geq$ 3 = 4 or y_r2 $\geq$ 1 = 2. Suppose we set x_r2 = 4. Then we need to solve for y_r2:

 y_r2 = m(x_r2 – x_r1) + y_r1

y_r2 = 3(4 – 3) + 1 = 3 + 1 = 4

y_r2 = 4

Therefore, we get the second point on the ray as:

(x_r2, y_r2) = (4, 4)

Method 2.2: Since the ray is parallel to the line, their points have a specific offset. To find it, we need to plug x_l1 = 3 or y_l1 = 1 into the equation of the line and find the difference between the resulting coordinates and (3, 1). Assuming we plug in x_l1 = 3, then y_l1:

y_l1 = 3(3) + 2 = 11

(x_l1, y_l1) = (3, 11)

offset = (x_l1, y_l1) – (x_r1, y_r1) 

offset = (3, 11) – (3, 1) = (0, 10)

Evidently, for the same x-coordinate, the y-coordinate is offset by 10. It follows that all other points on the ray and the line (for the same x) are shifted by 10 in the y-direction!

For another point on the line that also lies on the ray, choose x_l2 $\geq$ 3 or y_l2 $\geq$ 1. Say we pick x_l2 = 4, then:

y_l2 = 3(4) + 2 = 14

(x_l2, y_l2) = (4, 14)

Therefore, the coordinates of the point on the ray are:

(x_r2, y_r2) = (x_l2 – 0, y_l2 – 10) = (4 – 0, 14 – 10) = (4, 4)

(x_r2, y_r2) = (4, 4)

We get the same answer from both methods. Joining the terminus to this point gives us the ray! We draw this below:

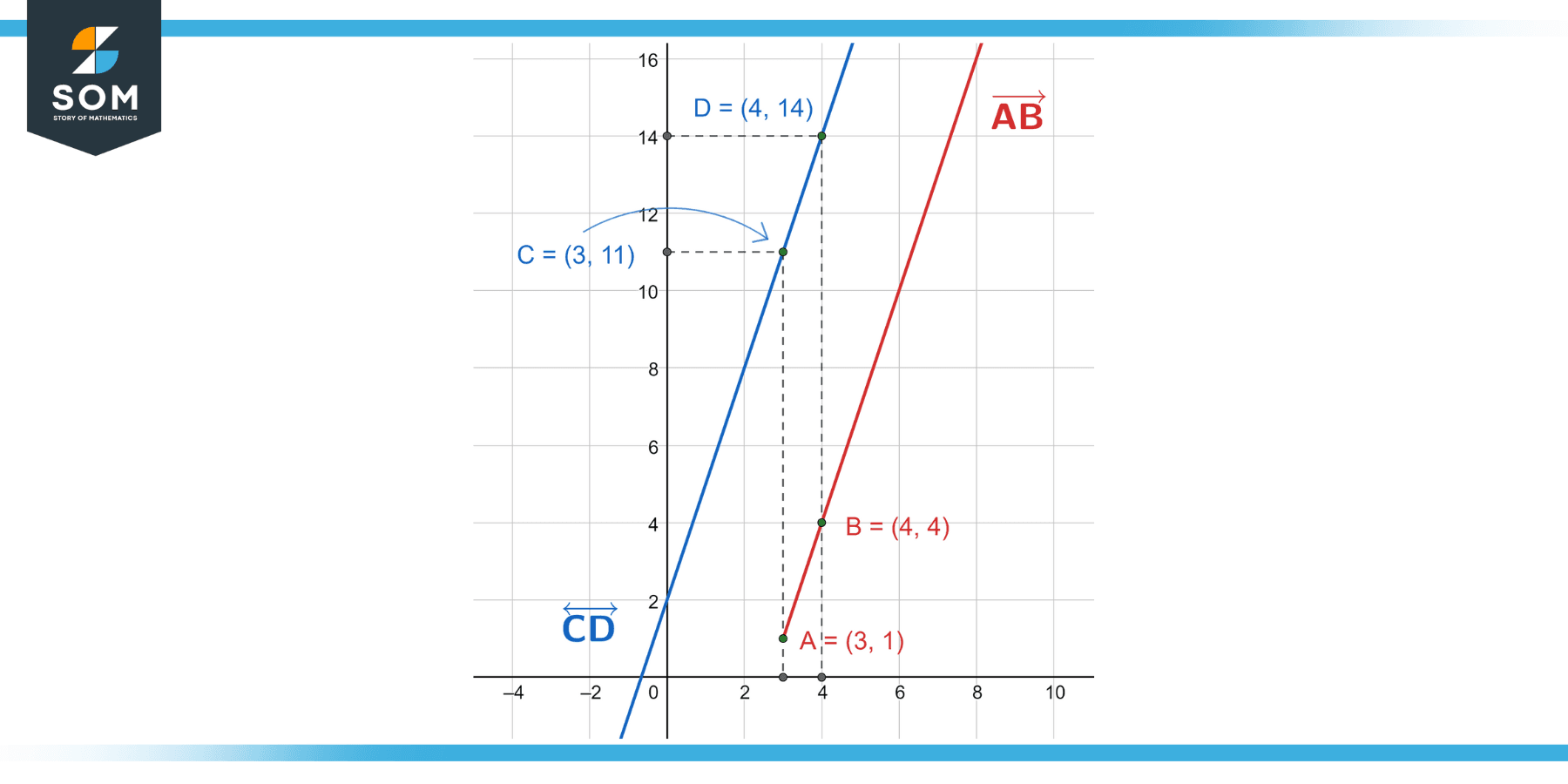
Figure 4 – The ray AB (in red) from the equation of the line CD (in blue). Notice that the x and y intercept do not exist for the ray.

All graphs/mathematical figures were created with GeoGebra.

Rational Number Definition < Glossary Index > Real Number Definition