JUMP TO TOPIC
Real Number|Definition & Meaning
Definition
All non-imaginary numbers are called real numbers. Therefore, the set of real numbers includes all other sets except imaginary numbers, i.e., rational, irrational, integer, whole, and natural numbers are all subsets of real numbers.
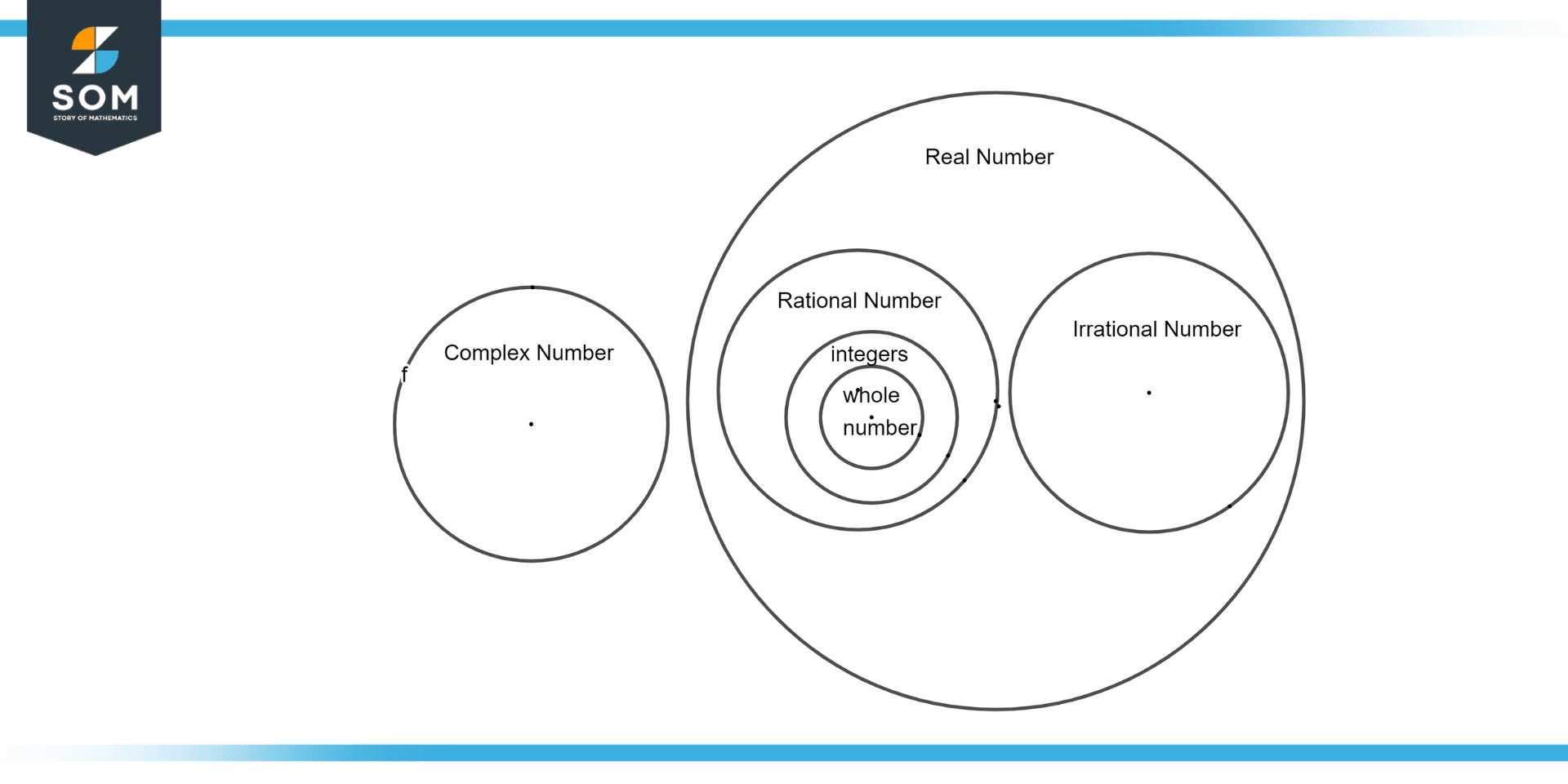
Figure 1 – Real Numbers
Figure 1 illustrates the graphical representation of real numbers.
The union of rational and irrational numbers is called real numbers. They are represented by the letter $\textbf{R}$ and can be either positive or negative. This category includes all-natural integers, decimals, and fractions.
Integers that can be expressed as fractions p/q are called rational numbers. The fraction has a numerator of “p” and a denominator of “q,” where “q” is not equal to zero. Natural numbers, whole numbers, decimals, and integers can all be rational numbers.
The group of real numbers known as irrational numbers is a set of numbers that cannot be represented as a fraction of the form p/q. In this form, p and q must be integers, and q must be non-zero (q ≠ 0).
The foregoing informal explanations of real numbers are insufficient to guarantee the accuracy of the theorem proofs that include real numbers.
Real analysis, the study of real functions, and real-valued sequences are all built on the awareness that a better definition was required and the invention of one. This was a significant mathematical development of the 19th century.
The unique Dedekind-complete ordered field of real numbers is now defined axiomatically. Cauchy sequences (of rational numbers), Dedekind intersections, and equivalence classes of infinitesimal representations are other common definitions of real numbers. All these definitions are the same because they all conform to the axiomatic definition.
Properties of Real Number
The closure, associative, commutative, and distributive properties of the set of real numbers are satisfied, much as those of the sets of natural and integer numbers.
Closure Property
According to the closure property, the result of adding and multiplying two real numbers is always a real number. The following is how R’s closure property is expressed: If a, b ∈ R, a + b ∈ R and ab ∈ R.
Associative Property
Even when the order of the numbers is altered, the sum or product of any three real numbers stays the same. Following is a description of R’s associative property: If a,b,c ∈ R, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c
Commutative Property
Even after switching the numbers’ order, the total and product of two real numbers stay the same. The following sentence expresses R’s commutative property: If a, b ∈ R, a + b = b + a and a × b = b × a.
Distributive Property
Real numbers are distributive. Hence, they are real numbers. a (b + c) = (a$\times$b) + (a$\times$c) is the distributive property of multiplication over addition, whereas a (b – c) = (a$\times$b) – (a$\times$c) is the distributive property of multiplication over subtraction.
Differences Between Real Numbers and Integers
Rational, irrational, whole, and natural numbers are all examples of real numbers. $\textbf{R}$ is the symbol used to represent real numbers. A distinct actual number is displayed at each place on the number line. Fractions and the decimal system are regarded as real numbers.
Negative, positive, and zero numbers are all examples of integers. Integers are represented by the letter $\textbf{Z}$. On a number line, integers are represented only by whole numbers and negative values. Fractions and decimals are excluded from integers.
Real Line
The points on an infinitely long line known as the number line or the real line, where the points corresponding to integers (…, 2, 1, 0, 1, 2,…) are evenly spaced, can be thought of as real numbers.
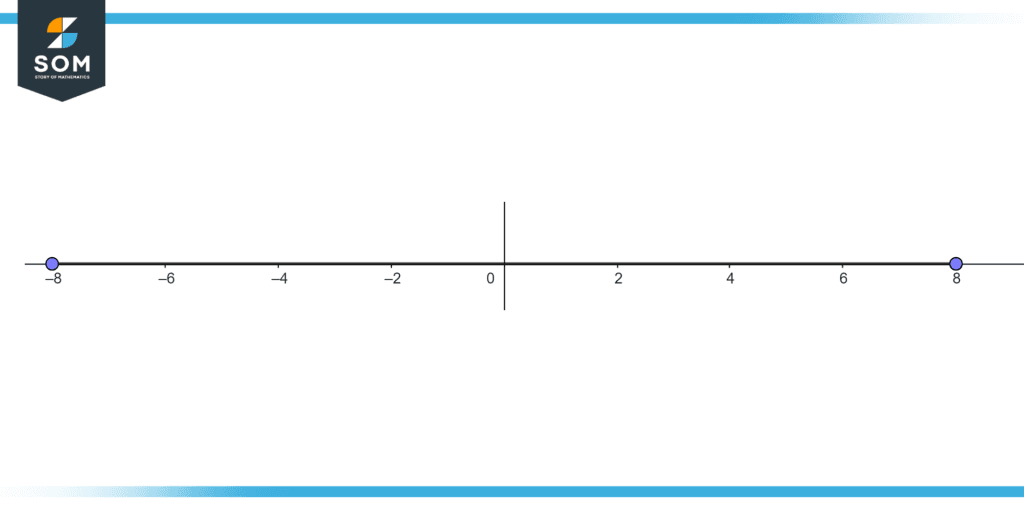
Figure 2 Real line
Figure 2 illustrates the real numbers on a real line from -8 to 8.
Applications of Real Numbers
Most physical variables, including position, mass, speed, and electric charge, as well as physical constants, such as the universal gravitational constant, are represented in the physical sciences by real numbers.
Real measurements of physical quantities are of finite precision, but fundamental physical theories such as classical mechanics, electromagnetism, quantum mechanics, general relativity, and the standard model are actually mathematical structures, usually smooth is described in a simple manifold or Hilbert space based on real numbers.
Since real numbers have several topological qualities that are a technical annoyance, the Baire space is employed as a substitute for them in set theory, more especially descriptive set theory. “Reals” are the components of Baire space.
The Zermelo-Fraenkel axiomatization of set theory is most frequently used to formalize real numbers. However, other mathematicians also investigate real numbers using different logical mathematical foundations. In particular, constructive mathematics and reverse mathematics both study real numbers.
The hyper-real numbers, created by Edwin Hewitt, Abraham Robinson, and others, add infinitesimal and infinite numbers to the set of real numbers, allowing for the construction of infinitesimal calculus in a manner that is more in line with the original intuitions of Leibniz, Euler, Cauchy, and others.
Since finite computers are unable to directly store infinite amounts of digits or other infinite representations, electronic calculators and computers cannot work on arbitrary real numbers. Furthermore, they typically don’t even work with random, difficult-to-manipulate actual numbers.
Instead, computers commonly use floating-point numbers, which approximate objects with finite accuracy and resemble scientific notation. The amount of data storage space allotted for each number, whether it be represented as a fixed-point, floating-point, arbitrary-precision number, or in another way, determines the possible accuracy.
Most scientific calculations employ binary floating-point arithmetic, which frequently has a 64-bit representation and a precision of about 16 decimal digits.
Some Examples of Real Numbers
Example 1
Illustrate the real numbers from one to seven on real line.
Solution
Draw a line from one to seven with each digit to be equally spaced as illustrated in figure 3. The line is known as real line as real numbers are illustrated on the line.
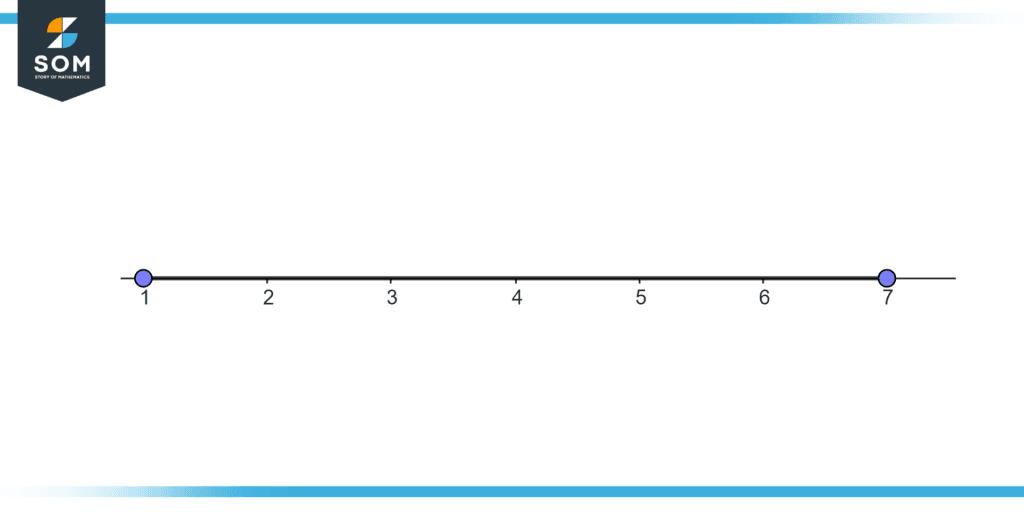
Figure 3 Real Numbers on a Real line
Example 2
What should be multiplied by 3.25 so this term will be equal to one.
Solution
We can write 3.25 as:
\[ \dfrac{325}{100} \]
If we multiply it with the reciprocal, then the answer will be equal to one.
\[ \frac{325}{100} \times \frac{100}{325} = 1 \]
All the terms will cancel out the answer will be one.
All images were created using GeoGebra.
