Rectangle|Definition & Meaning

What Is a Rectangle? 

A polygon having four sides or 4 corners are called a rectangle. If the edge-to-edge distance of all the sides of a polygon is equal in length, then the formed shape is known as a square. Whereas a rectangle has two pairs of equal-length sides, and the equal sides are opposite to each other, which differentiates it from a square.

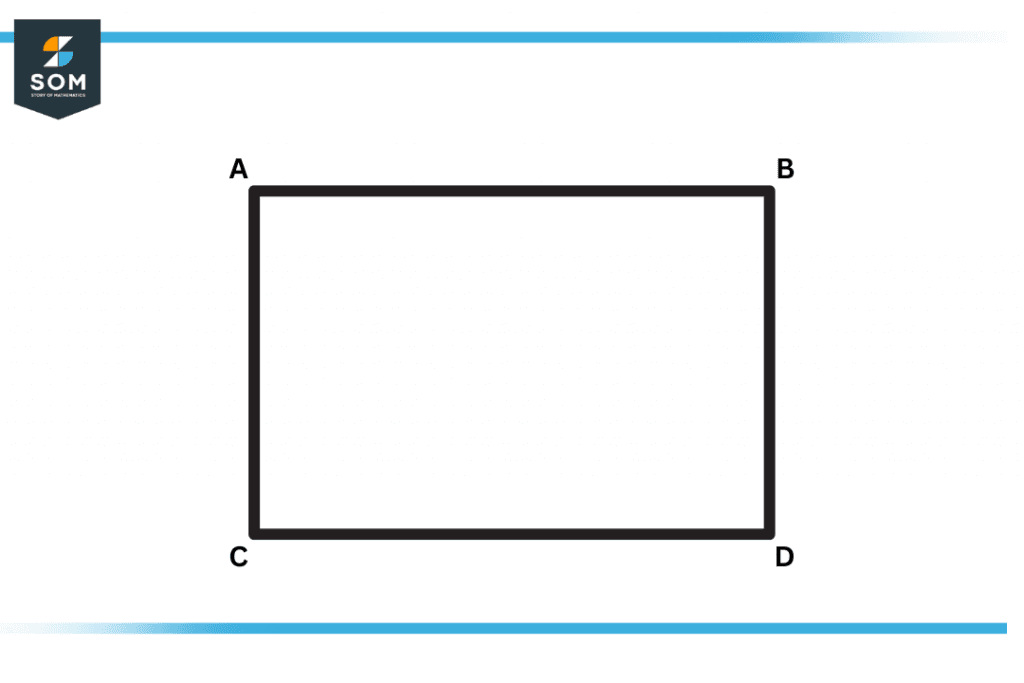
Figure 1 – ABCD is the rectangle where AB is the length and AC is the width.

A rectangle is a two-dimensional shape, which means it can not be transformed into a 3D surface. In 3 dimensional geometry, a rectangle is sometimes referred to as a cube. All the inner angles of a rectangle are equal in measure of 90$^{\circ}$. Since it is constructed in two dimensions, it is illustrated by two dimensions, length(L) and width(W).

Diagonals of a Rectangle

The line segment that begins from one vertex and ends at the opposite non-adjacent vertex is known as a diagonal. A rectangle has two diagonals that bisect each other at their point of intersection. Both diagonals are congruent and equal in length. They are not mutually perpendicular. A diagonal divides the rectangle into two right-angled triangles.

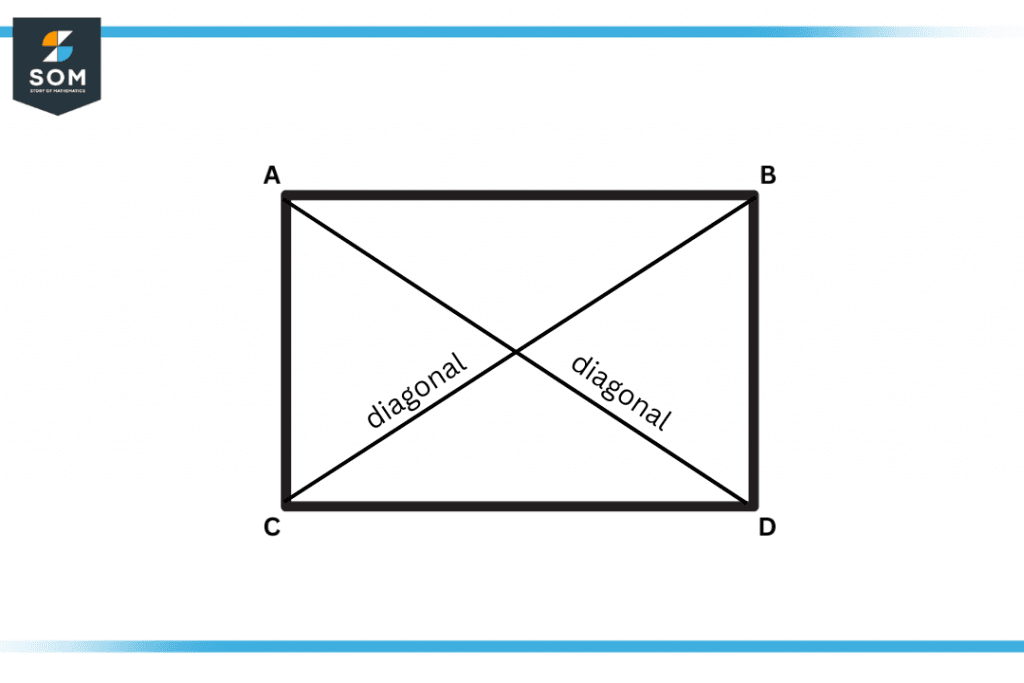
Figure 2 – Diagonals of a Rectangle

Finding the Length of a Diagonal

Consider the right angle triangle ABC, diagonal BC is the hypotenuse, AB (length) is the base, and AC (width) is the perpendicular of the triangle.

Let d represent the diagonal, l represents the length, and w represent the width. Then, by using Pythagoras’ theorem, we have

Diagonal² = length² + width²

d² = l² + w²

d = $\sqrt{l^2 + w^2}$

Let’s take a look at how to find the length of diagonals of a rectangle having two sides of 10cm in length and the other two of 6cm in length. By using the formula,

d = $\sqrt{l^2 + w^2}$

= $\sqrt{10^2 + 6^2}$

= $\sqrt{100 + 36}$

= $\sqrt{136}$

d = 11.6 cm

Therefore, the length of both diagonals is 11.6cm.

Properties of Rectangle 

Following are the properties of a rectangle

• A rectangle is a quadrilateral.
• It has 4 sides, 4 angles, and 4 vertices.
• Opposite sides of a rectangle are equal.
• Diagonals of a rectangle bisect each other.
• The length of the diagonals is equal.
• Each angle of the rectangle is 90 degrees.
• If you sum up all the interior angles, the result would be 360 degrees.
• The longer side of the rectangle is its length.
• The shorter side of the rectangle is its width.

3D Rectangle

A 3-dimensional rectangle is called a rectangular prism and cuboid. It has 6 faces, 12 edges, and 8 vertices.

Area of Rectangle 

The area of the rectangle is the entire region surrounded by the rectangle’s boundaries in a 2-dimensional plane. It is the product of length and width. The area occupied by rectangular-shaped objects such as a television, blackboard, door, refrigerator, etc., can easily be calculated by utilizing the formula for the area of a rectangle:

Area of rectangle = length * width

Consider an example of a television whose length is 42 inches and width is 20 inches. To figure out the exact area of a rectangle, we use the following formula,

Area = length * width

= 42 * 20

= 840 inch²

The Perimeter of a Rectangle

The perimeter of a rectangle is the path or distance covered by the boundary of the rectangle in a 2-dimensional plane. If two adjacent sides of a rectangle are summed up, we get the perimeter of a rectangle, which can be found using the mathematical formula given below,

Perimeter of rectangle = length + length + width + width

= 2*(length) + 2*(width)

= 2(length + width)

Consider an example of a gardener who wants to find out how much wire would be required to put a fence around his garden. The length of the garden is 15 feet, and its width is 6 feet.

The answer to this problem can be found by calculating the perimeter of the garden as follows:

Length = 15 feet

Width = 6 feet

Perimeter = 2(length + width)

= 2(15 + 6)

= 2(21)

= 42 feet

Hence, 42 feet of wire would be required to put a fence around the garden.

Quadrilateral

A quadrilateral is a four-sided plane closed figure. It has four angles and four vertices. It is a (four-sided) polygon also known as a tetragon. The total measurement of all the interior angles comes out to be 360 degrees.

A quadrilateral is a combination of two Latin words, where Quadri stands for four, and lateral is described as sides. Hence, the name itself gives the description of this plane figure.

A rectangle is a type of quadrilateral. Some other types of quadrilaterals are square, parallelogram, rhombus, trapezium, and kite.

Square

A Square is a quadrilateral, but it differs from a rectangle as all of its sides are equal in length. Like a rectangle, a square has four equal angles of 90 degrees each. Diagonals of a square cross each other at a common point that has a 90-degree angle, thus bisecting each other perpendicularly.

Parallelogram 

A parallelogram is a quadrilateral. It is like a rectangle, but its diagonals are unequal. Its opposite sides are parallel and equal. Diagonals bisect each other at the midpoint and shape two congruent triangles. A parallelogram has opposite equal angles.

We can say that a rectangle possesses all the mathematical properties of a parallelogram, but a parallelogram does not have all the properties of a rectangle. So a rectangle is a parallelogram, but a parallelogram may not be a rectangle.

 Rhombus 

A rhombus is a quadrilateral having all four sides equal, opposite sides parallel, and opposite angles equal. Diagonals of a rhombus cross each other at a common point that has a 90-degree angle, thus bisecting each other perpendicularly.  All squares are rhombus, but the converse may not be true.

Trapezium 

A trapezium is a combination of parallel and non-parallel sides. A quadrilateral having only one pair of non-adjacent parallel sides and having the other two as non-parallel sides is a trapezium. The sides that are parallel to each other are known as bases, whereas the other two non-parallel sides are known as legs. A parallelogram is a trapezium but a trapezium is not a parallelogram.

Kite 

A kite is a four-sided figure, just like a tilted parallelogram but with two pairs of sides having equal lengths. If we draw the diagonals of a kite, they will behave just like a normal rectangular diagonal by intersecting each other at right angles.

The interior opposite angles of a kite are obtuse and equal in measure.

Solved Examples Involving Rectangular Shapes

Example 1

Find the length of a rectangle whose area is 400 feet² and whose width is 16 feet.

Solution

Given:

Area = 400 feet²

Width = 16 feet

Length = ?

As we know that:

area = length * width

Putting the values of area and length in the above formula, we get:

400 = length * 16

400/16 = length

25 feet = length  

Length = 25 feet

Therefore, the rectangle has an area of 400 feet and a width of 16 feet, has a length of 25 feet.

Example 2

A rectangular prism has a length of 20 inches and a width of 15 inches. Find the area and perimeter of the prism.

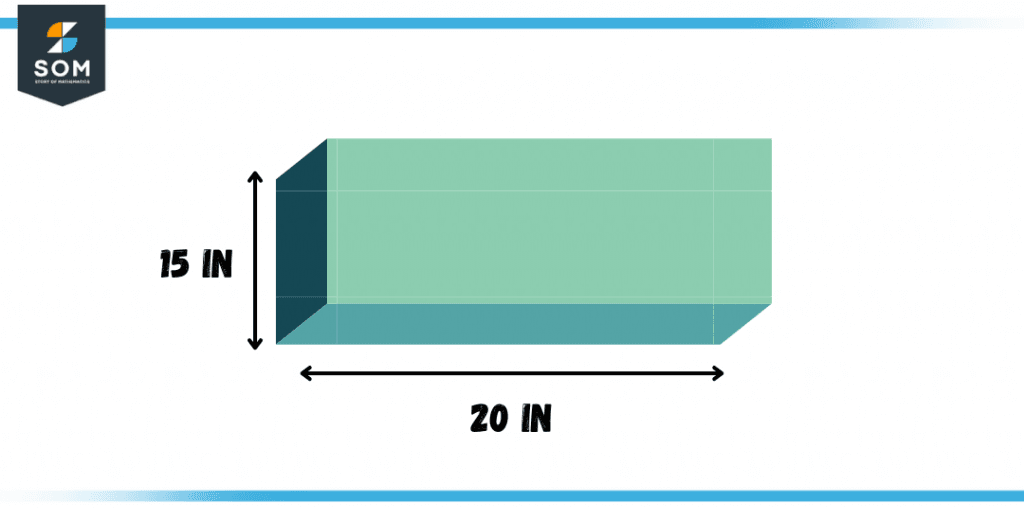
Figure 3 – Example of a Rectangular Prism

Solution

Given:

Length = 20 inches

Width = 15 inches.

Area =? ; Perimeter =?

For area, we have the formula:

Area = Length * Width

= 20 * 15

= 300 inches²

Now for perimeter, the formula is:

Perimeter = 2(length + width)

= 2(20 + 15)

= 2(35)

= 70 inches 

Therefore, the rectangular prism has an area of 300 inches² and a perimeter of 70 inches.

All images were created with GeoGebra.

Real Number Definition < Glossary Index > Rectangular Prism Definition